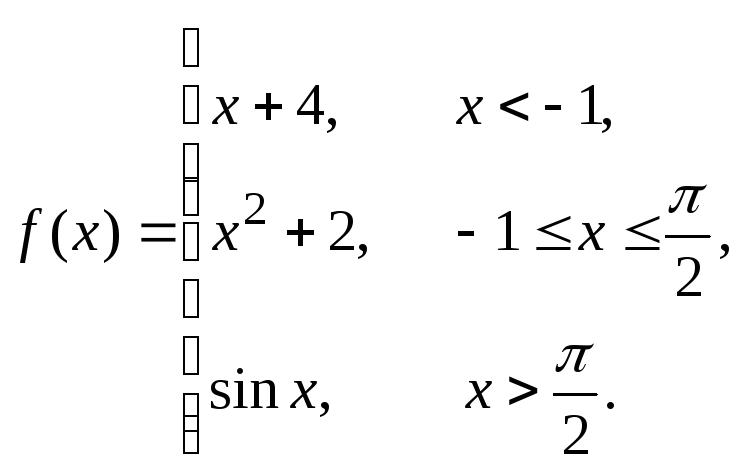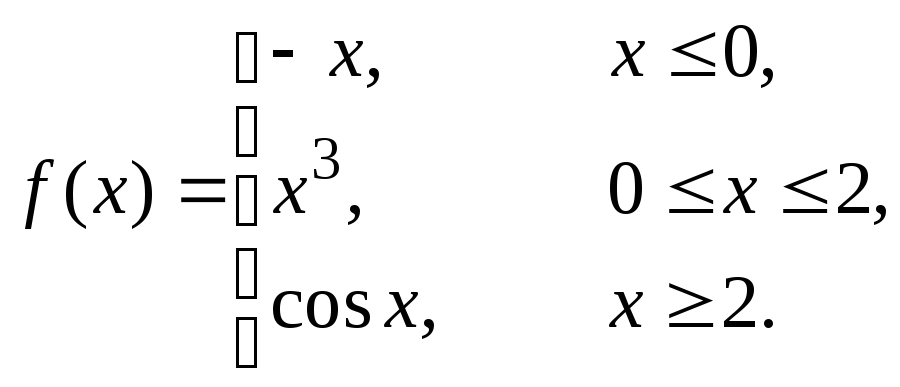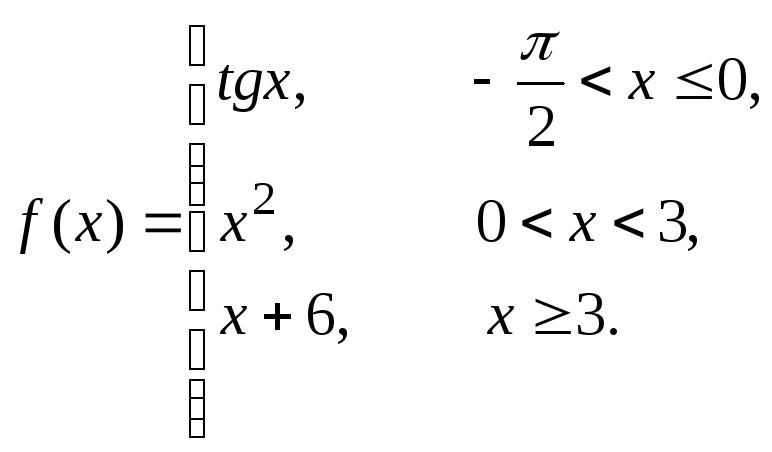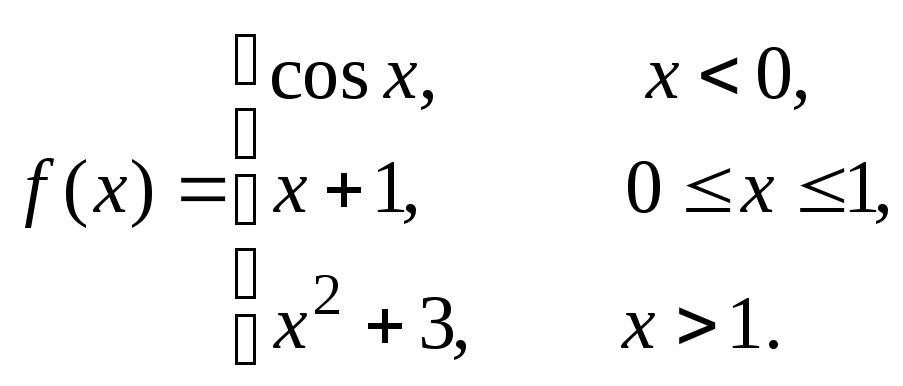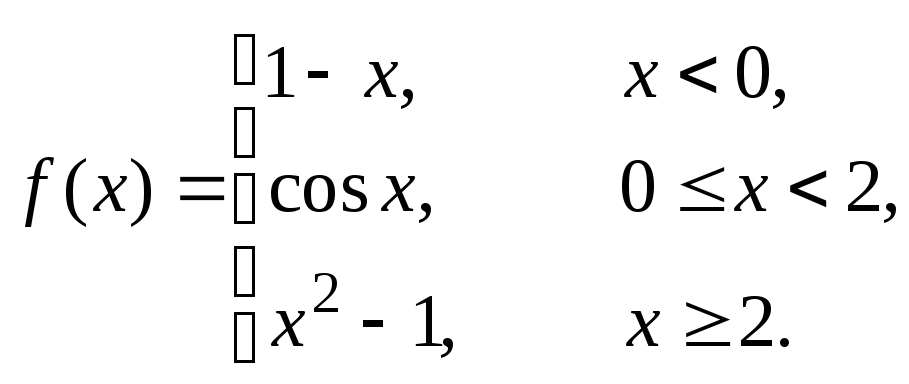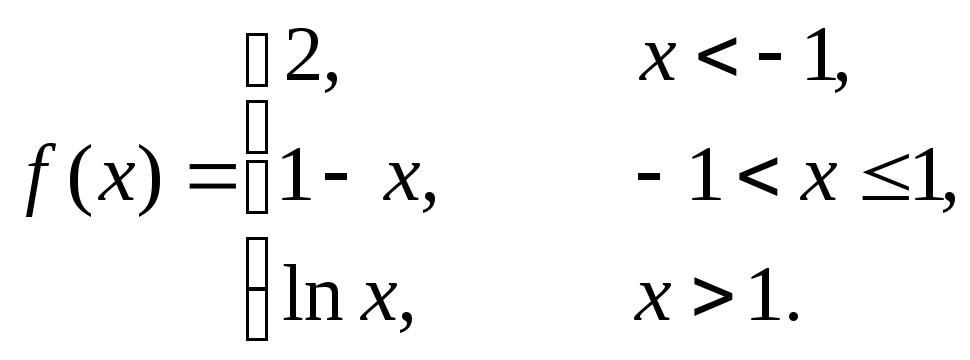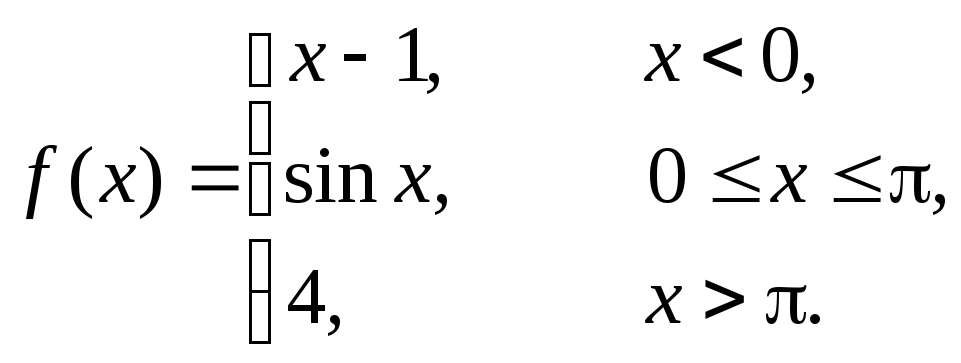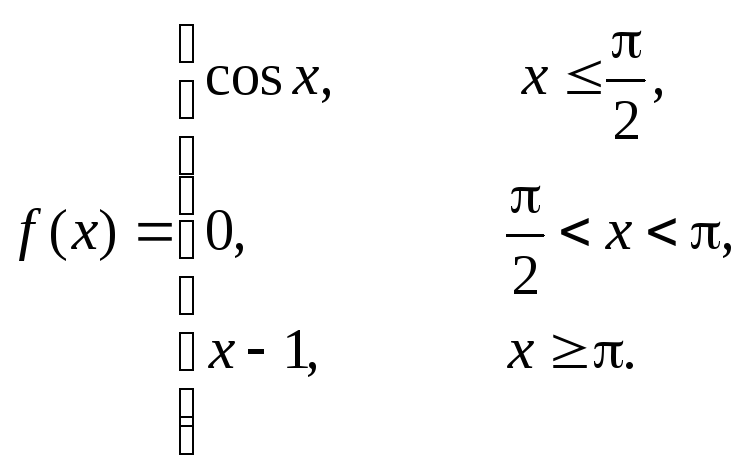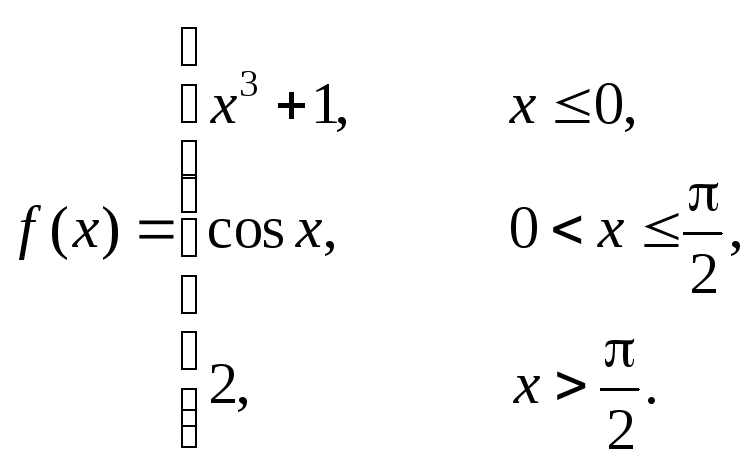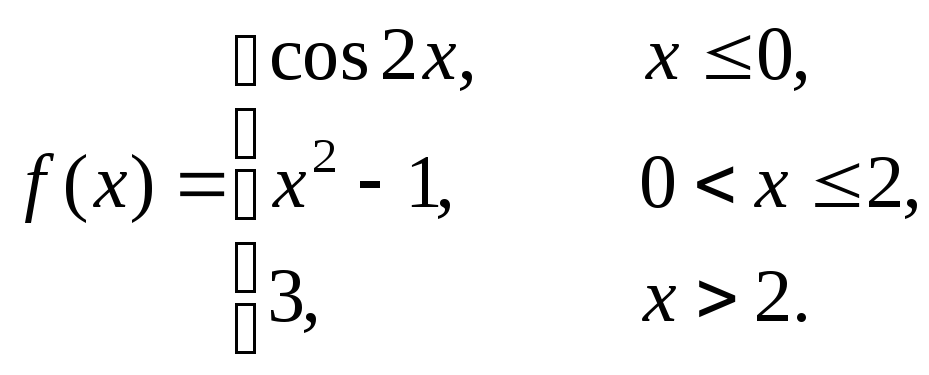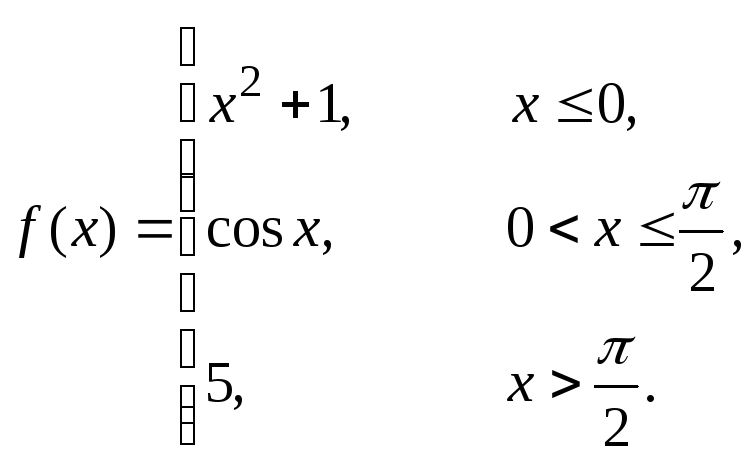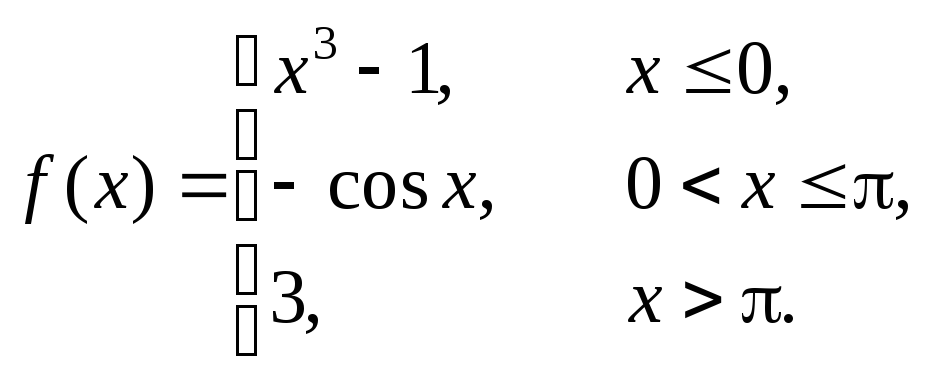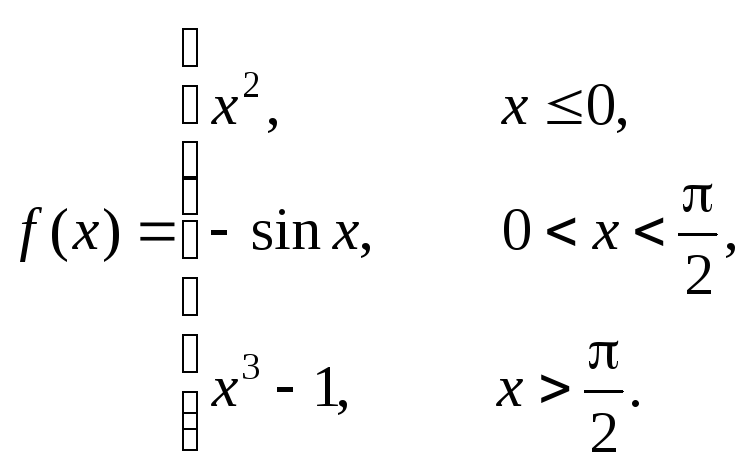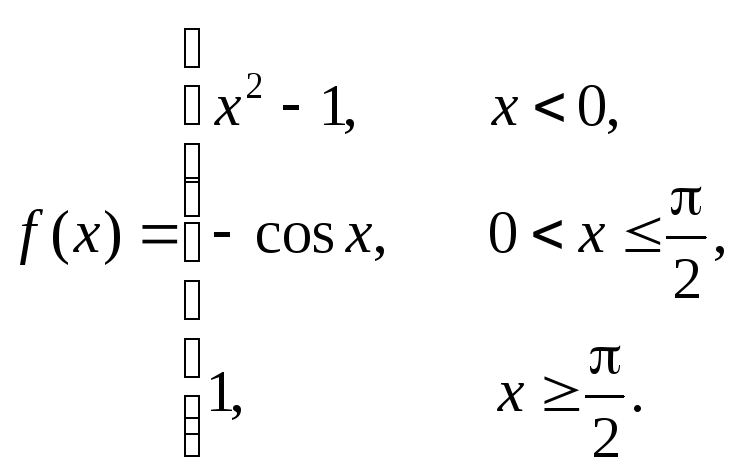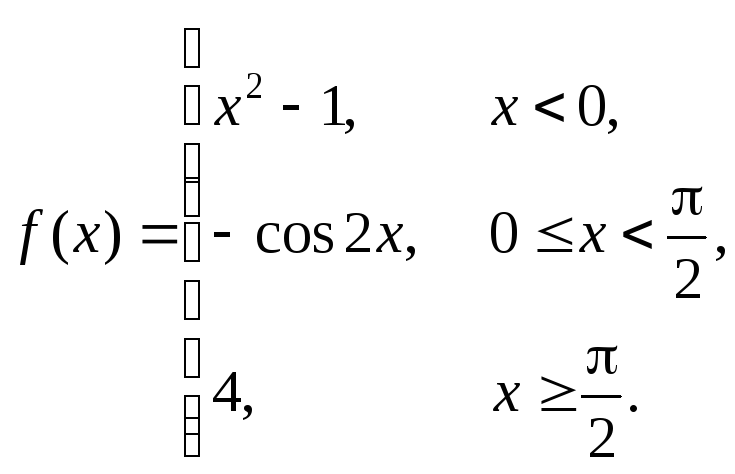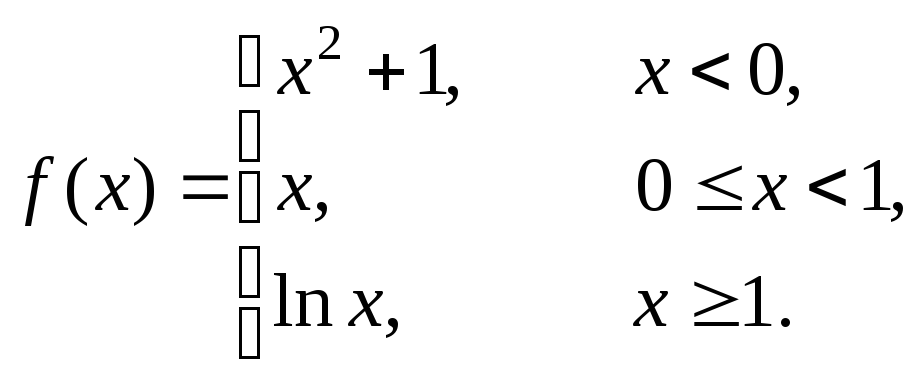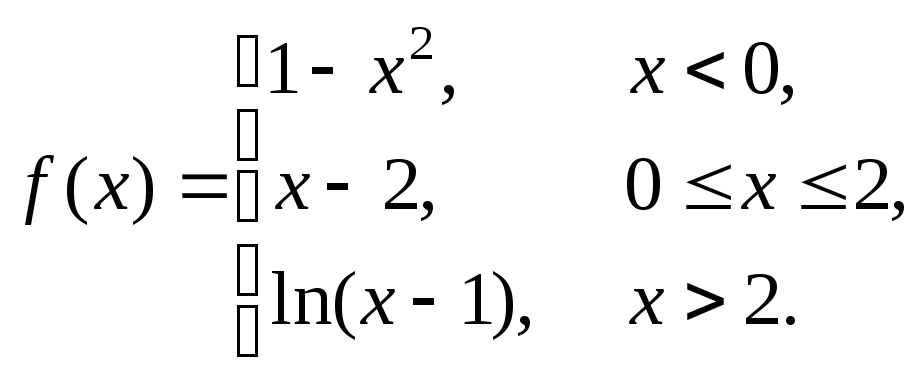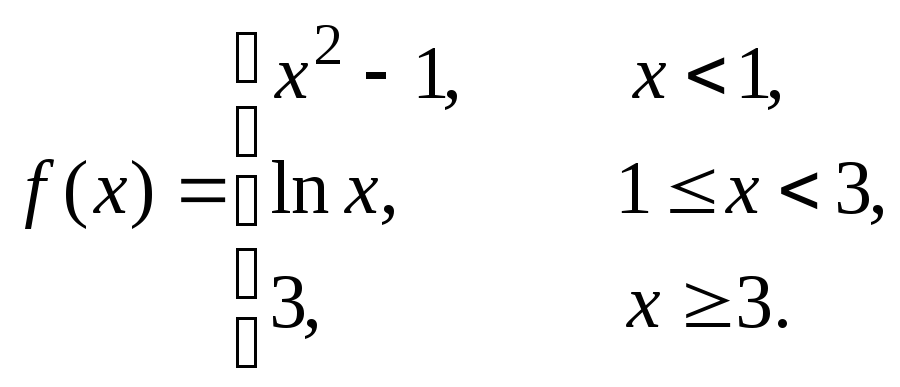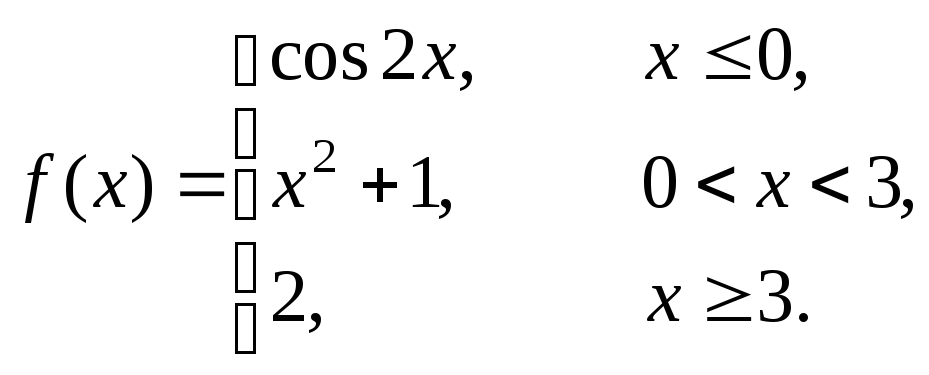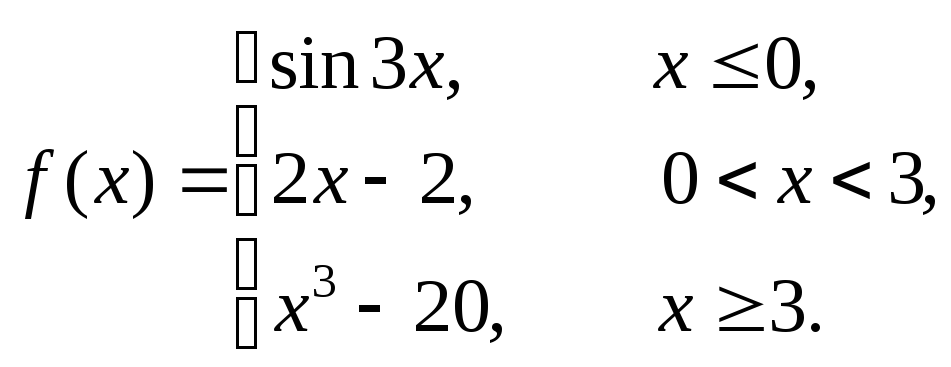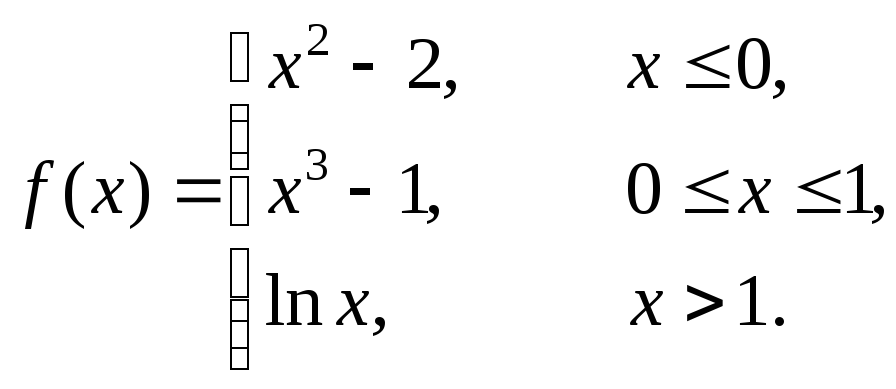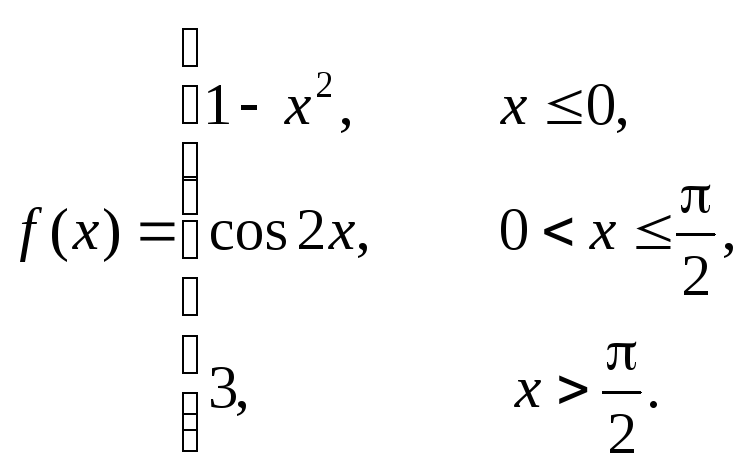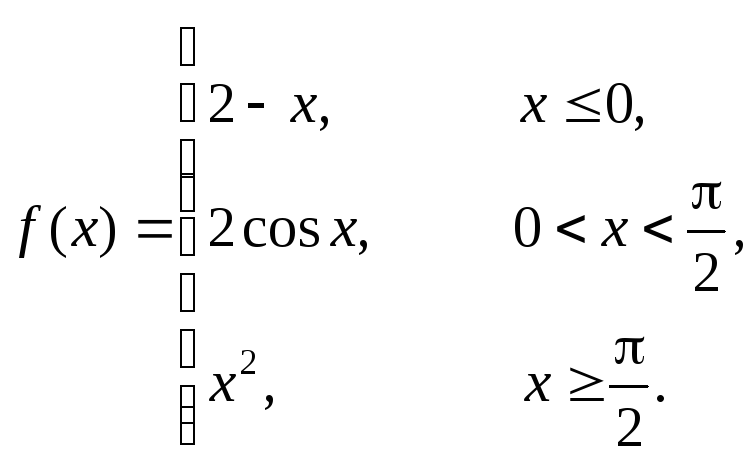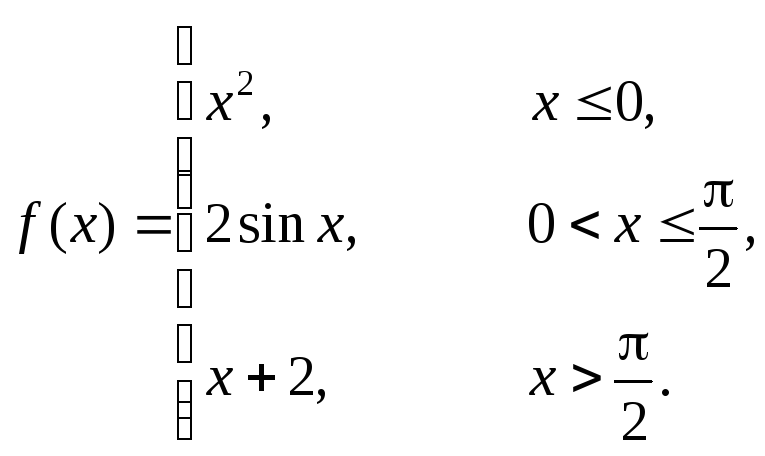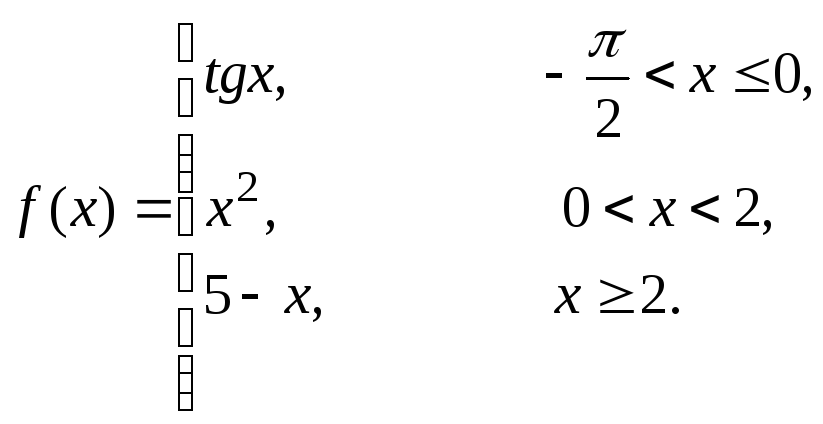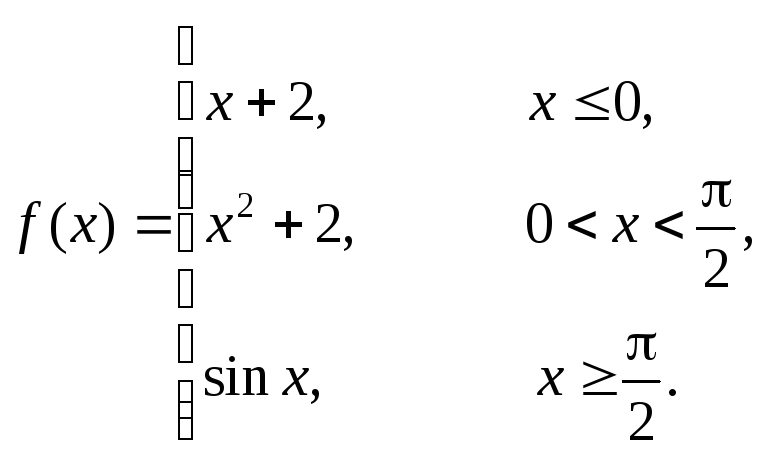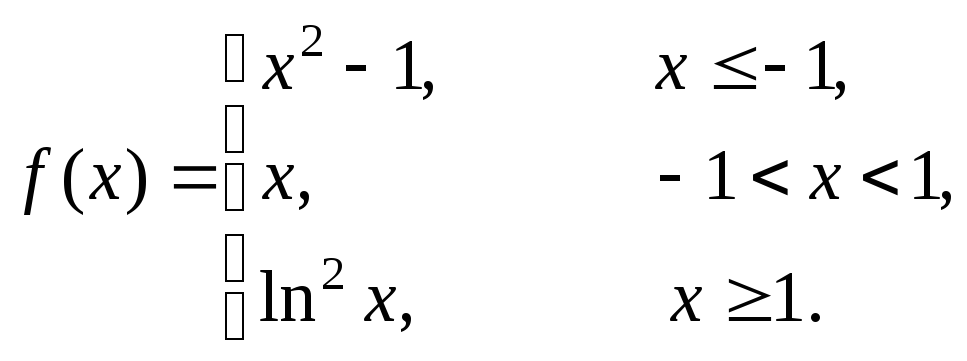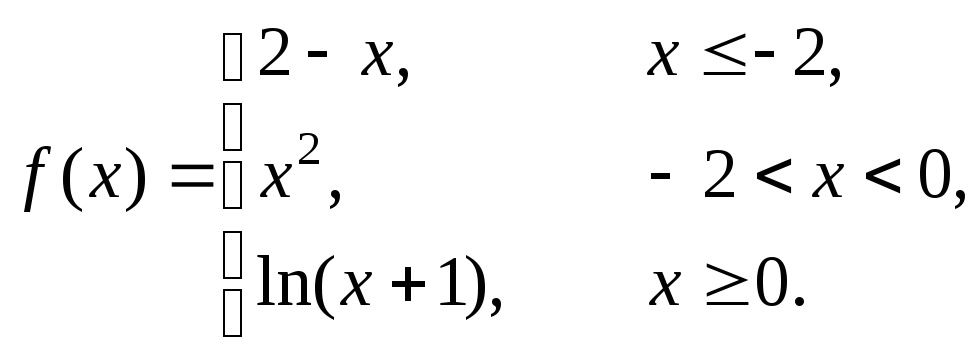- •Государственное общеобразовательное учреждение высшего профессионального образования
- •Подписано в печать11.02.2008. Формат .
- •Четность и нечетность функций
- •Периодичность функций
- •Задание 3. Найти наименьший период функции
- •Простейшие преобразования графиков
- •1.2. Непрерывность и точки разрыва функции
- •1.3. Асимптоты графика функции
- •1.4. Интервалы монотонности и точки экстремума функции
- •Нахождения наибольшего и наименьшего значения непрерывной функции на отрезке
- •1.5. Интервалы выпуклости и вогнутости, точки перегиба функции
- •1.6. Схема полного исследования функции и построение ее графика
- •2. Раскрытие неопределенностей
- •Содержание
- •1. Исследование функции 3
- •Задание 11. 36
- •2. Раскрытие неопределенностей. Правило Лопиталя 38
1.2. Непрерывность и точки разрыва функции
Функция
![]() называетсянепрерывной
в точке
называетсянепрерывной
в точке
![]() если:
если:
1)
![]() определена в точке
определена в точке![]() и её окрестности;
и её окрестности;
2)
существует конечный предел функции
![]() в точке
в точке![]() ;
;
3)
этот предел равен значению функции в
точке
![]() ,
т.е.
,
т.е.
![]()
Функция,
непрерывна в каждой точке некоторой
области, называется непрерывной
в этой области.
Точка
![]() ,
в которой нарушено хотя бы одно из трех
условий непрерывности функции, называетсяточкой разрыва
функции.
,
в которой нарушено хотя бы одно из трех
условий непрерывности функции, называетсяточкой разрыва
функции.
Точка
![]() называется точкой разрывапервого
рода, если
функция
называется точкой разрывапервого
рода, если
функция
![]() имеет в этой точке конечный правый и
левый предел, т.е.
имеет в этой точке конечный правый и
левый предел, т.е.
![]()
Если
хотя бы одна из этих пределов не
существует или равен бесконечности, то
точка
![]() называют точкой разрывавторого
рода.
называют точкой разрывавторого
рода.
Пример. Исследовать функцию
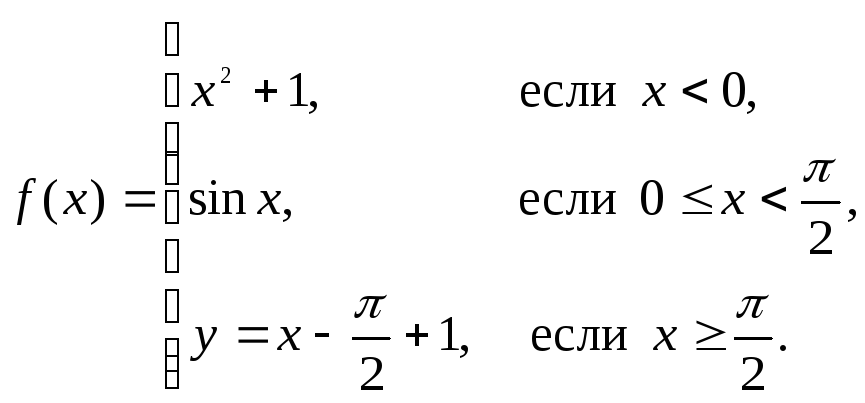
на непрерывность, построить её график.
Решение.
Функция
![]() определена и непрерывна на интервале
определена и непрерывна на интервале![]() т.к. на этих интервалах она задана
непрерывными элементарными функциями
т.к. на этих интервалах она задана
непрерывными элементарными функциями![]() .
Следовательно, разрыв возможен только
в точках
.
Следовательно, разрыв возможен только
в точках![]()
Для
точки
![]() имеем
имеем
![]() ,
,
![]() ,
,
![]() .
.
т.к.
![]() и оба они конечны, то функцияf(x)
в точке
и оба они конечны, то функцияf(x)
в точке
![]() имеет разрыв первого рода.
имеет разрыв первого рода.
Для
точки
![]() имеем
имеем
![]() ,
,
![]() ,
,
![]()
т.е.
![]() и в точке
и в точке![]() функция непрерывна.
функция непрерывна.
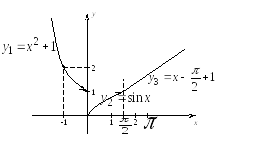
Пример.
Найдите точку разрыва функции
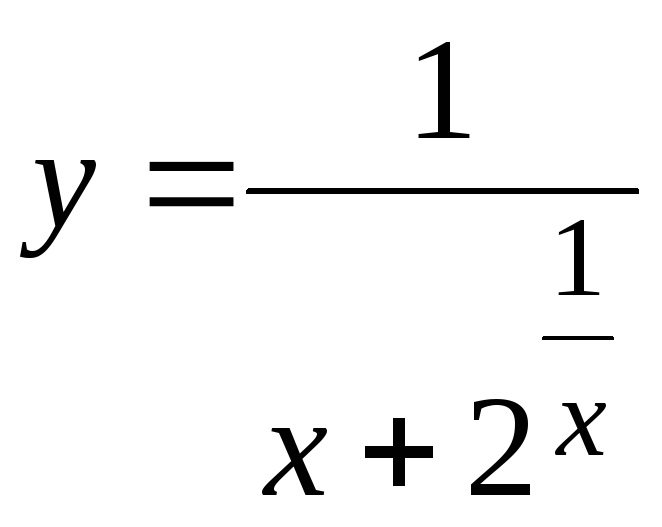 .
.
Решение.
Единственной точкой разрыва данной
функции является точка
![]() т.к. функция в этой точке не определена.
Найдем односторонние пределы в окрестности
точки
т.к. функция в этой точке не определена.
Найдем односторонние пределы в окрестности
точки![]() :
:
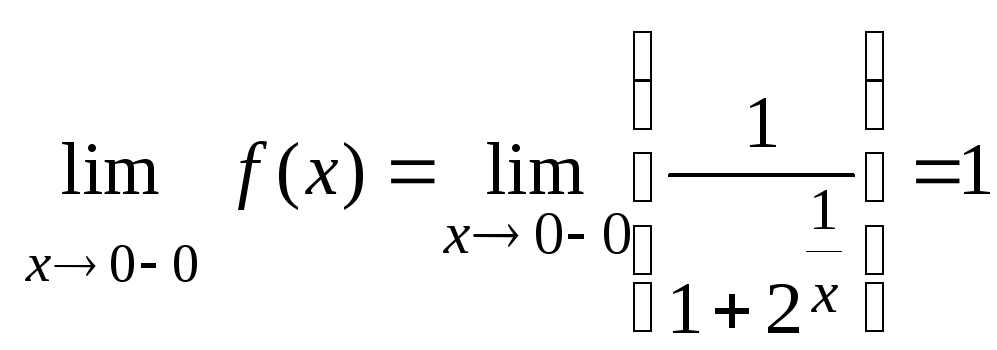 ,
т.к.
,
т.к.
![]() ,
,
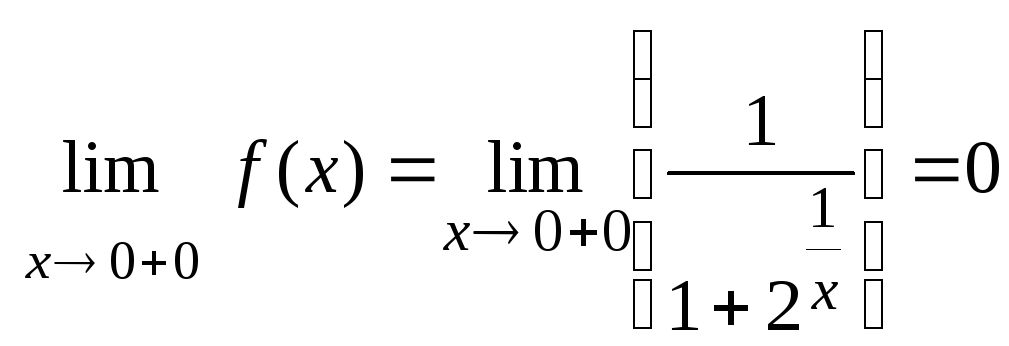 ,
т.к.
,
т.к.
![]() .
.
Т.к.
![]() то в точке
то в точке![]() имеем
разрыв первого рода.
имеем
разрыв первого рода.
Вычислим
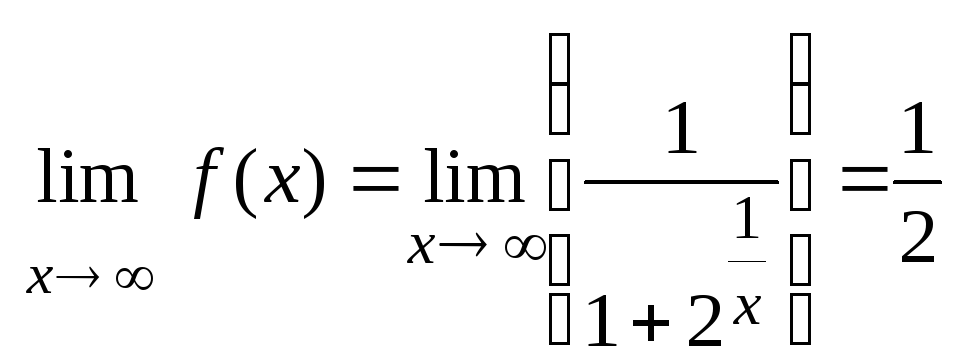 ,
т.к.
,
т.к.![]() ,
,
т.е.
![]() горизонтальная асимптота графика данной
функции.
горизонтальная асимптота графика данной
функции.

Задание 5.
Исследовать данные функции на непрерывность и построить их графики
|
№ зад. № вар. |
1 |
2 |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
1.3. Асимптоты графика функции
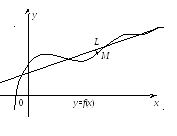
Прямая
L
называется асимптотой
данной кривой
![]() ,
если расстояние от точки М кривой до
прямойL
при удаление точки М в бесконечность
стремится к нулю.
,
если расстояние от точки М кривой до
прямойL
при удаление точки М в бесконечность
стремится к нулю.

Если
существует числа
![]()
![]() при которой
при которой![]() ,
т.е. функция имеет бесконечный разрыв,
то прямые
,
т.е. функция имеет бесконечный разрыв,
то прямые![]() называютсявертикальными
асимптотами кривой
называютсявертикальными
асимптотами кривой
![]() .
.
Если существуют пределы
![]() то
прямая
то
прямая
![]() являетсянаклонной
асимптотой кривой
являетсянаклонной
асимптотой кривой
![]() (приk=0
- горизонтальной).
(приk=0
- горизонтальной).
Пример.
Найти асимптоты графика функции
![]() .
.
Решение.
Функция терпит разрыв в точке
![]() .
Находим левый и правый пределы в этой
точке
.
Находим левый и правый пределы в этой
точке
![]() ,
,
![]() .
.
Таким
образом
![]() - вертикальная асимптота графика функции.
- вертикальная асимптота графика функции.
Находим
![]() ,
поэтому у=4
- горизонтальная асимптота.
,
поэтому у=4
- горизонтальная асимптота.

Пример.
Найти асимптоты графика функции
![]() .
.
Решение.
Данная функция терпит разрыв в точке
![]() .
Находим
.
Находим
![]() ,
,
![]() .
.
Поэтому
прямая
![]() является вертикальной асимптотой
графика функции.
является вертикальной асимптотой
графика функции.
Находим горизонтальные асимптоты.
![]() ,
,
![]() ,
,
следовательно,
прямая
![]() является наклонной асимптотой графика
данной функции.
является наклонной асимптотой графика
данной функции.

Задание 6.
Найти асимптоты графика функции
|
№ зад. № вар. |
1 |
2 |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|