MATHCAD
.pdfi |
di |
Si |
Ri |
0 |
0.5 |
–6 |
3 |
1 |
1 |
–5.7 |
2 |
2 |
1.5 |
–6.4 |
–1 |
3 |
2 |
–2 |
2.6 |
4 |
2.5 |
–1 |
3 |
Вариант 21
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.4 |
5 |
2.6 |
1 |
0.8 |
4 |
3.9 |
2 |
1.2 |
3 |
5 |
3 |
1.6 |
4 |
3.6 |
4 |
2 |
5.5 |
2.7 |
Вариант 22
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
0.8 |
3 |
1 |
1 |
0.5 |
2.1 |
2 |
1.5 |
0 |
0.1 |
3 |
2 |
0.4 |
0.3 |
4 |
2.5 |
0.9 |
4 |
Вариант 23
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
2.8 |
7.5 |
1 |
1 |
3.9 |
5 |
2 |
1.5 |
5.7 |
4 |
3 |
2 |
3.8 |
5.7 |
4 |
2.5 |
2.6 |
6 |
61
Вариант 24
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
2 |
7 |
1 |
1 |
7 |
2.2 |
2 |
1.5 |
4 |
5 |
3 |
2 |
8.8 |
3 |
4 |
2.5 |
3 |
10 |
Вариант 25
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
1.1 |
5 |
1 |
1 |
3 |
3.6 |
2 |
1.5 |
2.3 |
4.8 |
3 |
2 |
1.3 |
2 |
4 |
2.5 |
0 |
1 |
Вариант 26
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
3.5 |
7.1 |
1 |
1 |
6 |
4 |
2 |
1.5 |
9 |
0 |
3 |
2 |
6.8 |
4.6 |
4 |
2.5 |
5 |
6 |
Вариант 27
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
62
i |
di |
Si |
Ri |
0 |
0.2 |
–3 |
3 |
1 |
0.4 |
–4 |
5 |
2 |
0.6 |
–5 |
7.1 |
3 |
0.8 |
–4.1 |
6.4 |
4 |
1 |
–2.9 |
3.2 |
Вариант 28
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X–Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
4.3 |
7.9 |
1 |
1 |
5.6 |
6 |
2 |
1.5 |
7.9 |
3 |
3 |
2 |
5.7 |
4.7 |
4 |
2.5 |
2 |
7 |
Вариант 29
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
1.7 |
6 |
1 |
1 |
0 |
3 |
2 |
1.5 |
-3 |
0 |
3 |
2 |
–0.7 |
5 |
4 |
2.5 |
2 |
10.1 |
Вариант 30
Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Si(di) и Ri(di), используя команду Вставка/График/X-Y Зависимость. Провести форматирование полученных графиков.
i |
di |
Si |
Ri |
0 |
0.5 |
1.1 |
2.4 |
1 |
1 |
2.3 |
5.1 |
2 |
1.5 |
5.8 |
9 |
3 |
2 |
2.7 |
4.1 |
4 |
2.5 |
1.1 |
13 |
63
ЗАДАНИЕ 6. Работа с полярными графиками в MathCAD
Пример А.6 Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/30.
X : sin 
3 Y : 1 cos .
Решение
1. Присваиваем значения дискретному аргументу α. Для этого выполняем последовательно следующие действия:
вводим переменную α, используя панель инструментов
MATH→GREEK;
нажимаем кнопку 
на панели инструментов MATH→CALCULATOR;
вводим число 0 (начало диапазона);
вводим выражение π/30 для определения шага, используя панель
MATH→CALCULATOR;
нажимаем клавишу : в английской раскладке клавиатуры (для символа диапазона);
вводим выражение 2·π (конец диапазона);
ниже или левее вводим с клавиатуры переменную α и нажимаем
знак 
.
На экране отображается таблица значений для дискретного аргумента α.
2.Определяем функции X(α) и Y(α), используя панели инструментов
MATH→CALCULATOR и MATH→GREEK.
3.Далее строим полярные графики функций X(α) и Y(α).
заходим в меню ВСТАВКА→ГРАФИК→Polar Plot (Insert→Graph→ Polar Plot t);
в появившемся окне графической области заполняем маленькие темные прямоугольники: внизу графической области вводим α, слева от графической области – X(α), ставим запятую и вводим Y(α);
щелкаем правой кнопкой мыши в свободной части документа. В графической области отображаются графики функций X(α) и Y(α).
4.Проведем форматирование полученных графиков. Для этого выполним действия, аналогичные действия пункта 4 практической работы №5. Вид отредактированных графиков представлен на рисунке А6.
5.Сохраняем файл.
64
Рисунок А.6
ВАРИАНТЫ ЗАДАНИЙ
Вариант 1
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/30.
X : sin 4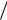 
3 Y : 1.5 1 cos .
Вариант 2
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/29.
X : tg 6 
3 Y : 8.5 1 sin .
Вариант 3
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/27.
X : ctg 0.6 
3 Y : 10.5 1 cos 4 .
65
Вариант 4
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/30.
X : sin 5 
6 Y : 1.5 1 cos 8
Вариант 5
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/21.
X : cos 7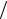 
6 Y : 3.5 1 cos 6
Вариант 6
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/30.
X : 2 2 cos 2 |
Y : 5 |
Вариант 7
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/22.
X : 4 cos3 8 |
Y : 1 cos 8 |
Вариант 8
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/30.
X : 4 cos3 4 |
Y : 1 sin 6 |
Вариант 9
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/29.
X : sin |
6 |
Y : |
4 |
|
2 cos 3 |
||||
|
|
|
Вариант 10
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/24.
X : sin 6 Y : 4 cos cos 2
Вариант 11
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/25.
X : tg 
7 Y : 1 cos 8
66
Вариант 12
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/30.
X : 7 2 cos 3 |
Y : 18 |
Вариант 13
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/20.
X : tg 4 
3 Y : 52 sin( ) cos(6 )
Вариант 14
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/21.
X : ctg 0.5 
3 Y : 22 sin cos 8
Вариант 15
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/22.
X : 4 cos 2 Y : sin2 2 cos2 42
Вариант 16
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/23.
X : 8 cos 2 cos 8 |
Y : sin2 2 cos2 42 |
Вариант 17
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/24.
X : cos |
6 |
Y : |
4 |
|
2 cos 6 |
||||
|
|
|
Вариант 18
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/25.
X : sin 5 
3 Y : sin2 cos2 12
Вариант 19
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/26.
X : sin |
Y : |
4 |
|
4 cos 6 |
|||
|
|
67
Вариант 20
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/27.
X : sin 7 
6 Y : 0.8 cos 3 sin2
Вариант 21
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/28.
X : cos 
8 Y : 
8 cos 2
Вариант 22
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/29.
X : sin 5 
2 Y : 1.6 cos 3 sin2
Вариант 23
Построить графики функций X(α) и Y(α) в полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/30.
X : cos 
4 Y : 8 cos 5 sin2
Вариант 24
Построить графики функций в X(α) и Y(α) полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/20.
X : sin 5 |
3 |
Y : 2 sin 8 |
Вариант 25
Построить графики функций в X(α) и Y(α) полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/28.
X : cos 5 |
6 |
Y : |
8 |
|
2 sin 9 |
||||
|
|
|
Вариант 26
Построить графики функций в X(α) и Y(α) полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/24.
|
5 |
8 |
|
||
X : cos |
|
|
Y : |
|
|
|
2 sin 3 |
||||
|
8 |
|
|||
Вариант 27
Построить графики функций в X(α) и Y(α) полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/29.
X : cos 
4 Y : 
0.08 cos 4
68
Вариант 28
Построить графики функций в X(α) и Y(α) полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/15.
X : sin 3 Y : 2 sin2 8
Вариант 29
Построить графики функций в X(α) и Y(α) полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/25.
X : cos 5 
4 Y : 
0.32 cos 6
Вариант 30
Построить графики функций в X(α) и Y(α) полярной системе координат через аргумент, заданный дискретно: α изменяется от 0 до 2π с шагом π/20.
X : |
4 |
Y : sin 4 |
2 cos 3 |
69
ЗАДАНИЕ 7 Построение поверхностей в MathCAD
Пример А.7
1. Создать поверхности для функций двух переменных с использованием функции CreateMesh:
X t, : t sin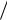 
4 Y t, : t 1 cos2 ,
где t изменяется от –4 до +4, α – от 0 до 2·π, сетка размером 50х50.
2. Отобразить графически пересечение выше описанных поверхностей. Выполнить однотонную заливку для поверхностей.
Решение
1.Присваиваем значения функциям X(t,α) и Y(t,α) с использованием панелей инструментов MATH→CALCULATOR и MATH→GREEK.
2.Определяем поверхности, определяемые функциями X(α) и Y(α), используя функцию CreateMesh. Для функции X(α) выражение имеет вид:
M:=CreateMesh(X,-4,4,0,2·π,50,50); для функции Y(α) выражение имеет вид: M1:=CreateMesh(Y,-4,4,0,2·π,50,50) (см. рисунок А.7).
3.Далее строим поверхности М и М1. Для этого выполняем следующие действия:
заходим в меню ВСТАВКА→ГРАФИК→Surface Plot (Insert→Graph→ Surface Plot t);
в появившемся окне графической области заполняем маленький темный прямоугольник: вводим М, ставим запятую, вводим М1;
щелкаем правой кнопкой мыши в свободной части документа. В графической области отображаются поверхности функций двух переменных М
иМ1.
4. Проведем форматирование полученных графиков. Для этого вызовем контекстное меню графика поверхностей. Вид отредактированных графиков представлен на рисунке А.7.
70