Глава 3 электрические цепи переменного синусоидального тока
3.1 Получение синусоидальной э.Д.С (Рис.3.1).
Электрический ток называется переменным, если он периодически меняет величину и направление, то есть следует периодическому закону изменения. Синусоидальный ток - это ток периодический, величина которого меняется по синусоидальному закону во времени.
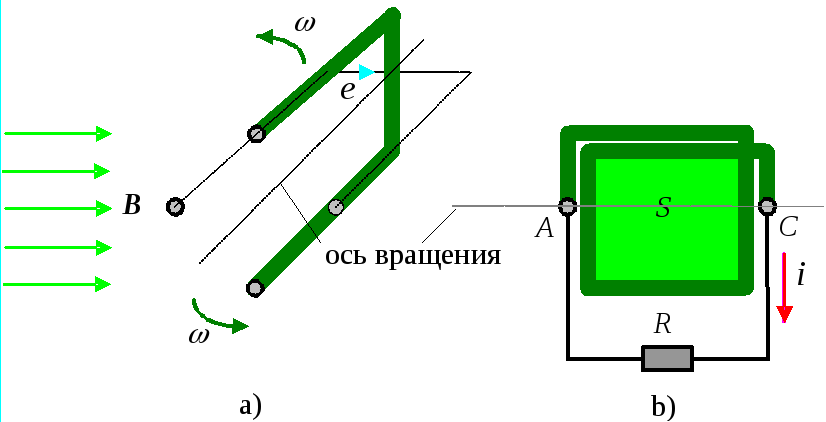
Рис.3.1
Заставим вращаться вокруг воображаемой оси виток проводника с постоянной, угловой частотой в магнитном поле с индукцией B.
Согласно закону Ленца э.д.с. на зажимах АС будет
.
Подставляя
,
получим
, (3.1)
где: B - магнитная индукция [Tл],
S
- площать витка [
],
- угловая частота (пульсация) [рад/сек].
Если присоединить к зажимам АС резистор R, то по цепи потечет синусоидальный ток
, (3.2)
где
.
3.2 Графическое представление синусоидальных величин (Рис.3.2)
Рис.3.2
Рисунок 3.2 показывает:
i - мгновенное значение тока [A],
-
максимальное
значение тока (амплитуда) [A],
T - период [сек],
- пульсацию [рад/сек], = 2f, где f = 1/T [Гц],
- начальная фаза [град] или [рад].
Угол определяет разность фаз, например:
;
.
Когда = 0, эти две величины находятся в фазе.
Когда = /2, эти две величины находятся в квадратуре.
Когда =, эти две величины находятся в противофазе.
Действующее (эффективное) значение тока I может быть определено по формуле:
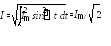
(3.3)
Замечание:
Все рассмотренные величины и значения справедливы, как для тока, так и для напряжения и электродвижущей силы.
3.3 Векторное представление синусоидальных величин (Рис.3.3)
Если
несколько величин
имеют
одинаковую пульсацию
ω
и отличаются только амплитудой
и начальной
фазой ψ,
то возможно упростить их представление.
Например, величины
;
; (3.4)
;
будут
представлены на Рис.3.3, для времени
t
= 0 в
виде векторов
,
и
,
которые вращаются с угловой скоростью
вокруг оси
O.
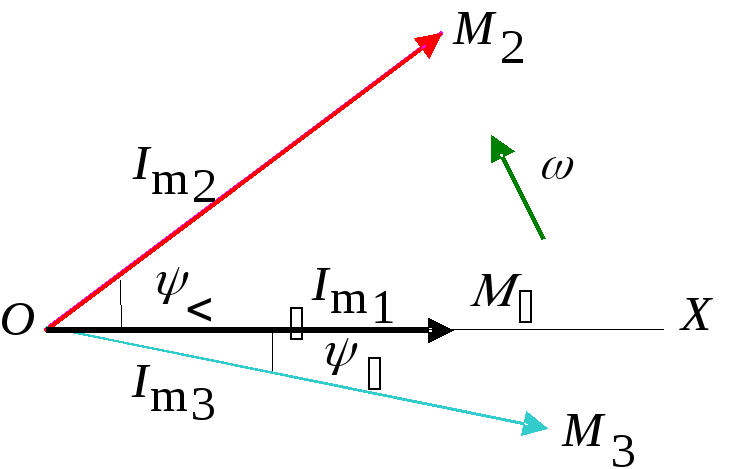
Рис.3.3
На этой фигуре, имеем:
OX - ось координат;
,
и
-
модули векторов, которые могут быть
равны
максимальным
,
и
или
действующим
,
и
значениям токов;
,
и
-
начальные
фазы
токов
,
и
.
3.4 Представление синусоидальных величин с помощью комплексных чисел (Рис.3.4)
Сведения из курса математики.
откуда
- мнимая
единица.
-комплексное
число в
алгебраической
форме.
где: a - реальная часть комплексного числа,
b - мнимая часть комплексного числа.
Графическое представление в комплексных координатах изображено на Рис.3.4.
Вектор
представляет
комплексное число
.
Из
этого рисунка следует, что
-
модуль
комплексного числа, а
= arctg b/a - аргумент этого числа.
Поэтому в тригонометрической форме комплексного числа получим:
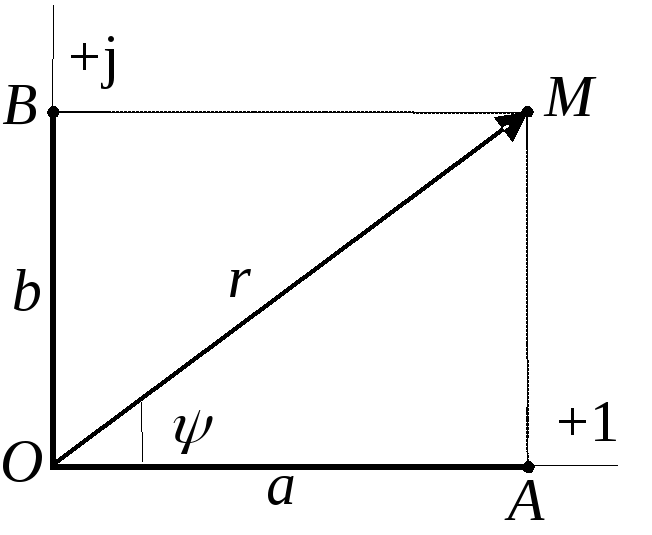
Рис.3.4
Согласно
соотношению Ейлера, имеем
,
где 
.
Таким образом, получаем экспоненциальную (полярную) форму комплексного числа.
Любая
синусоидальная
величина
представленная в виде вектора, например
,
может быть ассоциирована с комплексным
числом
,
модуль которого
I
действующее
значение тока и
аргумент
начальная
фаза.
То есть три синусоидальных тока (Рис.3.2) могут быть представлены в виде комплексных чисел:
;
; (3.5)
.
Рисунок 3.5 показывает эти три тока на комплексной плоскости.
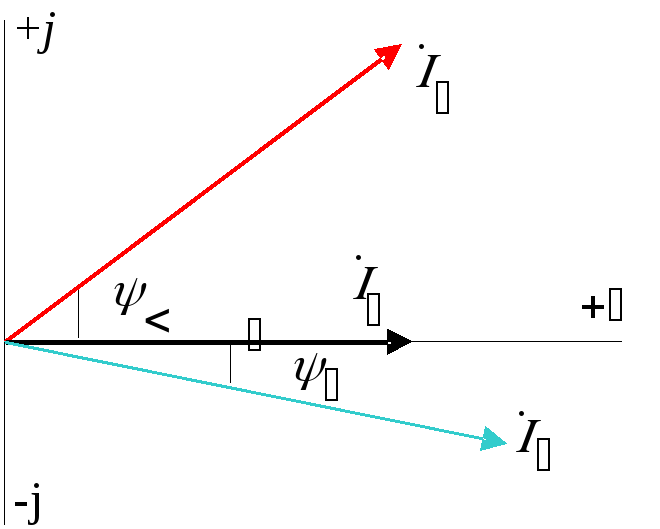
Рис.3.5