14 Лекция №13. Минимизация логических функций

Продолжительность:2 часа (90 мин.)

14.1 Ключевые вопросы

14 Лекция №13. Минимизация логических функций 1

14.1 Ключевые вопросы 1

14.2 Текст лекции 1

14.2.1 Минимизация логических функций 1

14.2.1.1 Расчетный метод 1

14.2.1.2 Карты Карно 4

14.2.2 Минимизация систем логических уравнений 7

14.2.3 Минимизация частично определенных логических функций 8

14.2.4 Вопросы для контроля 10

14.2 Текст лекции

14.2.1 Минимизация логических функций

Существует достаточно много методов минимизации логических функций, приведем только два метода, которые чаще всего применяются в инженерной практике:

• расчетный;

• карт Карно.

14.2.1.1 Расчетный метод

Здесь применяют:

– склеивание,

– поглощение,

– развертывание.

Склеивание

а) Если в выражении встречается сумма двух конъюнкций, в одной из которых одна из переменных стоит в прямом значении, а в другой в инверсном значении, а остальные переменные одинаковые, то эту сумму конъюнкций, можно заменить одной конъюнкцией, не содержащей переменную, имеющую разные значения:

Конъюнкции, отличающиеся только значениями одной переменной (в одну из них переменная входит без отрицания, а в другую с отрицанием), называются соседними.

Замечание:Это правило основано на законе дополнительностии дистрибутивном законе конъюнкции относительно дизъюнкции (см. Лекцию № 10)

.

б) Если в выражении встречается произведение двух дизъюнкций, в одной из которых одна из переменных стоит в прямом значении, а в другой в инверсном значении, а остальные переменные одинаковые, то это произведение дизъюнкций, можно заменить одной дизъюнкцией, не содержащей переменную, имеющую разные значения:

.

Дизъюнкции, отличающиеся только значениями одной переменной (в одну из них переменная входит без отрицания, а в другую с отрицанием), называются соседними.

Замечание:Это правило основано на законе дополнительности

и дистрибутивном законе дизъюнкции относительно конъюнкции (см. Лекцию № 10)

.

в) Правила обобщенного склеивания.

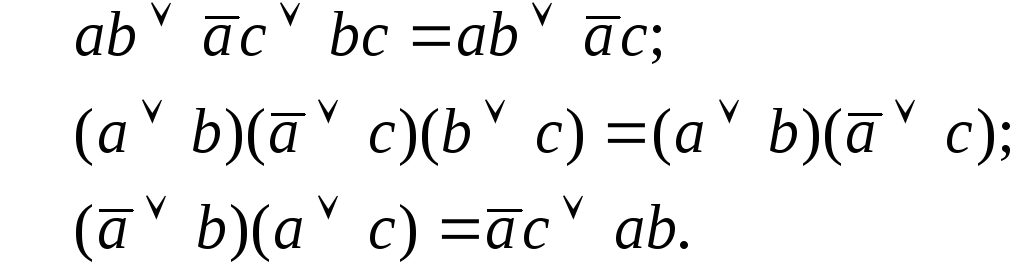
В первом случае исчезло произведение bc, во втором исчезает суммаbc, в третьем снова произведениеbc(третий случай после раскрытия скобок сводится к первому). Доказываются эти правила, как обычно, составлением и сравнением таблиц истинности для левой и правой части или с помощью развертывания (см. ниже).

Поглощение

а) Если в выражении встречается сумма двух произведений, одно из которых является частью другого, то эту сумму можно заменить меньшим произведением:

.

б) Если в выражении встречается произведение двух сумм, одна из которых является частью другой, то это произведение сумм можно заменить меньшей суммой:

a(ab) = a; a(ab)(ac)…= a; (ab)(abc)= ab.

Развертывание

Развертывание позволяет восстановить в формулах «потерянные» (например, в результате минимизации) переменные или перейти от ДНФ и КНФ к совершенным формам – СДНФ и СКНФ. Восстановление переменных для ДНФ и КНФ производится по–разному. Рассмотрим примеры.

Пусть имеем ДНФ

xz,

в которой, очевидно, потеряна переменная y. Для восстановления переменнойyпроизведение переменныхxzумножается на 1, затем 1 заменяется суммой прямого и инверсного обозначений недостающей переменной, и на основе дистрибутивного закона проводится преобразование

.

Пусть имеем КНФ , где также потеряна переменнаяy. Для ее восстановления к суммедобавляется 0, затем 0 заменяется произведением недостающей переменной на ее инверсию и применяется дистрибутивный закон

Используя развертывание, можно раскрыть смысл понятий «конституента единицы» и «конституента нуля».

Пусть n= 2 (переменныеaиb).

Развернем единицу 1.

1= 1==.

Получили СДНФ функции двух переменных f= 1, где каждая конъюнкция является составляющей (конституентой) единицы.

Развернем 0.

0 =

Получили СКНФ функции двух переменных f= 0, где каждая дизъюнкция является составляющей (конституентой) нуля.

Полезность развертывания показывает пример доказательства правил обобщенного склеивания (см. п. 4.1.1):

Рассмотрим первое правило

Развернем левую часть тождества, в первом произведении которой недостает переменной c, во втором произведении недостаетb, а в третьем нетa.

После приведения подобных членов, применив простое склеивание

получаем правую часть, следовательно, тождество доказано.

Рассмотрим второе правило

.

Развернем левую часть тождества.

Используя дистрибутивный закон дизъюнкции относительно конъюнкции, получаем

После приведения подобных членов, применив простое склеивание, будем иметь

Получили правую часть, следовательно, правило доказано.

Общий порядок проведения минимизации функции, заданной СДНФ, здесь следующий.

1. Сначала к членам СДНФ применяется операция склеивания (каждая конъюнкция может использоваться многократно, объединяясь с разными членами). При этом из них исключается по одной переменной. Затем приводятся подобные члены, и снова проводится склеивание. Этот процесс продолжается, пока в получаемом выражении не останется конъюнкций, отличающихся друг от друга значениями одной переменной. Полученное выражение называетсясокращенной нормальной формой. Каждой логической функции соответствует лишь одна такая форма.

2. К сокращенной нормальной форме применяется операция обобщенного склеивания. В результате из нее исключаются лишние конъюнкции. Процесс продолжается, пока склеивания становятся невозможными. Получаемая форма называется тупиковой формойлогической функции. Тупиковых форм у логической функции может быть несколько.

3. Полученная тупиковая форма случайно может оказаться минимальной. В общем случае для поиска минимальной формы необходим перебор тупиковых форм.

С функциями, представленными в СКНФ, поступают аналогично с учетом их особенностей. Иногда оказывается удобно на промежуточном этапе перейти к дизъюнктивной нормальной форме и продолжать минимизацию так, как изложено выше.

Пример 1:Минимизировать функцию

После применения операции склеивания и приведения подобных членов получаем

Обобщенное склеивание здесь можно проводить по нескольким вариантам, которые дают следующие результаты:

.

Исключены ,,: (), (), ().

В скобках показаны термы, участвующие в обобщенном склеивании.

Исключены ,,: (), (), ().

Как видим, здесь имеется две минимальных нормальных формы. По сложности они одинаковы.

Пример 2:Продолжая решение задачи по созданию устройства рис. 3, проведем минимизацию мажоритарной функции (см. табл. 12), для которой выше были получены СДНФ и СКНФ.

СДНФ:

.

СKНФ:

Здесь первую сумму мы поочередно рассматривали в паре со второй, третьей и четвертой суммами и после склеивания этих пар получили результат.