12 Лекция №11. Формы задания логических функций

Продолжительность:2 часа (90 мин.)

12.1 Ключевые вопросы

12 Лекция №11. Формы задания логических функций 1

12.1 Ключевые вопросы 1

12.2 Текст лекции 1

12.2.1 Формы задания логических функций 1

12.2.1.1 Словесная форма 1

12.2.1.2 Табличная форма 1

12.2.1.3 Задание формулой 2

а) Совершенная дизъюнктивная нормальная форма 2

б) Совершенная конъюнктивная нормальная форма 3

в) Дизъюнктивные и конъюнктивные нормальные формы 6

г) Минтермы, макстермы и их свойства 6

12.2.1.4 Другие формы задания логических функций 7

12.2.1.5 Вопросы для контроля 11

12.2 Текст лекции

12.2.1 Формы задания логических функций

Наиболее часто употребляются следующие формы задания логических функций:

• Словесная;

• Табличная;

• Аналитическая;

• Схемная.

12.2.1.1 Словесная форма

Словесная форма дается в виде задания на проектирование некоторого устройства.

Пример:Создать устройство рис. 12.1, которое будет выдавать на выходеy сигнал, значения которого определяются по большинству значений входных сигналовa,b,c.

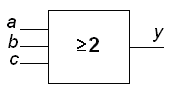
Рисунок 12.1 – Условное обозначение мажоритарного элемента

Такие устройства содержат нечетное число входов 3 и называются элементами голосования или мажоритарными элементами, так как реализуют они мажоритарную функцию, обозначаемую иногда

y = a # b # c.

12.2.1.2 Табличная форма

Логические функции можно представить в виде двух типов таблиц:

– Таблиц истинности;

– Карт Карно (см. Лекцию № 13).

Порядок получения таблицы истинностилогической функции таков.

Сначала составляется заготовка таблицы, в которой размещаются все возможные наборы nпеременных (входные наборы) с учетом их веса (номера), затем в нее проставляются значения логической функции по ее словесному описанию.

В рассматриваемом случае значение функции yбудет 0, если большинство входных переменных имеют значение 0. Значение функции будет 1, если на входах больше 1. В результате получаем табл. 12.1.

Таблица 12.1
№	с	b	a	y
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

12.2.1.3 Задание формулой а) Совершенная дизъюнктивная нормальная форма

Введем обозначения: если во входном набореа= 1, то будем писать «а», если в набореа= 0, то пишем «». Для других переменных аналогично.

Рассмотрим строки табл. 12.1, в которых функция y= 1.

Строка №3: y= 1, еслиa= 1,иb= 1,иc= 0.

Используя введенные обозначения переменных и заменив союз И символом конъюнкции, это условие для строки №3 можно записать так:

y= 1, если входной набор равен baили просто ba.

В строке №5 y= 1 при входном наборе ca.

В строке №6 y= 1 при входном набореcb.

В строке №7 y= 1 при входном набореcba.

Итак, y= 1 при наборе ba,илипри набореca,илипри набореcb,илипри набореcba, что можно записать, заменив союз ИЛИ символом дизъюнкции, так

y = bacacbcba = 1.

Единицу обычно не пишут (но всегда подразумевают), поэтому окончательно получаем:

y = bacacbcba .

Каждый член этой суммы (дизъюнкции) есть произведение (конъюнкция) всех аргументов или их отрицаний и носит название минтерма или конституентыединицы, а полученная сумма называетсясовершенной дизъюнктивной нормальной формой (СДНФ) логической функции.

СДНФ для каждой логической функции единственна.

Понятия «минтерм» и «конституента единицы» будут пояснены ниже.

Полученная форма называется

• совершенной, так как все конъюнкции содержат все переменные (с отрицанием или без отрицания), т.е. имеют максимальный ранг;

• дизъюнктивной, потому что формула представляет собой дизъюнкцию конъюнкций;

• нормальной, так как все конъюнкции являются элементарными.

Если в конъюнкцию входят только переменные или их отрицания, то конъюнкция называется элементарной. Число переменных в конъюнкции называется еерангом. В нашем случае ранг конъюнкций равен 3.