13)----Интерференционный опыт Юнга. Ширина интерференционной полосы.

Исторически первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S₁ и S₂ (рис. 6.7.3). Проходя через каждую из щелей, световой пучок расширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щелиS₁ и S₂, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

В опыте щели S₁ и S₂ освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S₁ и S₂, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r₁ и r₂. Следовательно, фазы колебаний, создаваемых волнами от источников S₁ и S₂ в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S₁ и S₂ распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.

Ширина интерференционных полос — это расстояние на экране между двумя соседними светлыми или двумя темными полосами.

15)---Ко́льца Нью́тона — кольцеобразные интерференционныемаксимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклойлинзыи плоскопараллельной пластины при прохождениисветасквозьлинзуи пластину .Простая интерференционная картина возникает в тонкой прослойкевоздухамежду стеклянной пластиной и положенной на нее плосковыпуклойлинзой, сферическая поверхность которой имеет большойрадиускривизны. Этаинтерференционнаякартина имеет вид концентрическихколец, получивших названиекольца Ньютона.

Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизнылинзы) в отражённом свете выражается следующей формулой:

где

R — радиус кривизны линзы;

k = 0, 1, 2, …;

λ — длина волнысвета ввакууме;

n — показатель преломлениясреды между линзой и пластинкой.

16)---Дифракция света

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д. Например, звук хорошо слышен за углом дома, т. е. звуковая волна его огибает. Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн: Каждый участок фронта волны является источником вторичных сферических волн.

Зоны Френеля - участки, на которые можно разбить поверхность световой (или звуковой) волны для вычисления результатов дифракции света (или звука).

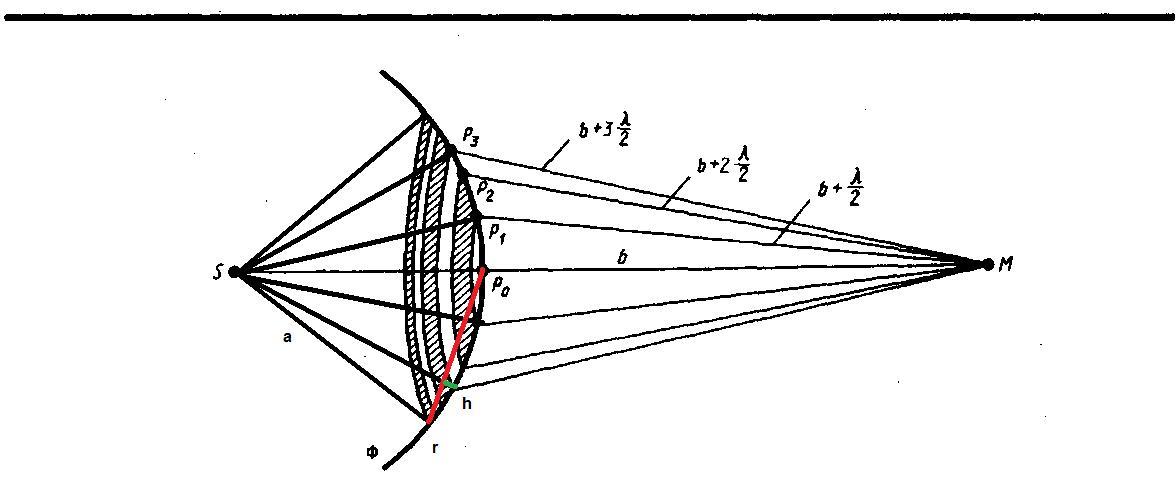
17)Метод зон Френеля:Принцип Гюйгенса — Френеля в рамках волновой теории должен был ответить на вопрос о прямолинейном распространении света. Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на /2Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на /2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М

где А₁, А₂, ... — амплитуды колебаний, возбуждаемых 1-й, 2-й, ..., т-й зонами

Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точ­ке М сферы радиусами b + ,b + 2,b + 3, ... .а-расстояние от источника до волнового фронта, в-расстояние от центра волнового фронта до точкинаблюдения, r-радиус внешней границы

Из рисунка следует, что

(177.2)

После элементарных преобразований, учитывая, что <<a и <<b, получим

Площадь сферического сегмента и площадь т-й зоны Френеля соответственно равны

Выражение (177.4) не зависит от т, следовательно, при не слишком больших т площа­ди зон Френеля одинаковы. Таким образом, построение зон Френеля разбивает волно­вую поверхность сферической волны на равные зоны.

Согласно предположению Френеля, действие отдельных зон в точке М тем меньше, чем больше угол _т ,т. е. действие зон постепенно убывает от центральной (около Р₀) к периферичес­ким.

амплитуда колебания А_m от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т. е.

Тогда выражение (177.1) можно записать в виде

амплитуда результирующих колебаний в произвольной точке М определяется как бы действием только половины центральной зоны Френеля.

радиус внешней границы т-й зоны Френеля: