15. Задача:

Идеальный газ имеет минимальную внутреннюю энергию в состоянии …

Решение:

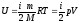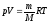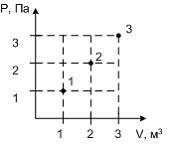
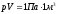Внутренняя энергия идеального газа равна (учитываем, что), гдеp - давление, V - объем, i - полное число степеней свободы, R - универсальная газовая постоянная, T - абсолютная температура, m - масса газа, M - молярная масса газа. В нашем случае минимальное значение произведения соответствует состоянию газа, обозначенному на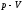- диаграмме точкой 1. Следовательно, идеальный газ имеет минимальную внутреннюю энергию в состоянии 1.

16. Задача:

На рисунке изображен цикл Карно в координатах (T, S), где S – энтропия. Адиабатное расширение происходит на этапе …

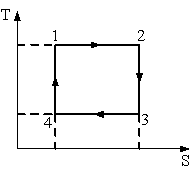
Решение:

Адиабатные процессы происходят без теплообмена с окружающей средой, т.е. система не получает тепла и не отдает его, 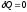. Так как изменение энтропии определяется как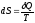, следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном расширении газ совершает работу за счет уменьшения внутренней энергии: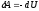, температура газа уменьшается. Адиабатное расширение происходит на этапе 2 – 3.

17. Задача

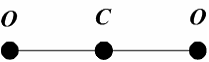
Если не учитывать колебательные движения в линейной молекуле углекислого газа (см. рис.), то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно …

Решение

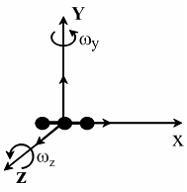
Средняя кинетическая энергия молекулы равна , где– постоянная Больцмана,– термодинамическая температура,– сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:. Для линейной молекулы углекислого газа(см. рис.) число степеней свободы поступательного движения, вращательного –, колебательного –, поэтому.Следовательно, средняя кинетическая энергия молекулыравна. Средняя энергия вращательного движенияи составляет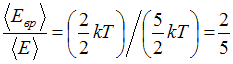части от полной энергии.

18. Задача

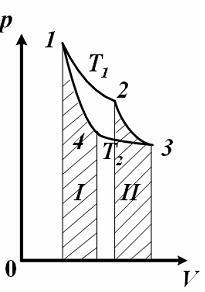На диаграмме изображен цикл Карно для идеального газа.Для величины работы адиабатического расширения газаи адиабатического сжатиясправедливо соотношение …

Варианты ответов:

работы невозможно сравнить

Решение:

Цикл Карно состоит из двух изотерм (изотермического расширения при температуреи изотермического сжатияпри температуре) и двух адиабат (адиабатического расширенияи адиабатического сжатия). При адиабатическом расширениии адиабатическом сжатиитеплообмен с окружающей средой отсутствует, и поэтому работы расширенияи сжатиясовершаются за счет изменения внутренней энергиии. Следовательно, работы газа в адиабатических процессахиравны по величине:, а  на-диаграмме графически определяются площадямиизаштрихованных фигур под графиками соответствующих процессов, и эти площади равны.

19. Задача

При увеличении давления в 3 раза и уменьшении объема в 2 раза внутренняя энергия идеального газа …

Решение:

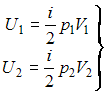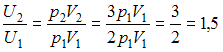Внутренняя энергия идеального газа равна (учитываем, что),  гдедавление,объем,полное число степеней свободы,универсальная газовая постоянная,абсолютная температура,масса газа,молярная масса газа.Учитывая,что , , получаем. Следовательно,.

Ответ: увеличится в 1,5 раза