
Экзаменационные задачи по механике и термодинамике
1. Задача:
Прямолинейное
движение точки описывается уравнением
 (в единицах СИ). Средняя скорость точки
за время движения до остановки в
(в единицах СИ). Средняя скорость точки
за время движения до остановки в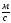 равна …
равна …
Решение:
Найдем
скорость:
 .
Приt=1c,
v=0.
Следовательно, время движения до
остановки равно 1c.
Средняя скорость за время движения до
остановки
.
Приt=1c,
v=0.
Следовательно, время движения до
остановки равно 1c.
Средняя скорость за время движения до
остановки
 .
.
Ответ:
 .
.
2. Задача:
 На
графике показано изменение с течением
времени ускорения точки на прямолинейном
отрезке пути. Начальная скорость равна
нулю. Скорость точки в момент времени
t2
равна …
На
графике показано изменение с течением
времени ускорения точки на прямолинейном
отрезке пути. Начальная скорость равна
нулю. Скорость точки в момент времени
t2
равна …
Решение:
Площадь,
ограниченная графиком, представляет
собой приращение скорости. За время
движения t1
приращение
скорости положительно и равно
 .
За время
.
За время приращение скорости отрицательно и
равно
приращение скорости отрицательно и
равно .
Поскольку начальная скорость равна
нулю, то скорость в момент времениt2
равна
.
Поскольку начальная скорость равна
нулю, то скорость в момент времениt2
равна
 .
.
Ответ:
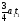
3. Задача
Тело движется вдоль оси x под действием силы, зависимость которой от координаты x представлена на рисунке:

Работа силы на пути l = l1 + l2 + l3 определяется выражением …
Решение:
Работа
переменной силы в случае одномерного
движения на участке
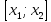 определяется как интеграл:
определяется как интеграл: .
На графике зависимости силы от координаты
искомая работа представлена площадью,
ограниченной кривой зависимости и осью
координат (геометрический смысл
интеграла). Следовательно, искомая
работа численно равна площади трапеции
ABCD, то есть произведению полусуммы
оснований на высоту:
.
На графике зависимости силы от координаты
искомая работа представлена площадью,
ограниченной кривой зависимости и осью
координат (геометрический смысл
интеграла). Следовательно, искомая
работа численно равна площади трапеции
ABCD, то есть произведению полусуммы
оснований на высоту: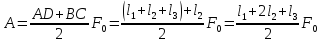 .
.

Ответ:
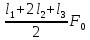
4. Задача
На
борту космического корабля, летящего
со скоростью 0,8 с относительно
неподвижной системы отсчета, произошли
два события, разделенные промежутком
времени ![]() .
В неподвижной системе отсчета длительность
этого промежутка равна …
.
В неподвижной системе отсчета длительность
этого промежутка равна …
Решение:
Из
преобразований Лоренца следует, что на
борту космического корабля, движущегося
относительно инерциальной системы
отсчета со скоростью, сравнимой со
скоростью света, наблюдается эффект
замедления хода времени. В неподвижной
системе отсчета длительность этого
промежутка равна  ,
где
,
где![]() –
скорость движения корабля,
–
скорость движения корабля,![]() –
скорость света.
–
скорость света.
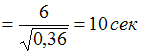 .
.
5. Задача:

За первые 3 секунды импульс тела изменится на …
Решение:
Согласно
второму закону Ньютона,
 .
В проекции на ось координат
.
В проекции на ось координат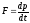 .
Следовательно,
.
Следовательно,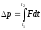 .
По геометрическому смыслу определенного
интеграла он равен площади под графиком
функции. Площадь под графиком функции
в интервале времени от 0 до 3 с равна 80
Нс,
следовательно, импульс тела изменится
на
.
По геометрическому смыслу определенного
интеграла он равен площади под графиком
функции. Площадь под графиком функции
в интервале времени от 0 до 3 с равна 80
Нс,
следовательно, импульс тела изменится
на
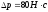 .
.
Ответ: 80 Нс
6. Задача:
Тонкостенная
трубка и кольцо, имеющие одинаковые
массы и радиусы, вращаются с одинаковой
угловой скоростью. Отношение величины
момента импульса трубки к величине
момента импульса кольца равно …

Решение:
Величина
момента импульса тела, вращающегося
вокруг неподвижной оси, определяется
по формуле
 ,
гдеJ
– момент инерции тела относительно
заданной оси,
- угловая скорость. Момент инерции
тонкостенной трубки равен
,
гдеJ
– момент инерции тела относительно
заданной оси,
- угловая скорость. Момент инерции
тонкостенной трубки равен
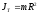 ;
момент инерции кольца, имеющего такую
же массу и радиус, равен моменту инерции
трубки, то есть
;
момент инерции кольца, имеющего такую
же массу и радиус, равен моменту инерции
трубки, то есть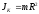 .
Отношение величин моментов импульсов
трубки и кольца равно:
.
Отношение величин моментов импульсов
трубки и кольца равно: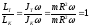 .
.
