Итак, треугольник cfd на плане скоростей подо-

бен треугольнику CFD группы на схеме и повернут относительно него на 90˚. Это свойство подобия фигуры относительных скоростей на плане скоростей фигуре звена на схеме механизма позволяет определить скорости любых точек этого звена не из уравнений (аналитически), а графически, построением подобных фигур.

Проверкой правильности графического построения подобных фигур на плане является совпадение порядка букв на схеме и на плане скоростей.

Планы скоростей обладают следующими свой-

ствами:

1.Векторы, выходящие из полюса, представляют собой абсолютные скорости.

2.Векторы, соединяющие концы абсолютных скоростей, являются относительными скоростями.

3.Векторы скоростей неподвижных точек обращаются в точки, располагающиеся в полюсе.

4.При построении плана скоростей применима теорема подобия.

3.7.Определение ускорений группы Ассура второго класса первого вида

При определении ускорений предполагают, что уже построен план скоростей группы и, следовательно, известны скорости всех звеньев группы. Также известны векторы абсолютных ускорений точек B и D концевых элементов группы, которыми звенья 2 и 3 входят во враща-

30

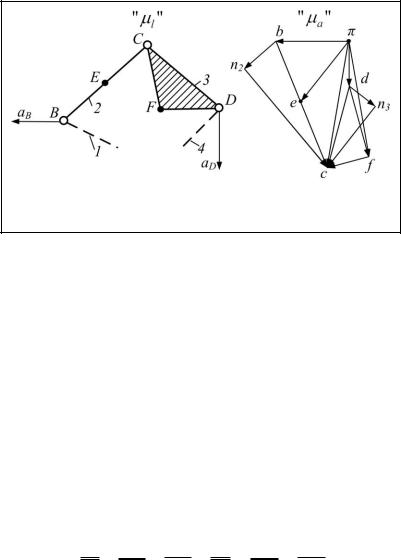
тельные кинематические пары с ведущими звеньями 1 и 4

(рис. 13).

Рис. 13. Определение ускорений группы Ассура второго класса первого вида

Принцип построения планов ускорений по существу мало чем отличается от построения планов скоростей. Прежними остаются последовательность в определении ускорений различных точек механизма и разложение сложного движения на его составляющие: поступательное и вращательное движения.

где aCBn и aCDn – нормальные ускорения в относительном вращательном движении;

aCBt и aCDt – тангенциальные ускорения в относительном вращательном движении.

Решая совместно уравнения, имеем:

aB aCBn aCBt aD aCDn aCDt .

31

Векторы нормальных ускорений могут быть определены как

Неизвестными являются величины векторов aCBt и

aCDt , которые могут быть определены построением плана

ускорений.

Выбираем в качестве полюса плана ускорений точку и откладываем ( b) и ( d ) , представляющие в

масштабе a ускорения точек B и D . Далее вычисляем величины ускорений aCBn и aCDn и откладываем из точек b

иd отрезки (bn2 ) и (dn3 ) , представляющие в масштабе

a эти ускорения. Из полученных точек n2 и n3 прово-

дим прямые в направлении векторов тангенциальных уско-

рений aCBt и aCDt .

Точка пересечения данных прямых и дает конец вектора aC абсолютного ускорения точки C .

aC a ( c) .

Соединив точки b и d плана с точкой c , получим векторы полных относительных ускорений aCB и aCD .

aCB a (cb) , aCD a (cd )

Пользуясь планом ускорений, можно определить угловое ускорение звеньев 2 и 3.

32

быть определены следующим образом. Перенося мысленно векторы aCBt и aCDt в точку C , видим, что направление2 совпадает с направлением вращения часовой стрелки, а направление 3 противоположно направлению вращения часовой стрелки.

Для определения ускорения какой-либо точки E , лежащей на оси звена BC , воспользуемся условием пропорциональности, аналогично определению скорости.

aEB lEB ; a (eb) lEB , aCB lCB a (cb) lCB

откуда (eb) (cb) lEB .

lCB

Отложив полученный отрезок (eb) на плане и соединив точку e с точкой , получим отрезок ( e ), изображающий в масштабе а абсолютное ускорение точки E ,

т.е. aE a ( e).

Для ускорения произвольной точки F , жестко связанной со звеном 3, можно воспользоваться теоремой подобия, рассмотренной при построении плана скоростей. Для этого строим на отрезке (cd ) плана ускорений тре-

угольник cdf , подобный треугольнику CDF на схеме. При обходе контура cdf в каком-либо направлении поря-

док букв должен совпадать с порядком букв контура CDF . Векторы абсолютных ускорений всех точек звеньев имеют своим началом точку – полюс плана ускоре-

33