Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский биотехнологический университет (РОСБИОТЕХ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TMM / Учебное_пособие_ТММ_МГУПБ.pdf

Скачиваний:

491

Добавлен:

09.04.2015

Размер:

3.42 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 2929

где rH – радиус водила;

r1 , r2 , r2 и r3 – радиусы начальных окружностей соответственно 1, 2, 2' и 3 колес.

Так как r mz2 , то в случае одинаковых моду-

лей обеих пар колес условие соосности можно записать так:

где

			z3 ,
		z1 z2 z2
z1, z2		z3 – числа зубьев колес.
	, z2 и
Для схемы на рис. 66, б по условию соосности
rH r1	r2		или r1 r2
		и rH r2 r3		r2 r3 ,
r1 , r2 , r2		и r3 – радиусы начальных окружностей

соответствующих колес.

В случае одинаковых модулей обеих пар колес это условие можно записать соответственно:

				z3 ,
			z1 z2 z2	z3 ,
где		и	z3 – числа зубьев колес.
где	z1, z2 , z2	и	z3 – числа зубьев колес.

Следовательно, в соосном планетарном механизме можно произвольно выбирать числа зубьев трех колес, а число зубьев четвертого колеса определяют из условия соосности.

9.2. Условие соседства в планетарных механизмах

Обычно в планетарных механизмах для уменьшения нагрузок на зубья колес и для обеспечения условий динамической уравновешенности механизма устанавливают не один, а несколько сателлитов под равными углами. Сателлиты располагают в одной плоскости так, чтобы окружности вершин зубьев сателлитов не пересекались. Это и является условием соседства. Для соблюдения усло-

133

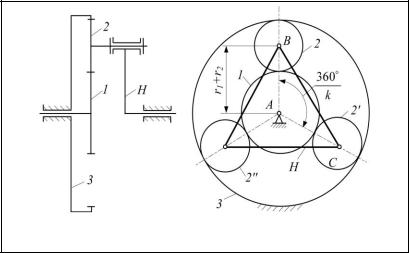
вия соседства (рис. 67) необходимо, чтобы выполнялось следующее условие:

BC da2 ,

где BC – расстояние между осями соседних сателлитов; da2 – диаметр окружности вершин зубьев сателли-

тов.

Рис. 67. К определению условия соседства сателлитов

	Из треугольника ABC имеем
	BC 2(r r ) sin		180		,
	BC 2(r r ) sin				,
	1	2		k
				k
где	r1 и r2 – радиусы начальных окружностей колес 1
и 2;
	k – число сателлитов.

Чтобы окружности вершин зубьев сателлитов не соприкасались, надо соблюсти неравенство

2(r r ) sin	180	d		.
			a2
1 2	k

Для зубчатых колес без смещения имеем

134

r1 mz2 1 , r2 mz2 2 , da2 m(z2 2) ,

откуда окончательно условие соседства примет вид

sin	180		z	2	2		или k	180				.
				2
	k		z		z				z2	2
		1				2		arcsin z		z
									1		2

9.3. Условие сборки в планетарных механизмах

При сборке планетарного механизма первый поставленный сателлит полностью определяет взаимное расположение центральных колес. Для того чтобы после этого между центральными колесами можно было вставить другие сателлиты, оси симметрии зубьев центральных колес 1 и 3 должны находиться на одной общей прямой. То есть необходимо соблюдать условие сборки, которое в соответствии с рис. 67 можно записать так:

k (z1 z3 ) , q

где k – ряд возможных значений для числа сателлитов; z1 и z3 – числа зубьев центральных колес;

q – целое число.

Поясним проверку условий соседства и сборки на следующем примере.

Пусть z1 = 20, z2 = 25, а z3 = 70. Из условий сосед-

ства k	180					180	4,87 . То есть чис-
ства k	arcsin	z1	2			arcsin 0,6	4,87 . То есть чис-
	arcsin	z	z	2
		z	z
		1			быть 4.
ло сателлитов		должно			быть 4.		Из условий сборки

135

k	(z1 z3 )	20 70	90	. Но числа	k и q должны
	q	q	q

быть целыми, тогда последнее условие при выборе, например, числа сателлитов k 4 удовлетворено не будет, так

как в этом случае q 90k 904 22,5 . Условию сборки

удовлетворяет число сателлитов k 3. При этом q 30 ,

т.е. – целое число.

Таким образом, при проектировании (синтезе) планетарной передачи необходимо выполнить условия соосности, соседства и сборки.

Библиографический список

1.Артоболевский И.И. Теория механизмов и машин : учебник для втузов / И.И. Артоболевский. – М. : Высш. шк., 1975. – 750 с.

2.Артоболевский И.И. Теория механизмов и машин: учебник для втузов / И.И. Артоболевский. – М. : Наука,

1988. – 640 с.

3.Заблонский К.И. Теория механизмов и машин: учебник / К.И. Заблонский, И.М. Белоконев, Б.М. Щекин.– Киев : Выща шк. Головное изд-во, 1989.– 376 с.

4.Фролов К.В. Теория механизмов и машин : учебник для вузов / К.В. Фролов, С.А. Попов, А.К. Мусатов [и др.]; под общ. ред. К.В. Фролова. – М. : Высш. шк., 2003. – 496 с.

136

	Содержание
Введение	...................................................................................3

1.Основные понятия и определения, принятые в теории

механизмов и машин ...............................................................	4
1.1. Звено механизма............................................................	4
1.2. Кинематическая пара ....................................................	4
1.3. Кинематическая цепь....................................................	5
1.4. Механизм .......................................................................	6
1.5. Машина ..........................................................................	6
2. Структура и классификация механизмов .....................	7
2.1. Классификация кинематических пар ..........................	7
2.2. Условное изображение кинематических пар ............	7
2.3. Степень свободы кинематической цепи и степени
подвижности механизма......................................................	9
2.4. Замена в плоских механизмах высших пар
низшими..............................................................................	11
2.5. Структурная классификация плоских механизмов .13
2.6. Группы Ассура второго класса ..................................	15
2.7. Определение класса механизма .................................	16

3.Кинематический анализ плоских рычажных

механизмов с низшими парами ............................................	17
3.1. Рычажные механизмы ................................................	18
3.2. Построение плана положений механизма ...............	20
3.3. Построение кинематических диаграмм ...................	22
3.4. Построение планов скоростей и ускорений ............	24
3.5. Определение скоростей и ускорений механизма
первого класса ....................................................................	24
3.6. Определение скоростей группы Ассура второго
класса первого вида ...........................................................	27
3.7. Определение ускорений группы Ассура второго
класса первого вида ...........................................................	30
3.8. Определение скоростей группы Ассура второго
класса второго вида ...........................................................	34

137

	3.9. Определение ускорений группы Ассура второго
	класса второго вида ...........................................................	35
	3.10. Кинематический анализ механизмов
	аналитическим методом ....................................................	37
	3.10.1. Аналоги скоростей и ускорений......................	38
	3.10.2. Кинематический анализ кривошипно-
	ползунного механизма аналитическим методом .......	41
4.	Динамический анализ механизмов..............................	45
	4.1. Движение механизмов под действием
	приложенных сил ...............................................................	46
	4.2. Определение закона движения механизма ..............	46
	4.3. Приведение сил и масс в механизмах .......................	48
	4.4. Уравнение движения механизма в энергетической
	форме...................................................................................	51
	4.5. Неравномерность движения механизмов и машин 52
	4.6. Уравнение движения машин для отдельных фаз....	53
	4.7. Средняя скорость машины и еѐ коэффициент
	неравномерного движения ................................................	55
	4.8. Назначение маховика..................................................	56
	4.9. Диаграмма энергомасс................................................	57
	4.10. Определение движения механизма по диаграмме
	энергомасс...........................................................................	59
	4.11. Определение момента инерции маховика .............	61
5.	Силовой анализ механизмов .........................................	65
	5.1. Определение сил инерции звеньев ............................	65
	5.2. Направление реакций в плоских кинематических
	парах ....................................................................................	67
	5.3. Условие статической определимости
	кинематических цепей.......................................................	69
	5.4. Определение реакций в кинематических парах
	группы Ассура второго класса первого вида ..................	70
	5.5. Определение реакций в кинематических парах
	группы Ассура второго класса второго вида ..................	73
	5.6. Силовой расчет ведущего звена ................................	76

138

5.7.	Рычаг Жуковского.......................................................	79
5.8.	Уравновешивание вращающихся масс .....................	81

6.Кинематический анализ механизмов с высшими

парами .....................................................................................		86
6.1.	Плоские кулачковые механизмы ..........................	86
6.2.	Механизмы зубчатых передач ..............................	89
6.3.	Планетарные механизмы.......................................	94
6.4.	Дифференциальные механизмы ...........................	96
7. Синтез кулачковых механизмов .................................		100
7.1. Кинематическая схема механизма...........................		100
7.2. Циклограмма работы механизма .............................		100
7.3. Закон движения толкателя на фазах подъема и
опускания ..........................................................................		102
7.4. Угол давления в кулачковых механизмах ..............		104
7.5. Определение угла давления по заданному закону
движения толкателя и минимального размера кулачка105
7.6. Выбор радиуса ролика ..............................................		109
8. Синтез трехзвенных зубчатых передач с
неподвижными осями ..........................................................		111
8.1. Основная теорема зацепления .................................		112
8.2. Эвольвента окружности и еѐ свойства...................		116
8.3. Уравнение эвольвенты..............................................		117
8.4. Эвольвентное зацепление.........................................		119
8.5. Методы изготовления эвольвентных профилей
зубьев.................................................................................		121
8.6. Основные элементы эвольвентного зацепления ....		125
8.7. Подрезание профилей зубьев...................................		128
8.8. Зубчатые колеса со смещением ...............................		129
9. Синтез зубчатых передач с подвижными осями.......		132
9.1. Условие соосности в планетарных механизмах.....		132
9.2. Условие соседства в планетарных механизмах .....		133
9.3. Условие сборки в планетарных механизмах .........		135
Библиографический список ................................................		136

139

Учебное издание

Комляков Герман Алексеевич Маркус Леонид Ильич

ТЕОРИЯ МЕХАНИЗМОВ И МАШИН

Учебное пособие для студентов специальностей

260601, 260602, 140504, 190603 очного обучения и ФБО

Редактор И.А. Мырсина

Подписано в печать 28.02.08. Усл. печ. л. 8,5. Тираж 200 экз. Заказ 8/30. Изд. № 5.

МГУПБ. 109316. Москва, ул. Талалихина, 33.

ООО "Полисувенир"109316. Москва, ул. Талалихина, 33. Тел. 677-03-86

140

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 2929

Соседние файлы в папке TMM

#
09.04.2015120.84 Кб20Библиографический список.pdf
#
09.04.20151.49 Mб192Лекции_по_ТММ_ОМСК.pdf
#
09.04.2015122.28 Кб22Прочти_меня.pdf
#
09.04.20153.42 Mб491Учебное_пособие_ТММ_МГУПБ.pdf