Так как о характере движения толкателя по кривой перемещения S f (t) судить затруднительно, то обычно

задают диаграмму его ускорения a f (t) .

Диаграмму перемещения S f (t) , необходимую для построения профиля кулачка, получают методом двукратного интегрирования диаграммы ускорения a f (t) .

7.4. Угол давления в кулачковых механизмах

Для эффективной работы кулачкового механизма важно обеспечить высокий КПД и отсутствие заклинивания. Угол давления позволяет выявить эти условия его работы.

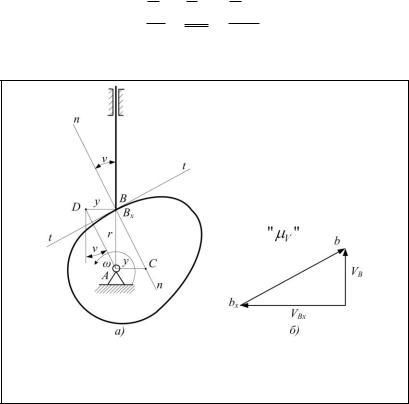
Углом давления в кулачковых механизмах называют угол между общей нормалью к профилю кулачка в точке касания толкателя и направлением движения (скорости) толкателя (рис. 53).

Рис. 53. Угол давления в кулачковом механизме

104

Сила давления кулачка на толкатель F (без учета сил трения) направлена по нормали к профилю кулачка.

Под действием движущей силы F cos толкатель поднимается и преодолевает силы полезных сопротивлений и силы трения в направляющих толкателя.

Сила вызывает перекос толкателя и возникновение сил трения в направляющих толкателя. Если эта сила велика, то может произойти заклинивание и поломка толкателя.

Для уменьшения силы выгодно, чтобы угол давления был как можно меньше.

Однако, с другой стороны, с уменьшением угла возрастают размеры кулачка, что нежелатель-

Учитывая вышеизложенное, при проектировании кулачковых механизмов устанавливают максимальное зна-

чение угла давления max , которое не должно быть пре-

взойдено, так как в противном случае возникают большие силы трения, снижается КПД кулачкового механизма и возможны заклинивание и поломка толкателя.

На практике значения угла давления max прини-

мают равными: 30° – для поступательно движущихся толкателей; 45° – для качающихся толкателей (коромысел).

7.5. Определение угла давления по заданному закону движения толкателя и минимального размера кулачка

Как было отмечено, выбор угла давления влияет на размеры кулачка. Из конструктивных соображений всегда желательно выбрать кулачок возможно меньших размеров, т.е. с минимальным радиусом R . Поэтому при построении профиля кулачка нужно обеспечить, с одной стороны, что-

бы угол давления не превосходил max , а с другой, чтобы

105

кулачок имел минимальные размеры. Для этого необходимо до построения профиля кулачка по известным параметрам уметь определять угол давления.

Рассмотрим определение угла давления , если

известны закон движения толкателя и положение оси вращения кулачка (рис. 54, а).

Примем, что точка Bx принадлежит кулачку, а точка B – толкателю.

Тогда VBx r ,

где – угловая скорость кулачка;

r – расстояние точки Bx до оси вращения кулачка.

VB VBx VBBx .

Для решения этого векторного уравнения строим план скоростей в масштабе V (рис. 54, б).

Рис. 54. К определению угла давления в кулачковом механизме:

а – схема механизма; б – план скоростей

106

Проведем через ось вращения кулачка линию, перпендикулярную направлению движения толкателя, до пересечения с нормалью. Получим отрезок y AC .

Треугольники ABxC (на схеме механизма) и pbxb (на плане скоростей) подобны как треугольники с взаимно перпендикулярными сторонами. Из подобия сле-

B в направлении, перпендикулярном направлению движения толкателя (влево), и его конец (точку D ) соединить прямой линией AD с осью вращения кулачка (точкой A ), то угол между этой линией и направлением движения толкателя, как это видно из чертежа, равен углу давления .

Таким образом, для определения угла давления не нужно знать профиль кулачка. Достаточно вычислить по заданному закону движения толкателя значение величины отрезка y ( AC) , отложить этот отрезок от данного поло-

жения точки B толкателя в направлении, перпендикулярном направлению ее скорости, и соединить прямой линией конец отрезка с осью вращения кулачка. Угол между этой линией и направлением скорости точки B – угол давления. Отрезок y откладывают в сторону направления вектора

скорости точки B толкателя, если повернуть его на угол 90° по направлению вращения кулачка.

107

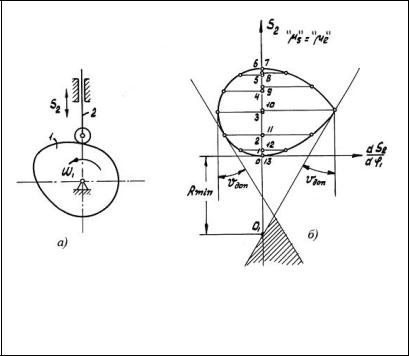
Для определения минимального радиуса кулачка по заданному движению толкателя определяют значение отрезка y для нескольких положений толкателя на фазах

подъема и опускания. Затем откладывают эти отрезки так, как было указано выше, и соединяют их концы плавными кривыми. Далее к этим кривым проводят касательные под заданными максимальными углами давления соответственно для фазы подъема и опускания толкателя (рис. 55).

Рис. 55. К определению минимального радиуса кулачка:

а – схема механизма; б – определение минимального радиуса кулачка Rmin

За центр вращения кулачка O1 можно принять лю-

бую точку, лежащую внутри заштрихованной области. В случае, когда ось толкателя проходит через центр враще-

ния кулачка, минимальный радиус Rmin получают пересечением оси толкателя с заштрихованной зоной.

108