6.3. Планетарные механизмы

Сателлитные зубчатые механизмы с одной степенью подвижности называют планетарными механизмами.

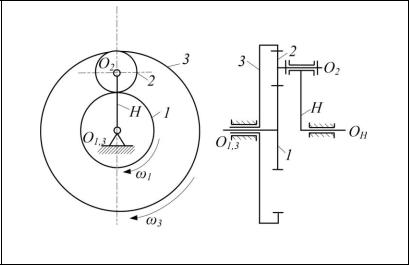
На рис. 49 показана схема одного из вариантов планетарного механизма, образованного из центрального колеса 1, сателлита 2, опорного колеса 3, водила H и стойки.

Рис. 49. Схема планетарного механизма

Степень подвижности подсчитывают по формуле

Чебышева:

W 3n 2 p5 p4 3 3 2 3 2 1,

т.е. данный механизм имеет одно ведущее звено (например, водило H ). Для определения передаточного отношения

u1H 1 механизма воспользуемся методом обращения

H

движения. Относительное движение звеньев не изменяется, если всем звеньям механизма сообщать дополнительное вращение с какой-либо общей угловой скоростью. Сообщим всем звеньям механизма дополнительное вращение

94

вокруг оси ОН с угловой скоростью – H , равной по ве-

личине, но противоположной по направлению угловой скорости водила H . Тогда звенья механизма будут иметь угловые скорости:

Следовательно, после сообщения звеньям механизма дополнительного вращения с угловой скоростью

– H звено H будет неподвижно, и планетарный меха-

низм превратится в обыкновенный зубчатый механизм с неподвижными осями.

через числа зубьев зубчатых колес 1, 2 и 3.

95

6.4. Дифференциальные механизмы

Сателлитные зубчатые механизмы с двумя и более степенями подвижности называются дифференциальными механизмами.

Из планетарного механизма, показанного на (рис. 49), может быть получен дифференциальный механизм, если опорное (неподвижное) колесо 3 сделать подвижным (рис. 50).

Рис. 50. Схема дифференциального механизма

Степень подвижности дифференциального меха-

низма

W 3n 2 p5 p4 3 4 2 4 2 2 .

96

Определить закон движения данного механизма можно, если иметь заданными законы движения двух зве-

ньев (например, 1 и 3 ). Для нахождения закона движения ведомого звена (например, H ) воспользуемся методом обращения движения.

Зная значения 1 , 3 и z1 , z3 , можно определить величину H .

Замкнутый дифференциальный механизм Если в дифференциальном механизме между ве-

дущими звеньями установлена промежуточная зубчатая передача, то такой дифференциальный механизм называют

97

замкнутым дифференциальным механизмом. Он имеет одну степень подвижности.

Пусть у механизма (рис. 51) колеса 1 и 3 связаны промежуточной зубчатой передачей, состоящей из колес 1, 2, 2`, 3. Вследствие этого угловая скорость колеса 3` зависит от угловой скорости ведущего звена 1.

Определим степень подвижности этого механизма:

W 3n 2 p5 p4 3 5 2 5 4 1.

Так как степень подвижности такого дифференциального механизма равна единице, механизм имеет одно ведущее звено.

Рис. 51. Схема замкнутого дифференциального механизма

Для определения общего передаточного отношения механизма u1H воспользуемся формулой

98

99