
- •Московский Государственный Университет Пищевых Производств е.И. Конопленко Сборник задач
- •Оглавление
- •Введение
- •Линейные процессы
- •Разветвляющиеся вычислительные процессы
- •Циклические процессы Табулирование ф-ций, нахождение максимума и минимума.
- •Табулирование ф-ций двух переменных
- •Вычисление сумм, произведений
- •Сложные циклы
- •Табулирование функции, нахождение min, max.
- •Одномерные массивы
- •Двумерные массивы
Вычисление сумм, произведений
|
№
|
Вычислить сумму |
Вычислить произведения |
| |
|
1 |
2 |
3 |
| |
|
1 |
Y= |
|
| |
|
2 |
Y= |
Z= |
| |
|
3 |
Y= |
Z=3siny+ |
| |
|
4 |
Y=ln( |
Z= |
| |
|
5 |
Y= |
Z=sin |
| |
|
6 |
Y
=
|
Z
= arctg x + |
| |
|
7 |
Y= |
Z= |
| |
|
8 |
Y= |
Z=cos |
| |
|
9 |
Y= |
Z= |
| |
|
10 |
Y=arctg |
Z=
x |
| |
|
1 |
2 |
3 |
|
11 |
Y= |
Z=y3+ |
|
12 |
Y=cos
x+ |
Z= |
|
13 |
Y= |
Z= |
|
14 |
Y= |
Z= |
|
15 |
Y=cos |
Z= |
|
16 |
Y= |
Z= |
|
17 |
Y= |
Z= |
|
18 |
Y= |
Z=arctg |
|
19 |
Y=ln
x+2 |
Z= |
|
20 |
Y= |
Z= |
|
1 |
2 |
3 |
|
21 |
Y=ln |
Z= |
|
22 |
Y
=
|
Y= |
|
23 |
Y
=
|
Z
= |
|
24 |
y |
Z=
|
|
25 |
Y=lnx |
Z= |
|
26 |
Y
=
|
Z
= y +
|
|
27 |
Y
= lnx |
Z
= |
|
28 |
Y
=
|
Z
= lny |
|
29 |
Y
=
|
Z= |
|
30 |
Y=cos |
Z= |
|
1 |
2 |
3 |
|
31 |
Y= |
Z=sin |
|
32 |
Y=sinx+2ln |
Z= |
|
33 |
Y= |
Z=y+ |
|
34 |
Y= |
Z= |
|
35 |
Y= |
Z=ln |
Сложные циклы
Табулирование функции, нахождение min, max.
-
№ вар.
Функция
Начальн. значение
Конечн. значения
Шаг
1
2
3
4
5
1
Х
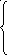 2
+
2
+
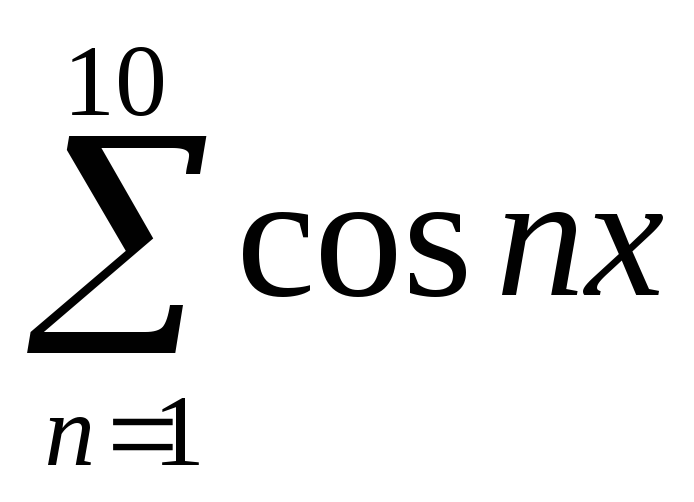 если х
3
если х
3Y = х + 3 tg2x если 4 х 5
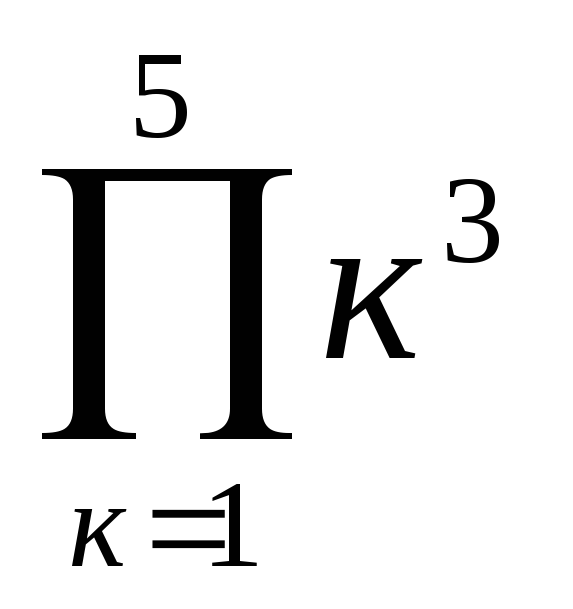 +
ех
если х
6
+
ех
если х
6х =
 + 2 ab + cos a
+ 2 ab + cos a1
3
0.2
2
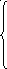 y
+
y
+
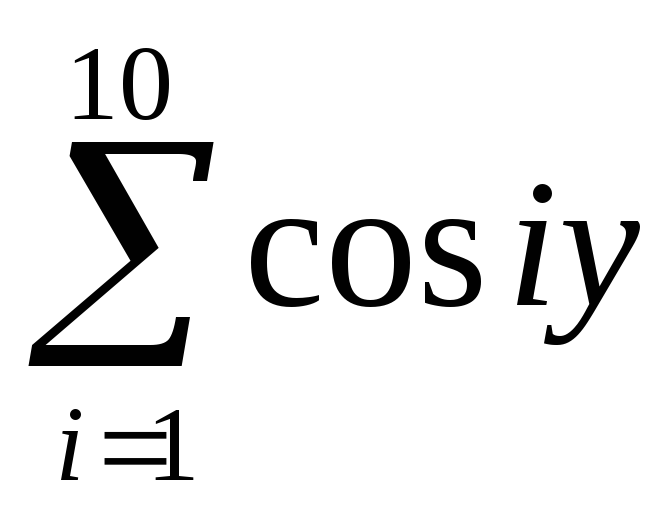 если у
3
если у
3Z =
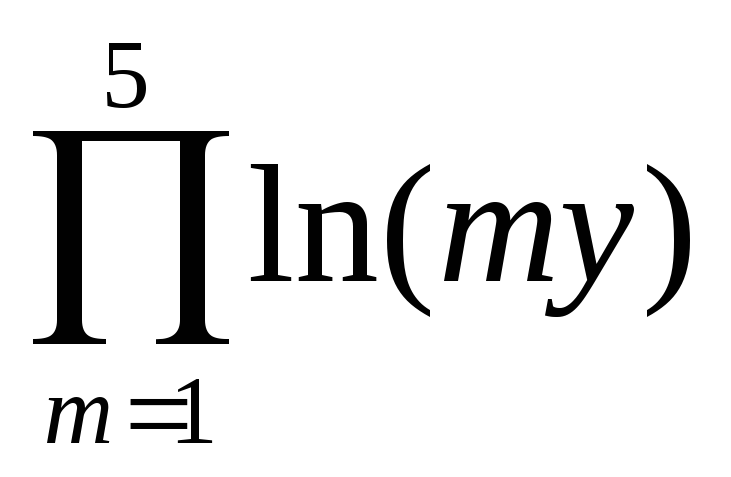 +
y
если 4
у
5
+
y
если 4
у
5у +3 если у 7
у = х5 + 2х - cos x
1
5
0.5
3
е
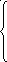 у
+
у
+
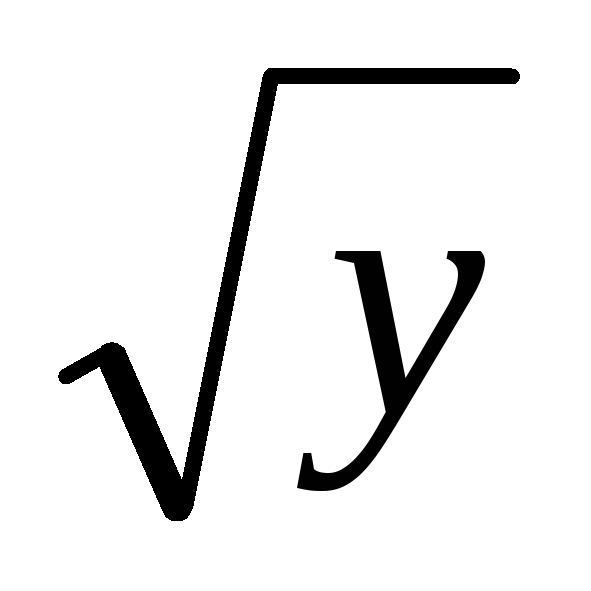 если у
2
если у
2Z =
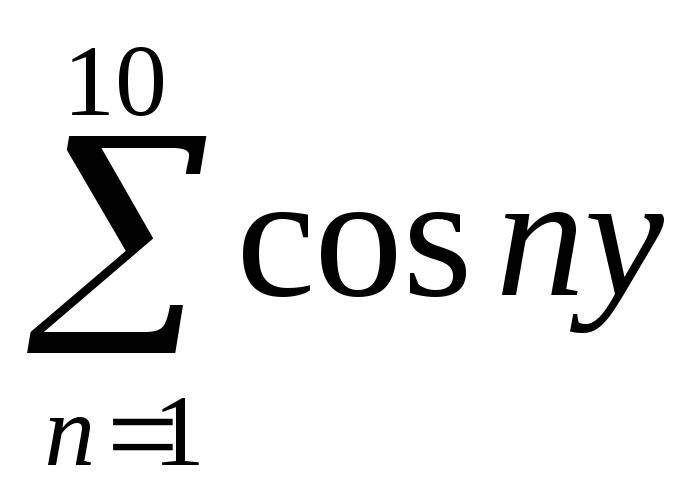 если 3
у
4
если 3
у
4 У3 +
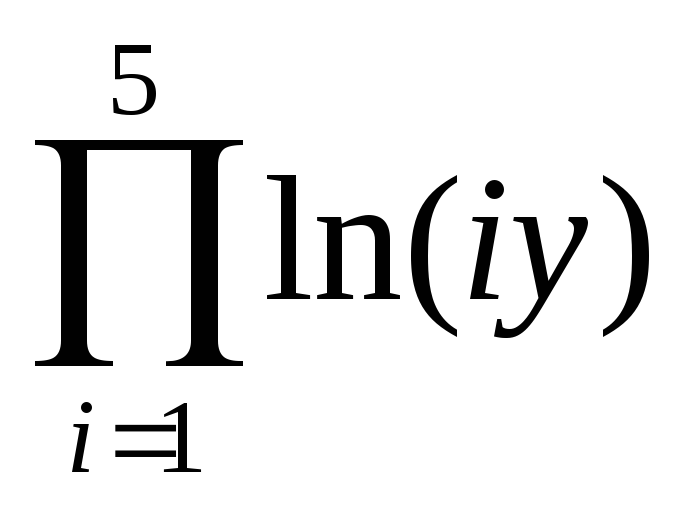 если у
5
если у
5У =
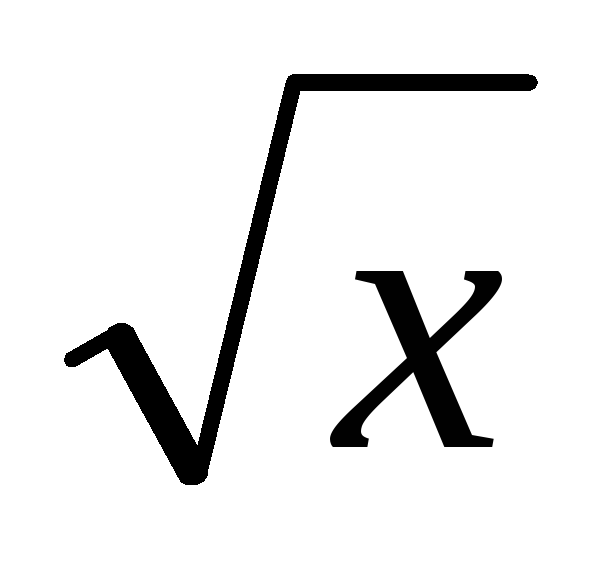 + 2 х2
- 3 tg
x
+ 2 х2
- 3 tg
x1
3
0.5
4
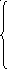 Y5
+
y
+
Y5
+
y
+
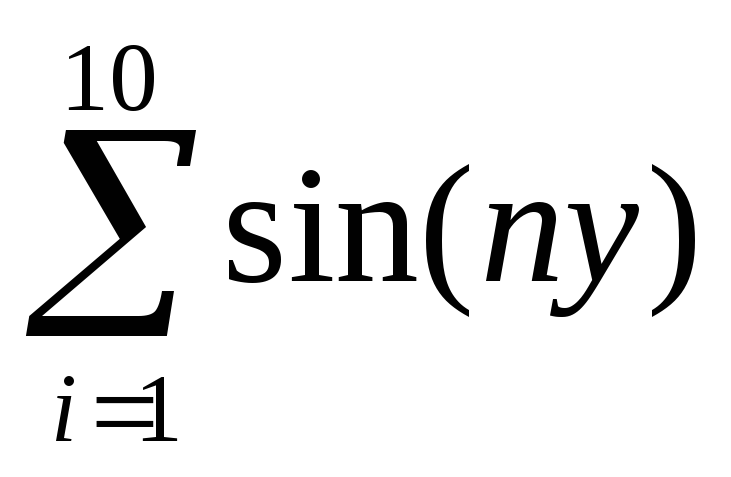 если у
5
если у
5 Z =
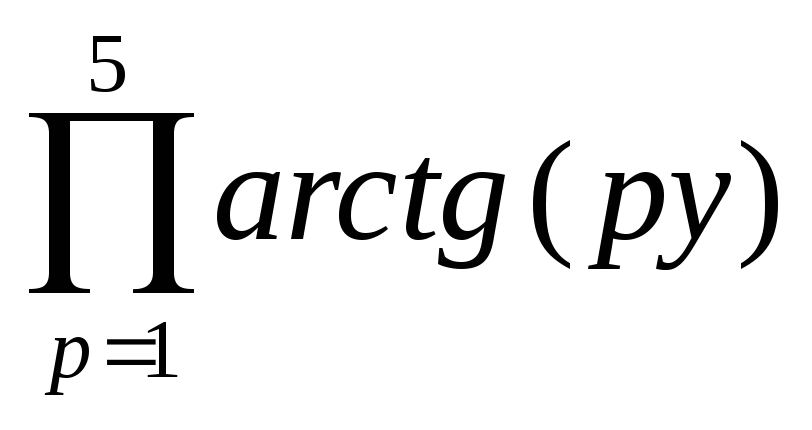 если 6
у
7
если 6
у
7 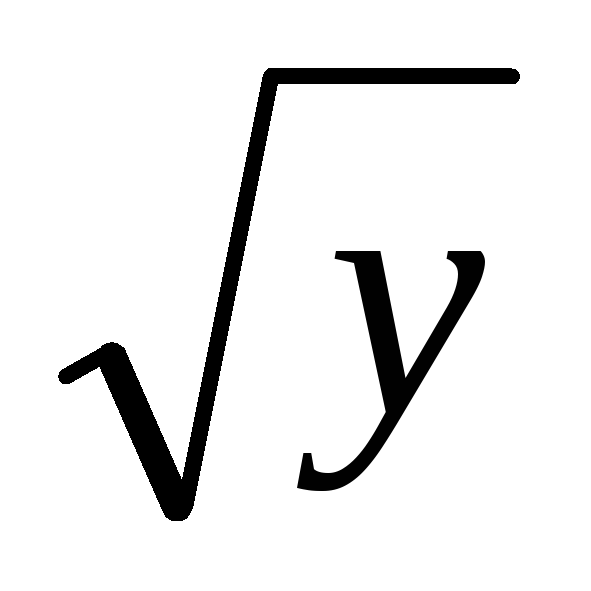 + 2 cos3
y
если у
5
+ 2 cos3
y
если у
51
5
0.5
5
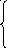 X
3 +
X
3 +
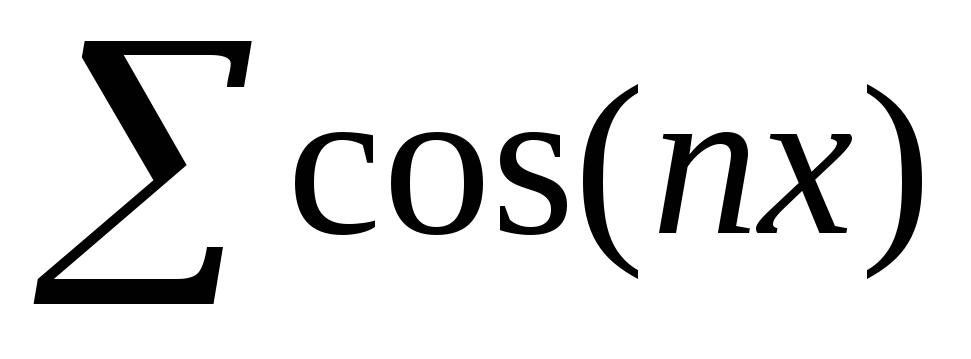 + 3 если х
6
+ 3 если х
6У =
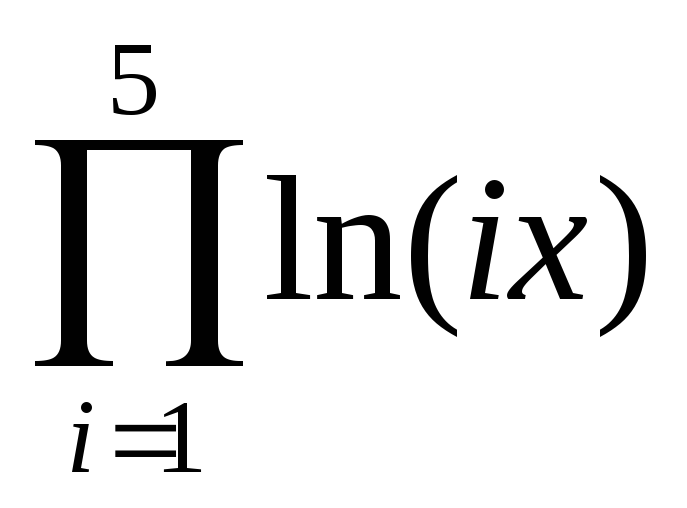 +
+
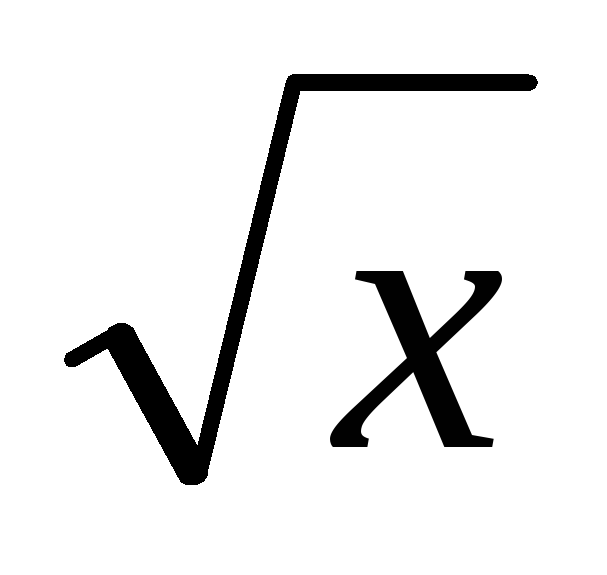 если 7
у
12
если 7
у
12Cos2 x - sin x2 если х 13
X = t3 + et +2 sin t
1
5
0.5
|
6 |
Y=sinx3+
lnx- 3 если х20
х = а + а2– 3 |
2 |
5 |
0,3 |
|
7 |
y=cos sinx2- 3 если х20
x= 0,2 +t+ |
3 |
10 |
0.5 |
|
8 |
Z=y3+ lny+ 2 , если у10
y= x2 + 2 sin x +0.5 |
0.1 |
10.1 |
0.1 |
|
9 |
X
Y=cos
Lnx+2 , если х7
Z = arctg y + 2 y2 –3 |
1 |
10 |
0.2 |
|
10 |
Y=cosx2+
Lnx–3 , если х6
Z=y3+ 2 |
1 |
10 |
0.5 |
|
11 |
Z=ln|x|
+
Х +
X=a3- 5 |
1 |
10 |
0.5 |
|
12 |
L Z=cosx3+ 2 , если 4х5
y=z2+ 3 |
2 |
10 |
0.5 |
|
13 |
X Y=x3+
Cosx3, если х10
Z = y3 + sin2 y |
2 |
12 |
0.5 |
|
14 |
Y Z=cosy+ 2 , если 5
Θ = z3+ 2 |
2 |
10 |
0.5 |
|
15 |
x=
arctga+ 3 , если а > 7
y
= x5
+ sin
|
1 |
10 |
0.5 |
|
16 |
X Z=cosx+ 3x3, если 5 <x< 6
y=z5+ 2lnz
|
2 |
8 |
0.2 |
|
17 |
x = ln a + a2 –3 , если 5 < a <7 cos a3 , если a > 7
y = x5 + 2 ln x |
2 |
10 |
0.5 |
|
|
Z = y5 + 2 sin y - 3 X3+cosx+2 если х3 Y=
|
1.5 |
10.5 |
0.5 |
|
|
Q=z+ 2
y+5 если у2 Z= у3+ Sin 2y + cos y2 если y 7
|
1 |
10 |
0.5 |
|
|
Y=x5 + 2 a2+ 3 если а2 x=
sin2 a если a 10 |
3 |
15 |
0.5 |
|
|
Z=y5+ 2 Sin2+ 2 если х5 Y = sin x + ln x если 7 x 8
|
3 |
15 |
0.5 |
|
|
x2 + 3lnxесли х2
Z=
X+ 5 еслиx7 Y
= z5
+
|
2 |
10.5 |
0.5 |
|
|
Z = y5
+ 2 y +
x2+ 2lnxесли х2 y=
x+ 5 еслиx10
|
2
|
10.5
|
0.5
|
|
|
T=sin
x2+ 2sinxесли х2 Y=
lnx2еслиx10
|
1 |
15 |
0.5 |
|
|
Q = ln ( Sin y + 2 y если y 2 Z=
arctgyеслиy5
|
|
|
|
|
|
x+
Z=
y
= z2
+ 5
|
3 |
15 |
0.8 |
|
|
Z = y5
+ 2 sin y +
Y=x3+
Sin2x + cos x2 если 5 y 7 |
0.5 |
7.5 |
0.8 |
|
|
Q = cos ( Z = arctg y + 2 если 2 y 3
|
1.5 |
7.5 |
0.5 |
|
|
Z=y5+
2 lnx+x3если х3
Y=
arctg x x 7
|
2 |
3 |
0.5 |
|
30 |
Y=x+ 3, если 3 <x< 5
z = y3
+ 2 sin y - 3
|
1 |
6 |
0.5 |
|
31 |
Z=
y=z5 +
|
0.5 |
6 |
0.5 |
|
32 |
Ln|x| +x5–3, если х < 3 Y = arctg + 3 sin2 x , если 5 < x < 7
z=y5+ 3
|
2 |
12 |
0.5 |
|
33 |
z=
3 +
Θ=z3+2 |
2 |
8 |
0.5 |
|
34 |
Y=
Z=y3+
|
4 |
10 |
0.5 |
|
35 |
Y=
arctg(
Z = ln
|
0.5 |
6.5 |
0.5 |

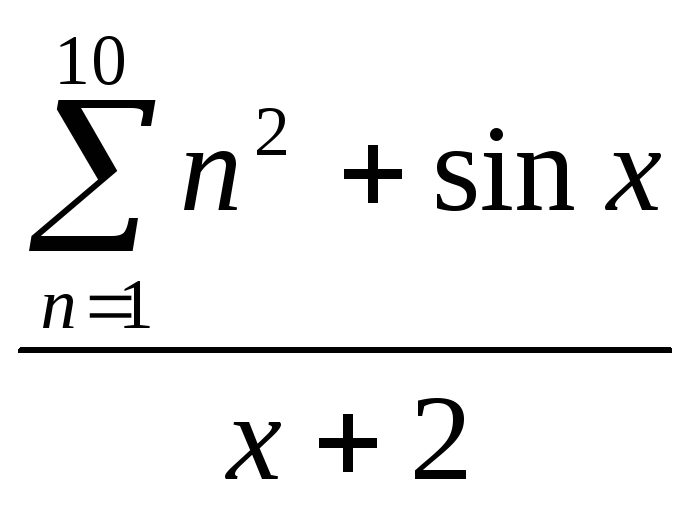
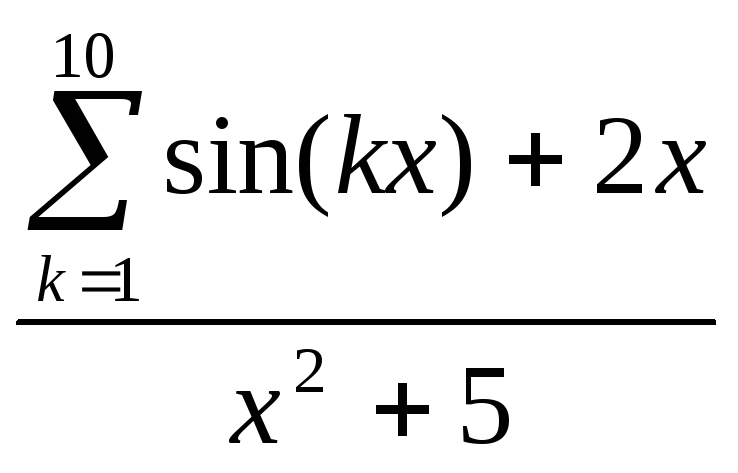
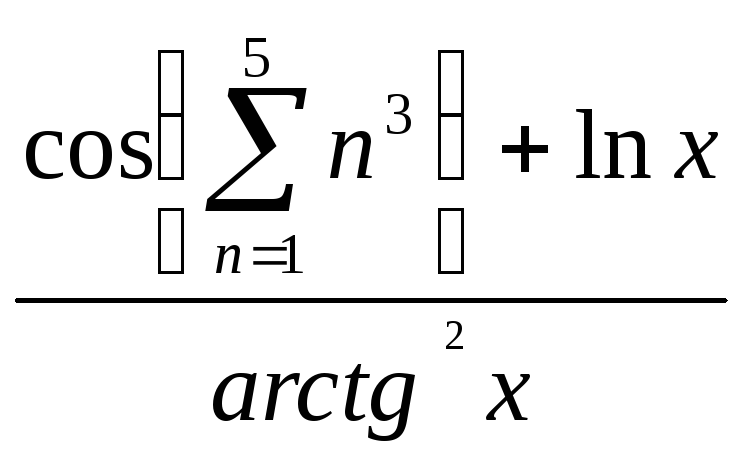
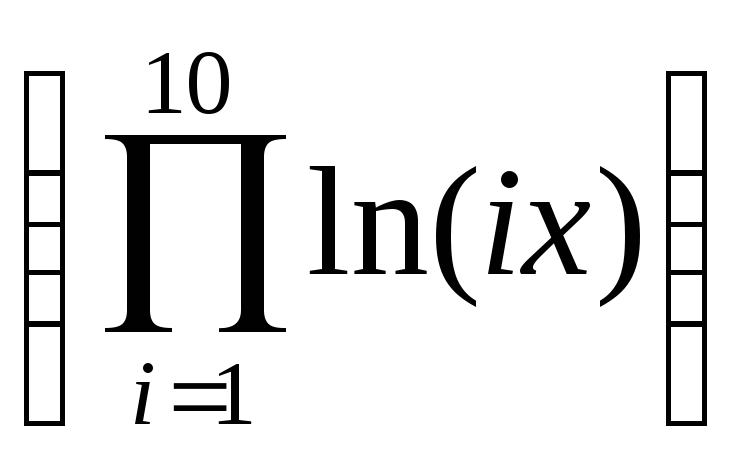
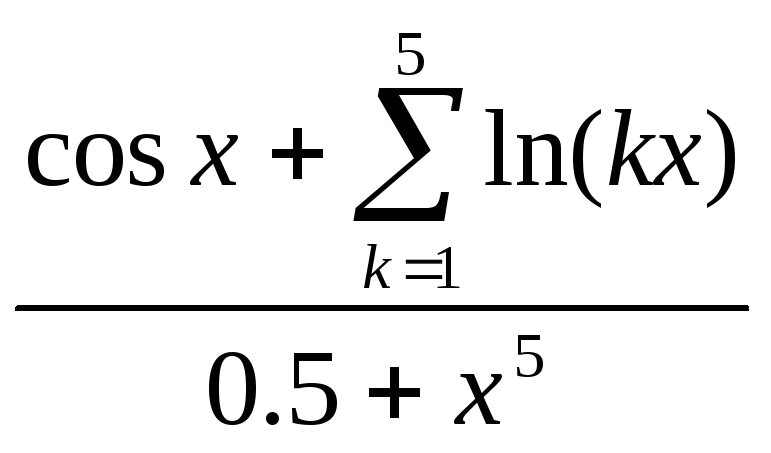
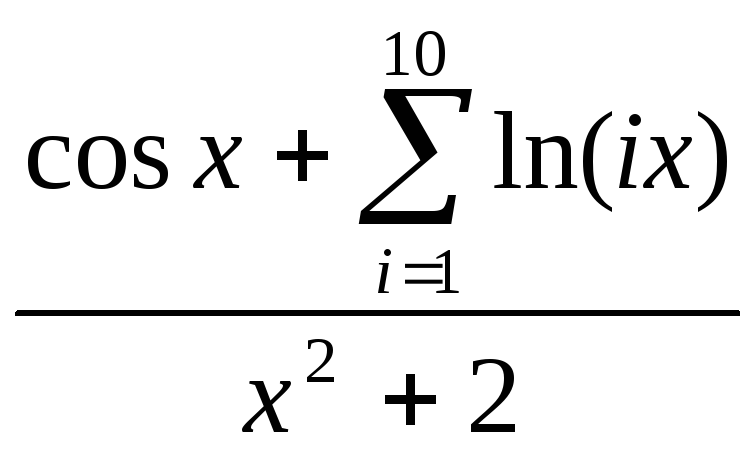
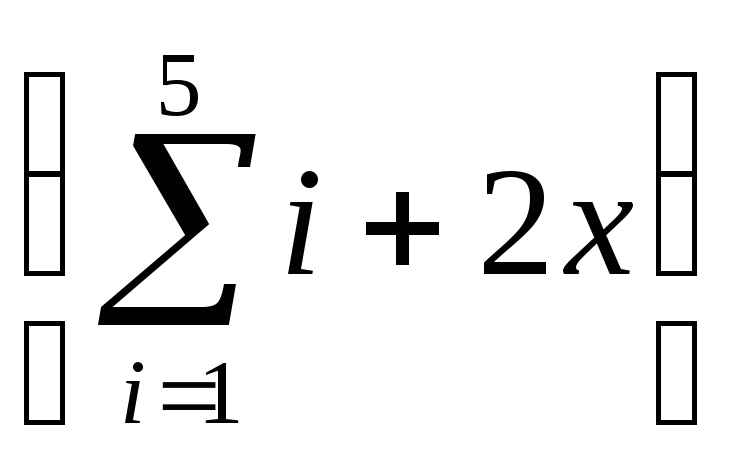
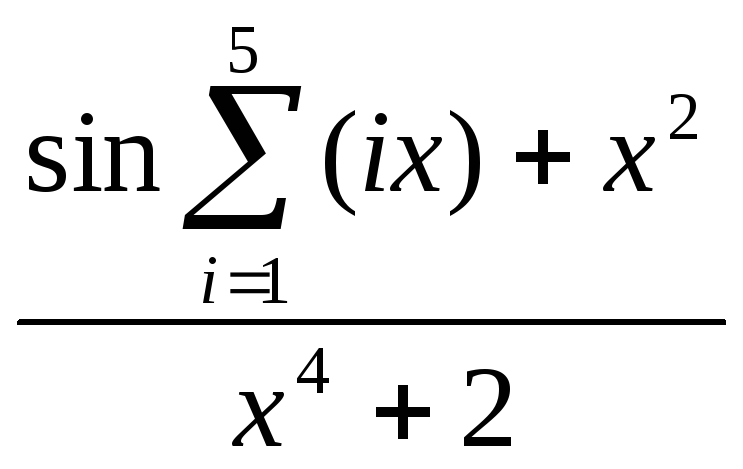
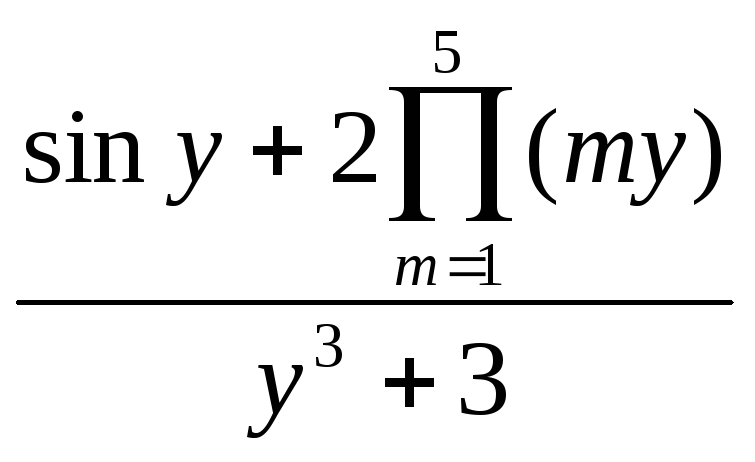
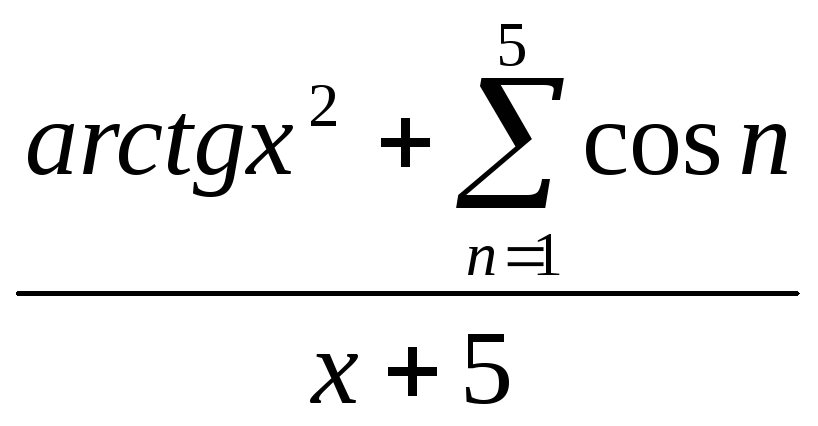
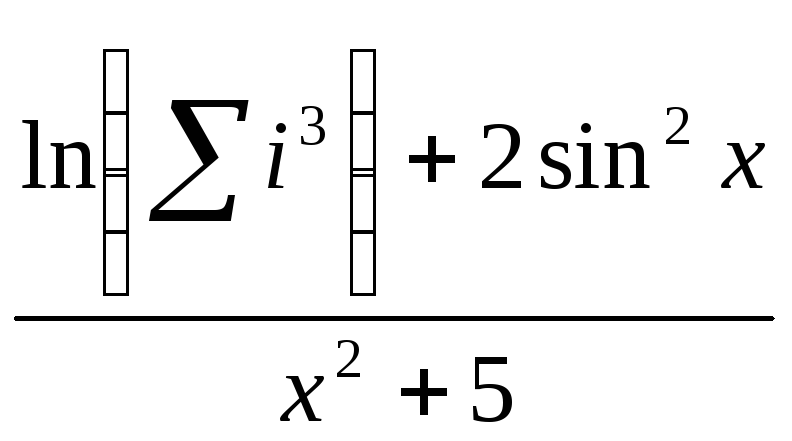
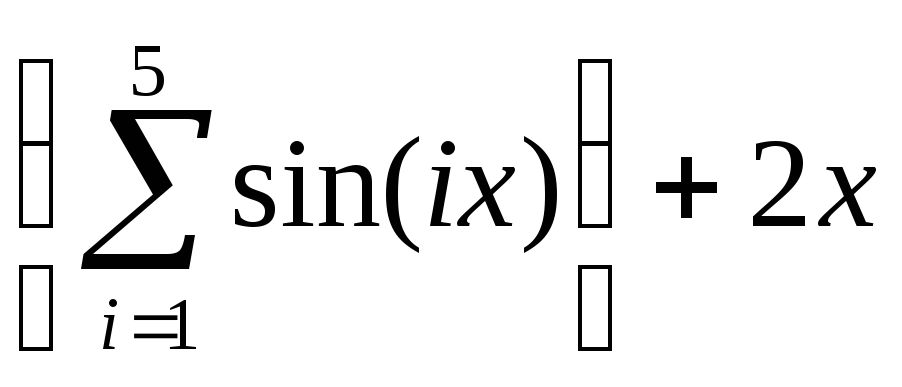
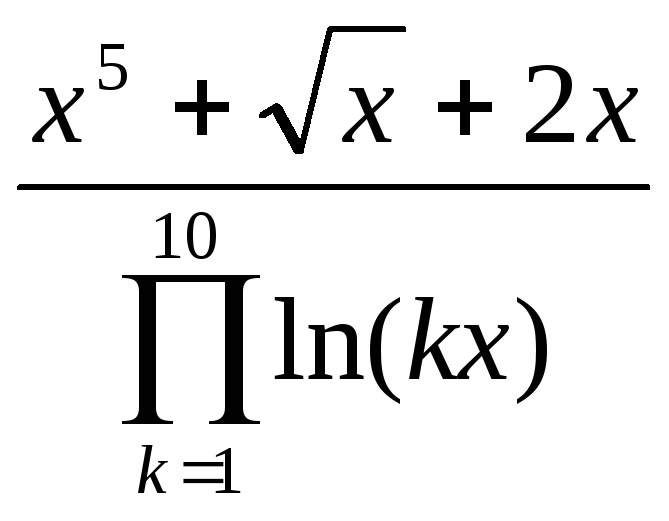
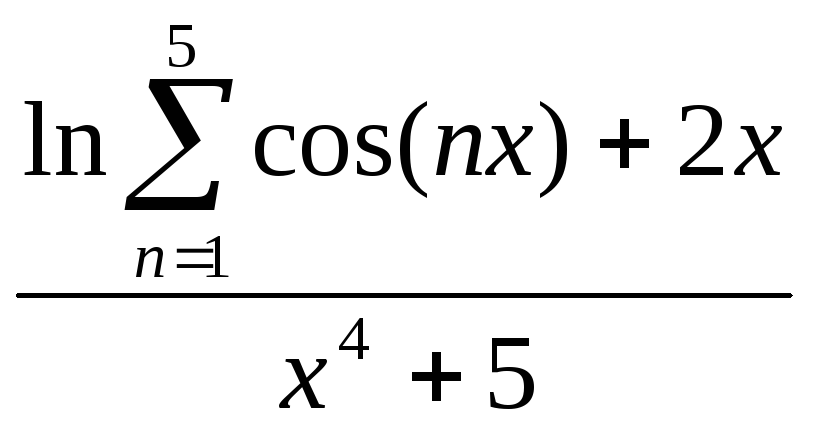
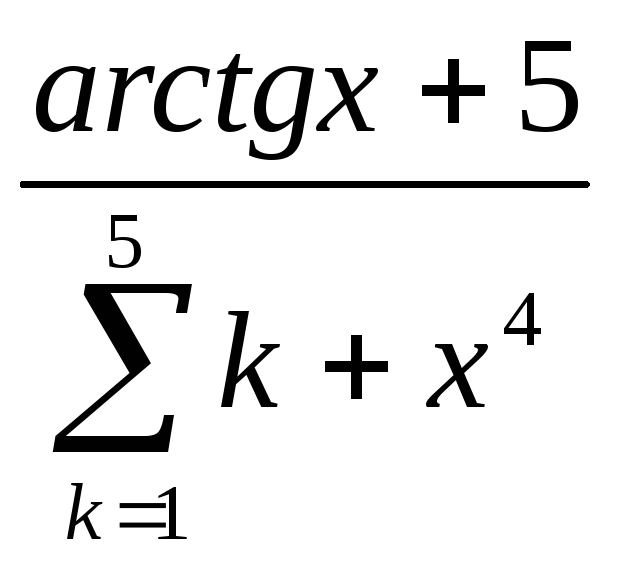

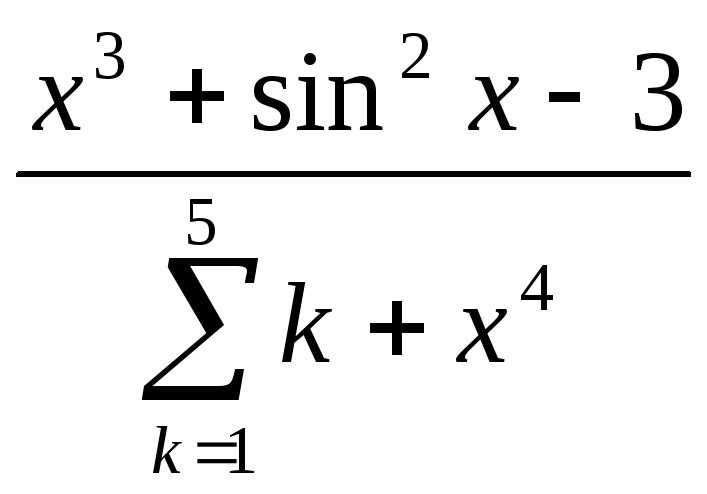
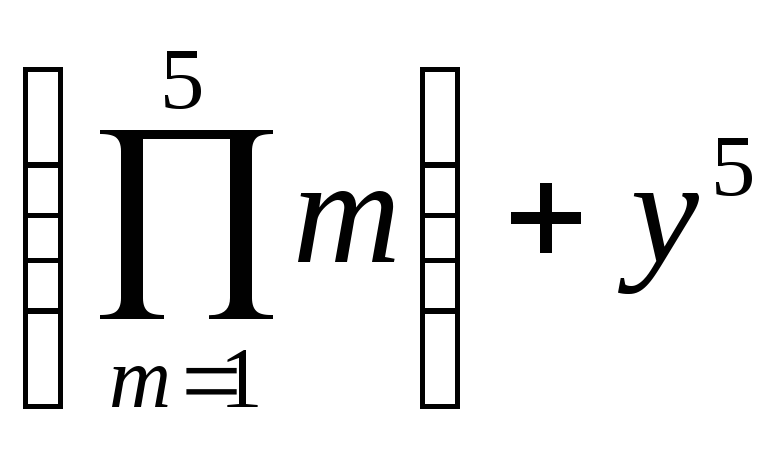
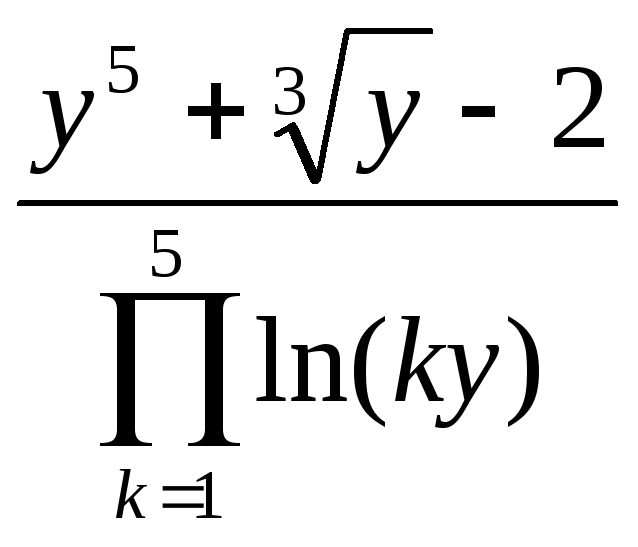
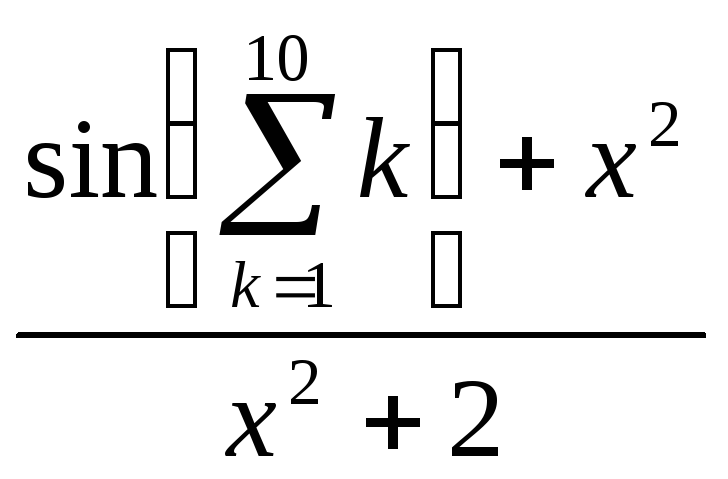
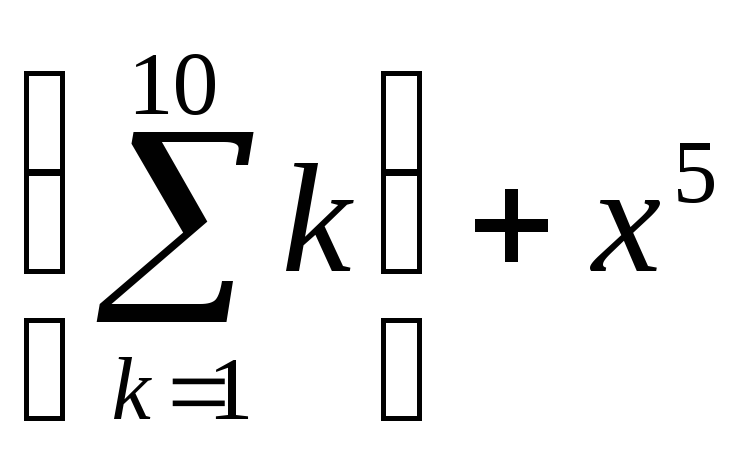
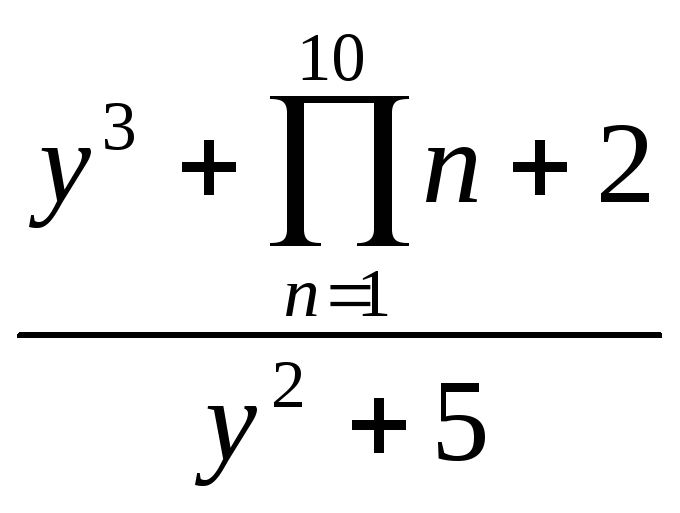
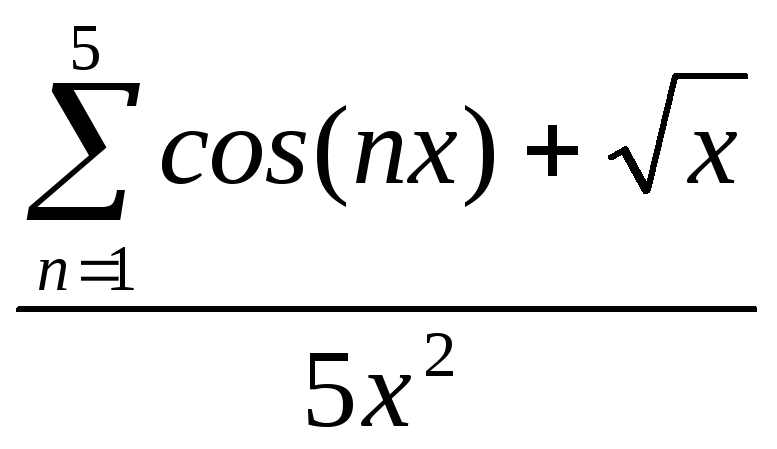
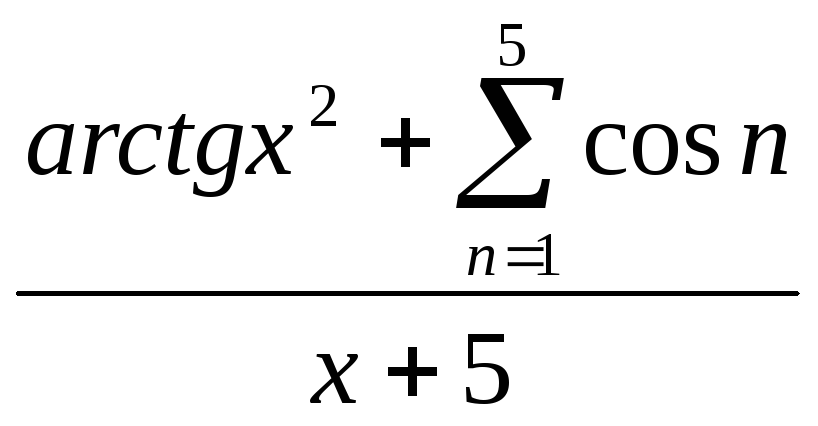
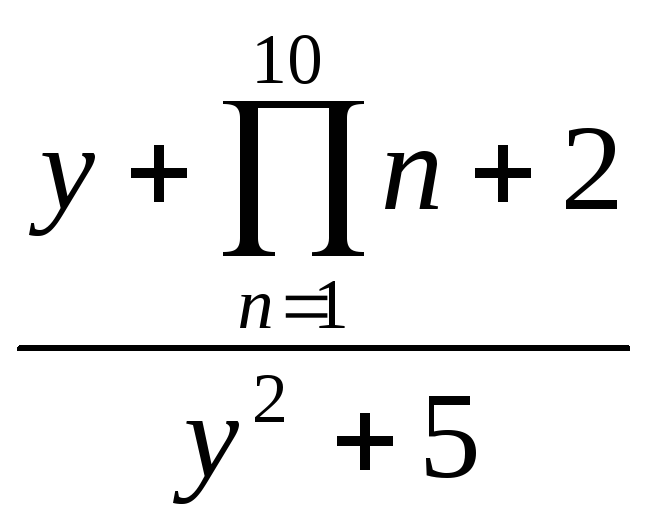
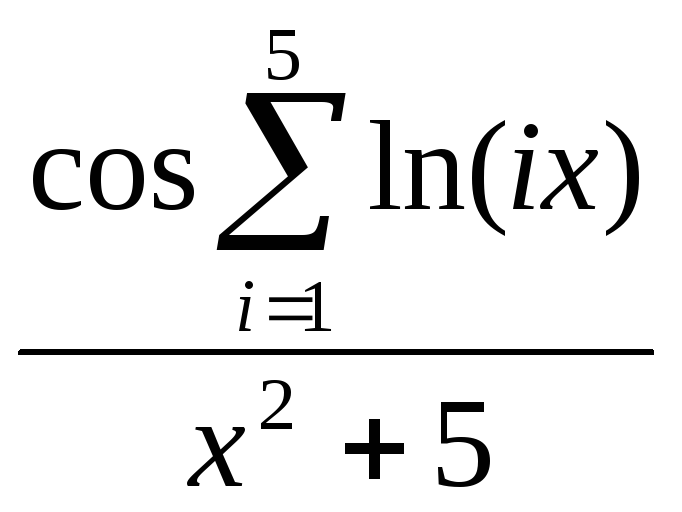
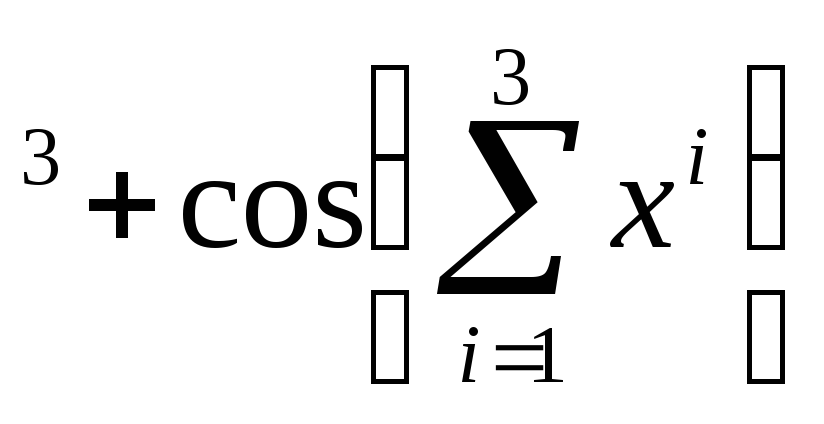

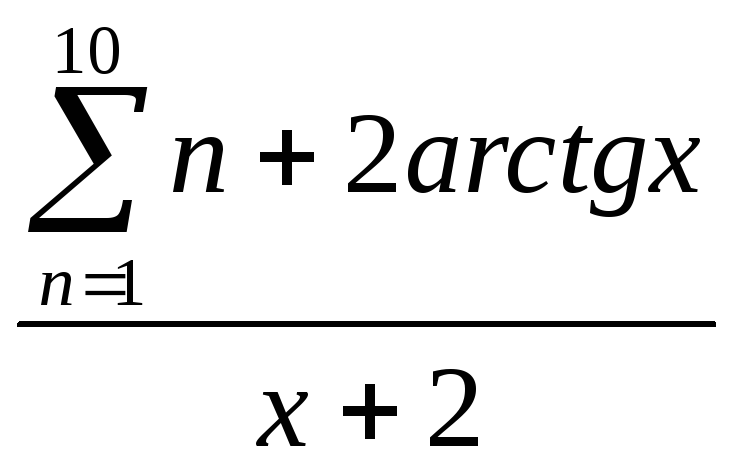
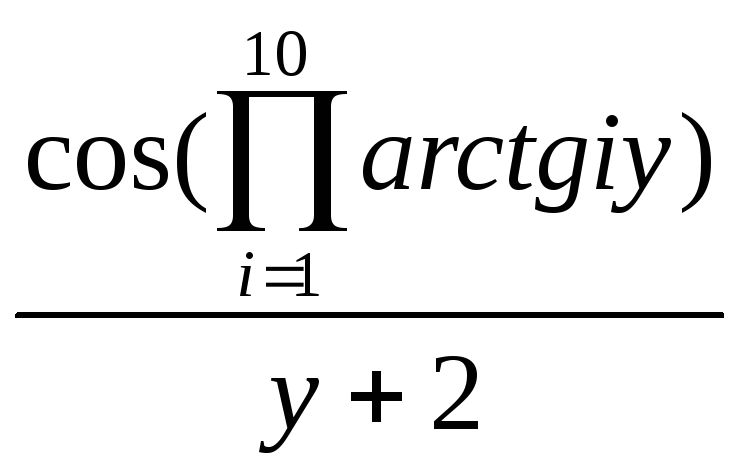
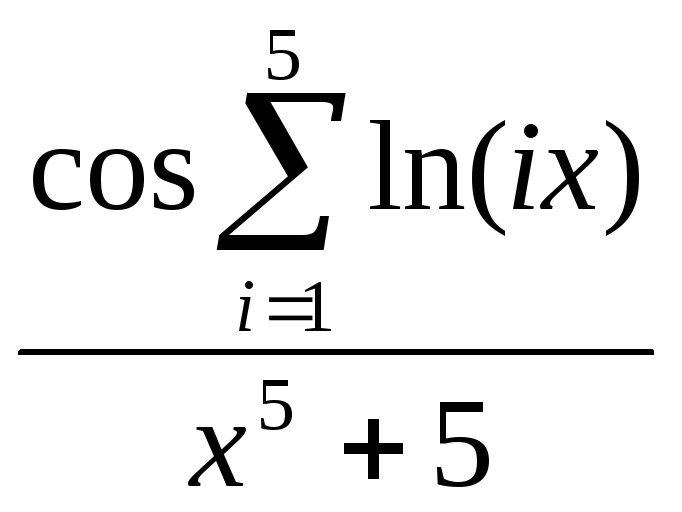
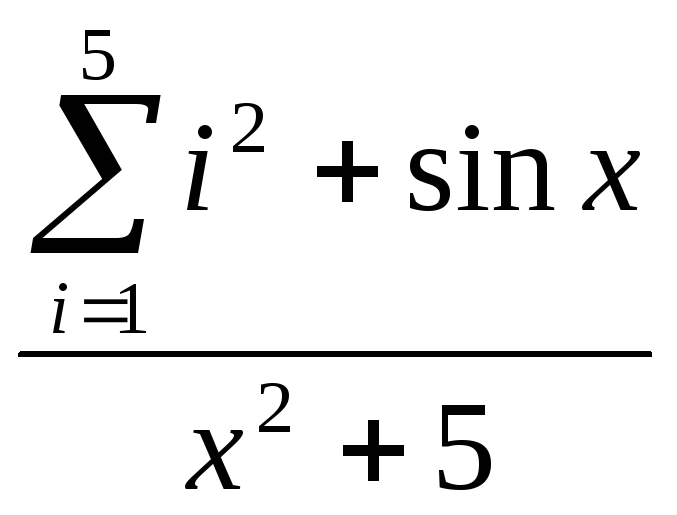
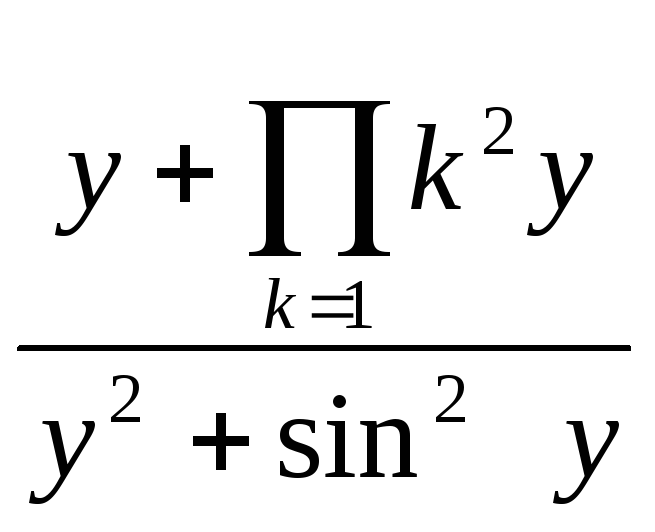
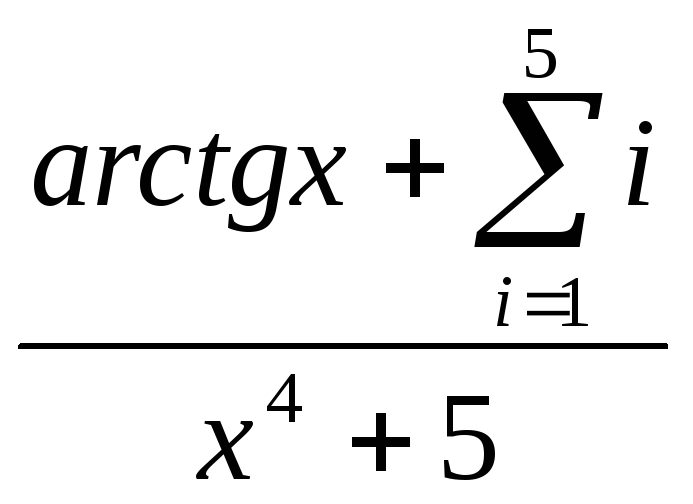
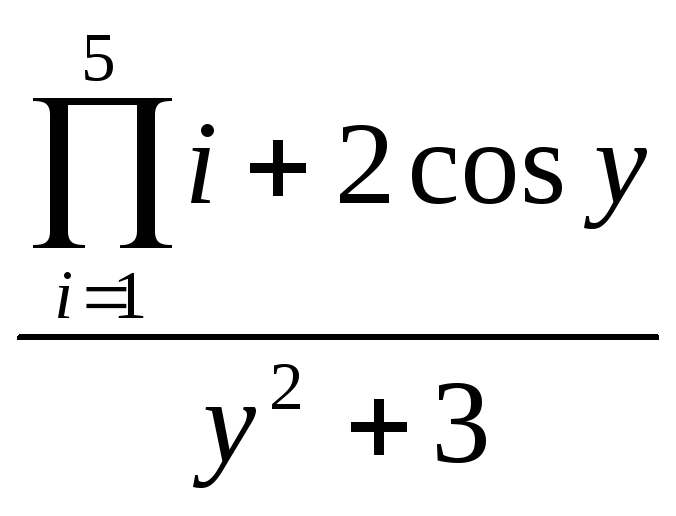
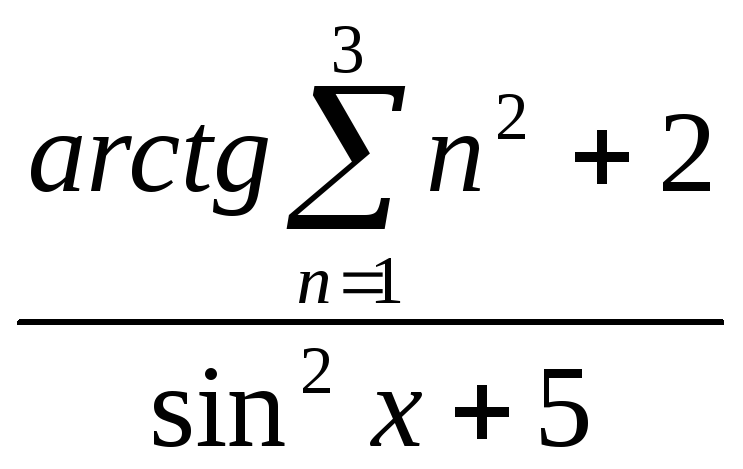
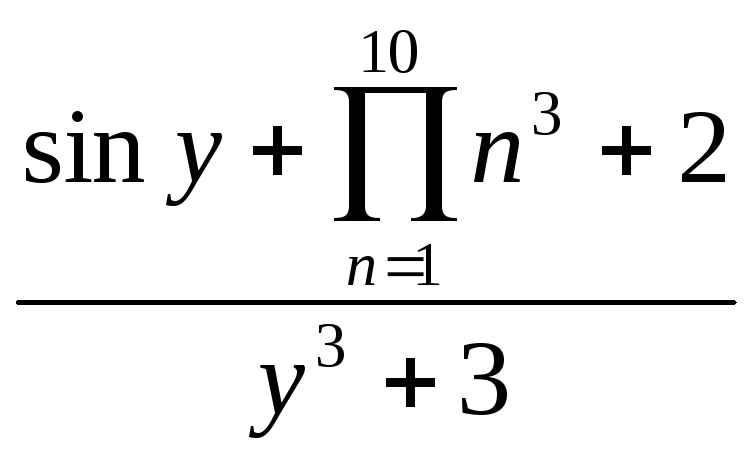
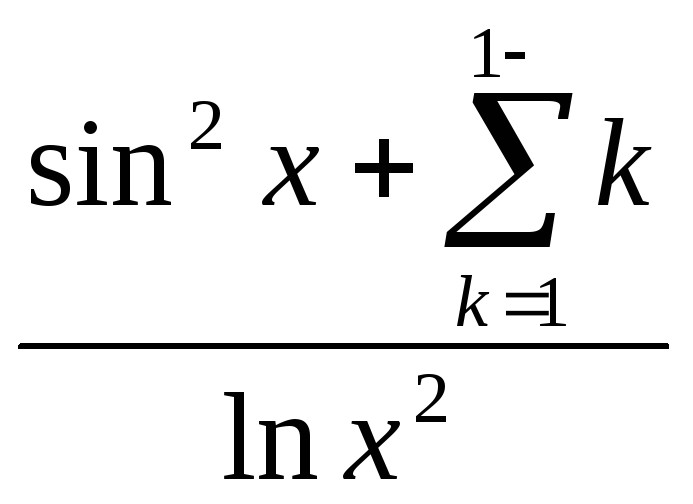
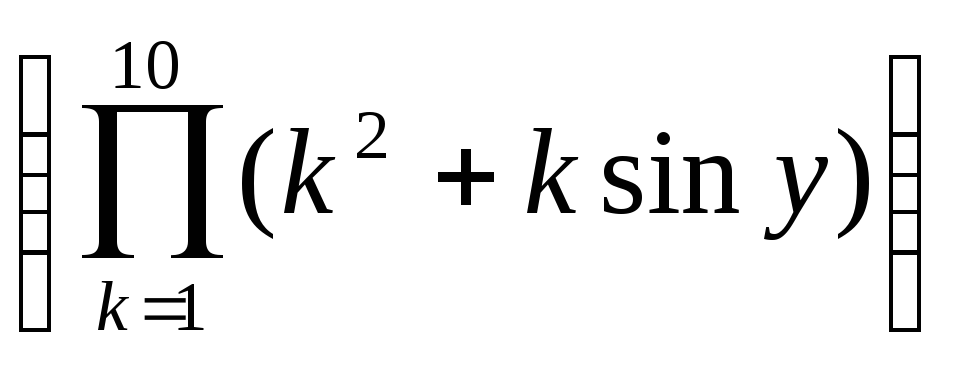
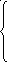 x2 +
x2 +
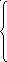
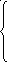 Siny+
Siny+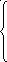 +
+
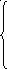 Sinx+
Sinx+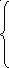 Cosx+
Cosx+
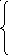 nx-
nx-
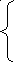 +
+
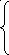 3
+
3
+
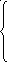 +lna, если
а < 3
+lna, если
а < 3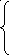 3+
3+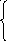 +
+
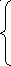 8
8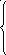 19
19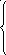 20
20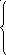 21
21 22
22 23
23 24
24 25
25 26
26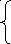 27
27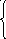 28
28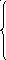 29
29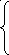 + 2sinx,
если x<2
+ 2sinx,
если x<2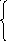 X3+ 3sin2x, если 1
X3+ 3sin2x, если 1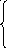
 Y3+ 2cosy,
если у < 3
Y3+ 2cosy,
если у < 3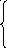 Arctg
Arctg
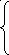 ln
ln