Лекция № 9

РАСЧЕТ ПРОЧНОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ

1. Расчет прочности нормальных сечений

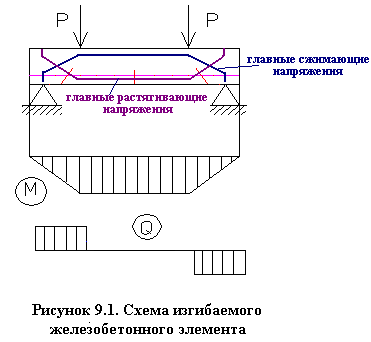
Рассмотрим для примера однопролетную железобетонную балку, свободно лежащую на двух опорах, симметрично загруженную двумя сосредоточенными силами. Участок балки между грузами находится в условиях чистого изгиба; в его пределах действует только изгибающий момент М, поперечная сила равна нулю. На определенной ступени загружения в бетоне растянутой зоны этого участка под воздействием растягивающих напряжений образуются нормальные трещины, т.е. трещины, направленные перпендикулярно продольной оси балки. На участках между опорой и грузом действует одновременно изгибающий момент М и поперечная сила Q. Здесь образуются наклонные трещины.

В сечениях, нормальных к продольной оси элементов, – изгибаемых, внецентренно сжатых, внецентренно растянутых – при двузначной эпюре напряжений в стадии III характерно одно и то же НДС. В расчетах прочности элементов усилия, воспринимаемые сечением, нормальным к продольной оси элемента, определяют по расчетным сопротивлениям материалов с учетом коэффициентов условий работы.

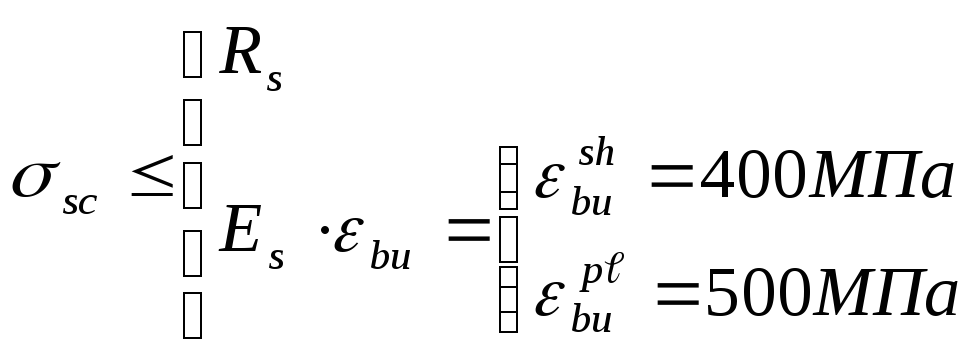
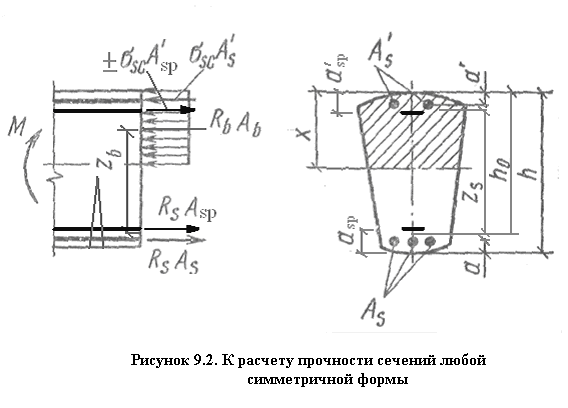
В общем случае условие прочности при любом из перечисленных внешних воздействий формулируется в виде требования о том, что момент внешних сил не превосходил момента внутренних усилий.

,

где М – в изгибаемых элементах – момент внешних сил от расчетных нагрузок; статический момент площади сечения бетона сжатой зоны относительно той же оси; расстояние между центром тяжести бетона сжатой зоны и центром тяжести растянутой (напрягаемой и ненапрягаемой) арматуры.

2. Общий случай расчета нормальных сечений

Основные предпосылки:

1. Растянутый бетон в работе сечения не учитывается;

2. Эпюра напряжений бетона в сжатой зоне принимается прямоугольной;

3. Сжатая зона ограничена линией, параллельной нейтральной оси (нейтральному слою), но не совпадающей с ней;

4. Рабочая высота сечения принимается для каждого арматурного слоя индивидуально;

5. Распределение напряжения в арматуре осуществляется с использованием гипотезы плоских сечений;

6. Соотношение между условной линией, ограничивающей сжатую зону, и фактическим нейтральным слоем учитывается коэффициентом полноты эпюры напряжений.

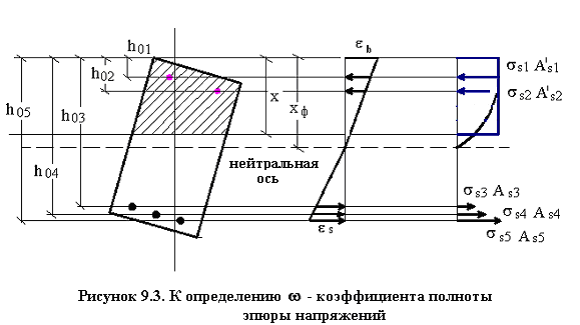
– определяется по формуле 26 СНиП 2.03.01-84*.

Высоту сжатой зоны для сечений, работающих по случаю 1, когда в растянутой арматуре и сжатом бетоне достигнуты предельные сопротивления, определяют из уравнения равновесия:

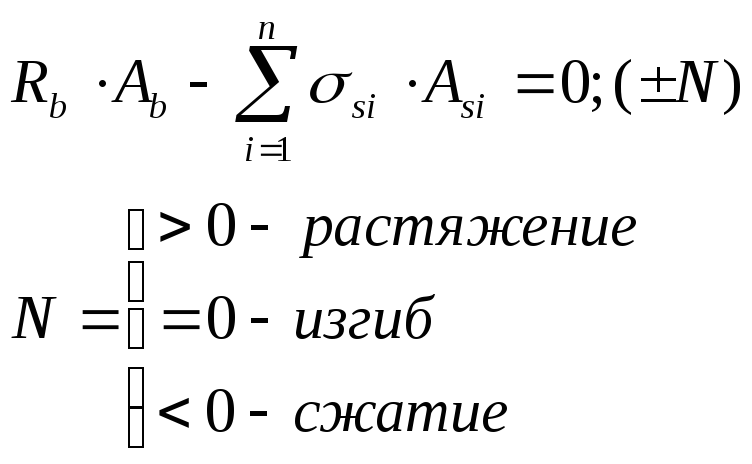
При изгибе уравнение моментов запишется как

где – статический момент.

Распределение напряжений по высоте сечений происходит линейно:

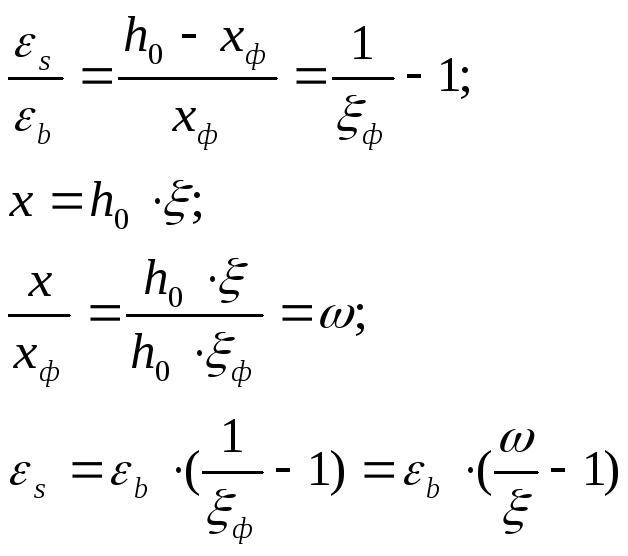
предельная деформация в бетоне сжатой зоны

,

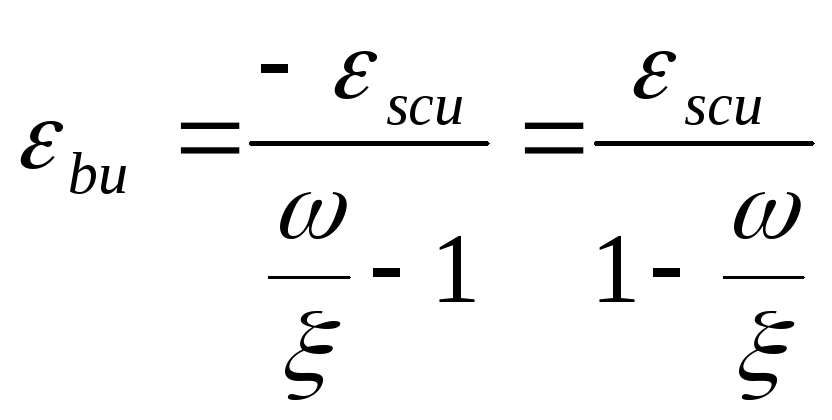где -предельная деформация в арматуре сжатой зоны.

При центральном сжатии принимают, что , тогда относительная высота сжатой зоны равна

тогд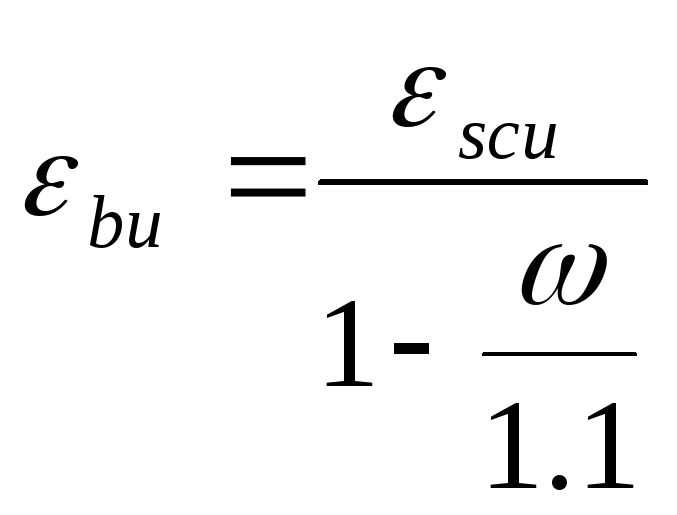а , а

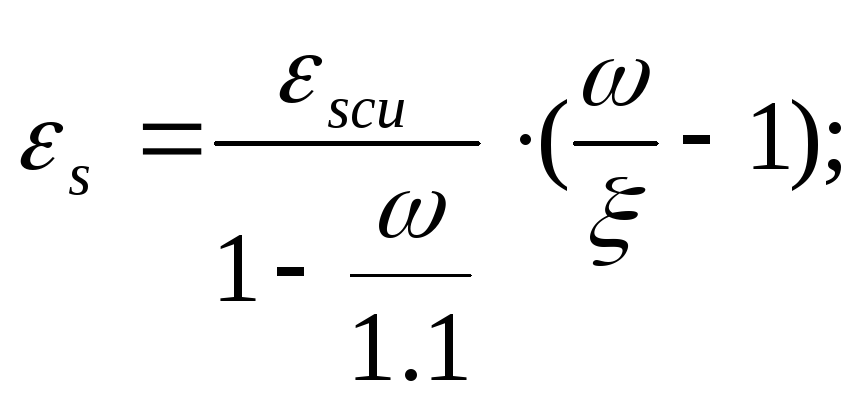
напряжение в i-ом стержне продольной арматуры:

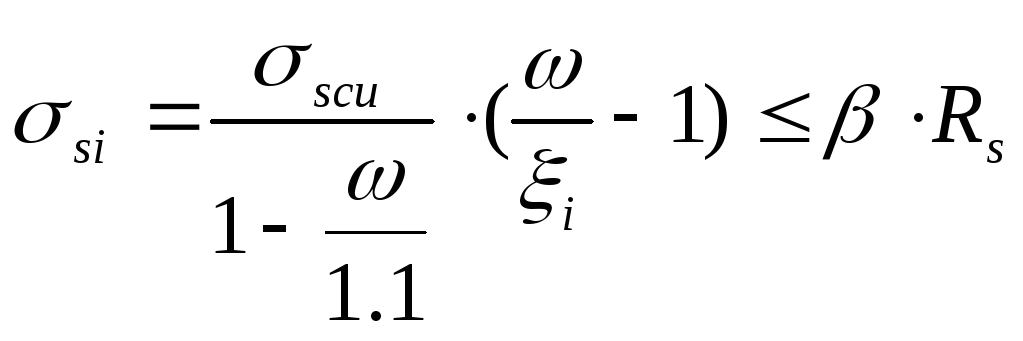, (1)

где предельное напряжение в арматуре сжатой зоны,

- коэффициент отношения сопротивления арматуры в упругой зоне к общему сопротивлению арматуры.

При механическом, а также автоматизированных электротермическом, электромеханическом способах предварительного напряжения арматуры классов A-IV, A-V, A-VI

,

где предварительное напряжение в i-ом стержне продольной арматуры, принимаемое при коэффициенте ,назначаемом в зависимости от расположения стержня.

Для арматуры классов B-II, Bp-II, K-7, K-19 при

Значение принимается при коэффициенте <1 c учетом потерь .

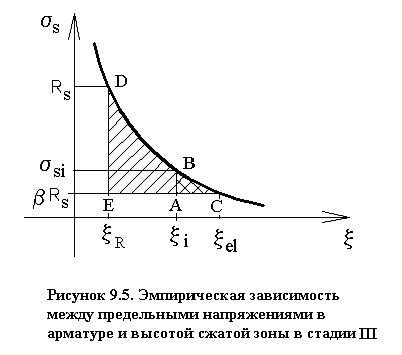
Из подобия треугольников ABC EDC:

(2)

Граничная высота сжатой зоны

Принимаем предположение, что . Тогда и уравнение (1) преобразуется:

,

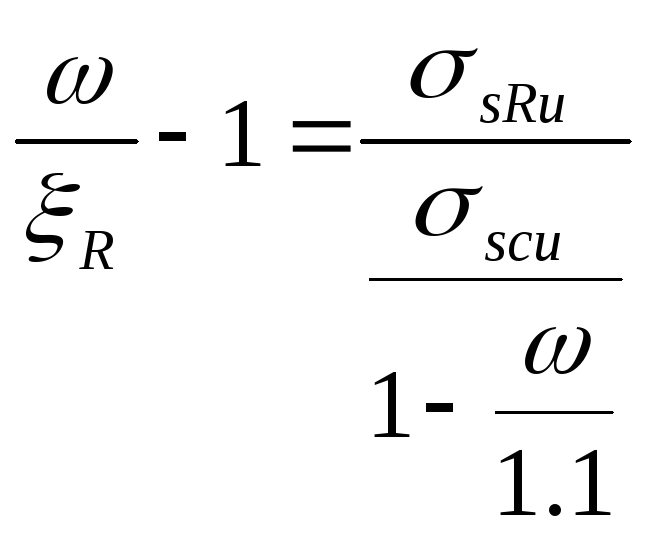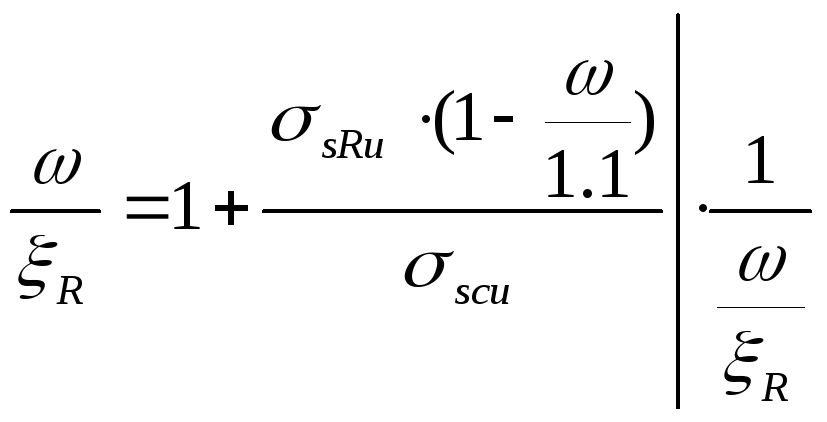
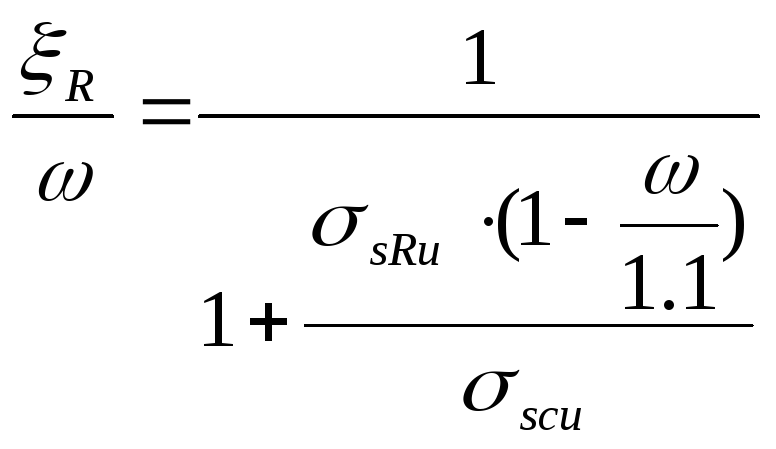
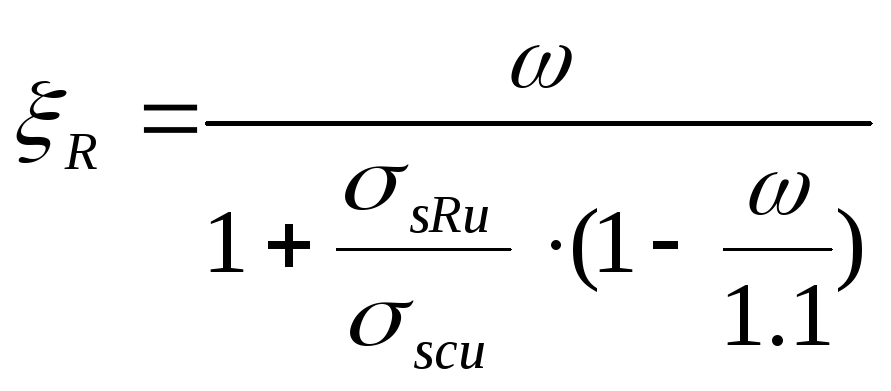
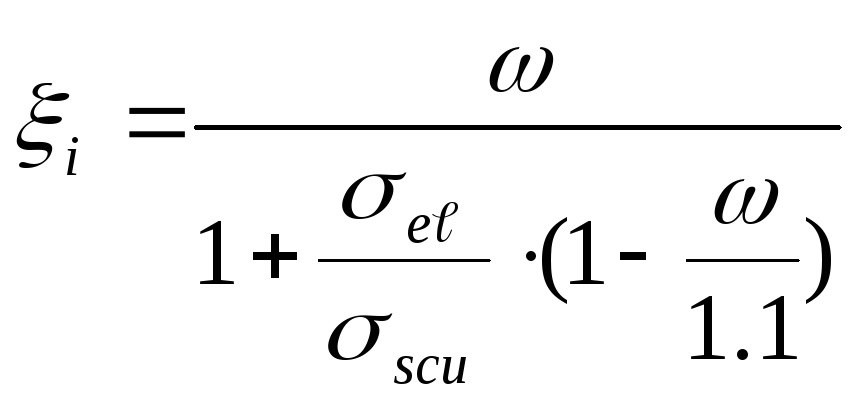
условное напряжение, которое при выполнении закона Гука соответствует граничной высоте сжатой зоны.

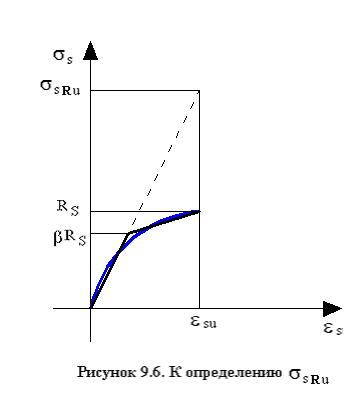
напряжение в арматуре, МПа, принимаемое для арматуры классов:

A-I, A-II, A-II, Bp-I

B-II, Bp-II, K-7, K-19

6