Лекция 12

ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ. РАСЧЕТ ПРОЧНОСТИ ПО НАКЛОННЫМ СЕЧЕНИЯМ

1. Основные расчетные положения

При изгибе железобетонного элемента возникают, кроме нормальных напряжений, скалывающие, действующие по горизонтальному и вертикальному направлениям.

В наклонных сечениях имеют место те же 3 стадии НДС, как и в нормальных сечениях.

После образования наклонной трещины изгибаемый элемент разделяется на части, соединенные бетоном сжатой зоны и арматурой, пересекающей наклонную трещину.

При увеличении нагрузки наклонная трещина раскрывается, и разрушение происходит по одному из трех возможных случаев.

Случай 1 – раздробление бетона стенки по наклонной полосе между наклонными трещинами от главных сжимающих напряжений.

Это обусловлено тем, что в стенке по взаимно перпендикулярным площадкам действуют сжимающие и растягивающие напряжения. Последние существенно снижают прочность на сжатие.

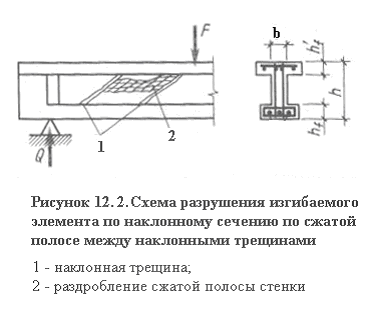
Случай 2 – сдвиг по наклонному сечению от доминирующего действия поперечной силы.

Образование наклонной трещины начинается в середине боковых граней, где касательные напряжения достигают своего максимального значения.

Если касательные напряжения не достигают своего максимального значения, то наклонной трещины не образуется.

Случай 3 – излом по наклонному сечению от доминирующего действия изгибающего момента М.

Это обусловлено тем, что главные растягивающие напряжения преодолевают сопротивление бетона на осевое растяжение. Наклонная трещина образуется с максимальным раскрытием в растянутой зоне. Бетон растянутой зоны в наклонном сечении выключается из работы, и все растягивающие усилия передаются арматуру. Происходит взаимный поворот частей элемента вокруг мгновенного центра вращения. Арматура течет или при слабом заанкерении выдергивается даже при небольших значениях изгибающего момента, сжатая зона сокращается и разрушается. При наличии сильной заанкеренной продольной арматуры в результате совместного действия срезающих и сжимающих усилий разрушается бетон сжатой зоны.

Если главные растягивающие напряжения не достигают значения осевого сжатия, то наклонной трещины не образуется и поперечная сила полностью воспринимается одним бетонным сечением.

Прочность элементов по наклонным сечениям на совместное действие изгибающего момента М и поперечной силы Q рассчитывают в зависимости от случая разрушения элементов.

Исходя из описанной схемы излома элемента, разрушающий момент и разрушающая поперечная сила в наклонном сечении равны:

–сумма проекций внутренних усилий на нормаль к оси элемента.

– сумма моментов внутренних усилий относительно точки приложения равнодействующей сжатой зоны на нормаль к оси элемента.

площадь сечения соответственно поперечной арматуры (хомутов), наклонной арматуры (отгибов), продольной (рабочей) арматуры;

расстояние до точки D соответственно от хомутов, отгибов и продольной арматуры.

2. Определение положения расчетного наклонного сечения

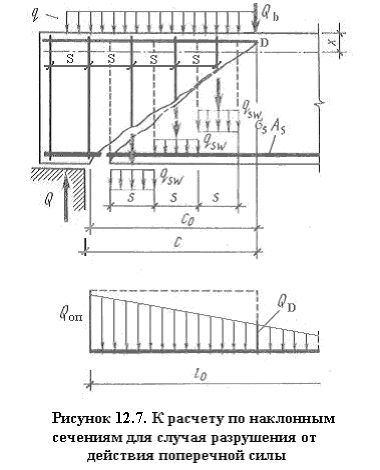
Рассмотрим общий случай армирования изгибаемого элемента одновременно поперечными и наклонными стержнями, размещенными равномерно и достаточно часто.

Из всех возможных наклонных сечений, проходящих через начало наклонной трещины, необходимо найти наклонное сечение минимальной прочности – положение опасного наклонного сечения, которое и будет расчетным.

Q_D – поперечная сила над трещиной;

Q – поперечная сила, определяемая от внешней нагрузки;

Q_sw – сумма усилий в поперечных арматурных стержнях, пересекаемых опасным наклонным сечением;

Q_s.inc – сумма проекций на нормаль к продольному направлению балки усилий, пересеченных опасным наклонным сечением;

Q_b – поперечное усилие, воспринимаемое бетоном;

q – внешняя равномерно распределенная нагрузка, действующая по граням балки;

с – длина проекции опасного наклонного сечения на продольную ось элемента;

c₀ – длина проекции опасной наклонной трещины на продольную ось элемента.

Прочность элемента в наклонном сечении достаточна, если поперечная сила Q в наклонном сечении от расчетных нагрузок не превосходит суммы проекций на нормаль к оси элемента внутренних расчетных усилий в стержнях арматуры, пересекаемых наклонным сечением, и в бетоне сжатой зоны. С учетом того, что :

Очевидно, что расчетным наклонным сечением будет такое, в котором несущая способность имеет наименьшее значение.

3. Расчет по наклонным сечениям для случая разрушения между наклонными трещинами

Расчет производится от действия главных сжимающих напряжений:

где – наибольшее значение поперечной силы от внешней нагрузки (опорная реакция);

– коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента:

;

площадь сечения хомутов, расположенных в одной нормальной к оси элемента плоскости;

s – шаг хомутов;

коэффициент, зависящий от характеристик бетона:

,

где 0,01 – для тяжелого, мелкозернистого и ячеистого бетона;

0,02 –для легкого бетона.

принимается в МПа с учетом коэффициента .

 

  

4. Расчет по наклонным сечениям для случая разрушения от действия поперечной силы

В реальных конструкциях нагрузка q в пределах наклонной трещины может отсутствовать. Поэтому нормы предписывают учитывать уменьшение поперечной силы за счет нагрузки q, расположенной в пределах наклонного сечения лишь в тех случаях, когда нагрузка q является безусловно действующей (например, давление грунта или воды).

Технологически отгибы устанавливать сложно, поэтому их применяют крайне редко. Таким образом, расчет наклонных сечений рассмотрим при условии, что .

Исходя из выше написанного, получаем:

По СНиП 2.03.01-84* поперечное усилие, воспринимаемое бетоном, равно

,

где коэффициент, учитывающий тип бетона (для тяжелого бетона );

коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах, т.е. свесы:

;

;

коэффициент, учитывающий влияние продольных сил.

При этом должно соблюдаться условие, что .

Таким образом, можно записать следующее:

Поперечное усилие в хомутах определяют как:

,

количество поперечных стержней, которые пересекает опасная наклонная трещина в опасном наклонном сечении.

Но так как величина дискретная, а непрерывная функция, то в расчетах используют интенсивность .

Таким образом, получаем

При действии усилий на проекции наклонной трещины с:

Тогда

()

Длина проекции расчетного опасного сечения устанавливается из условия:

тогда

Тогда проекция наклонного сечения, опасного по несущей способности:

, т.е.

Рассмотрим случай, когда . Тогда формула () преобразуется в следующее выражение:

,

т.е.

– несущая способность наклонного сечения