
НУ
.pdf
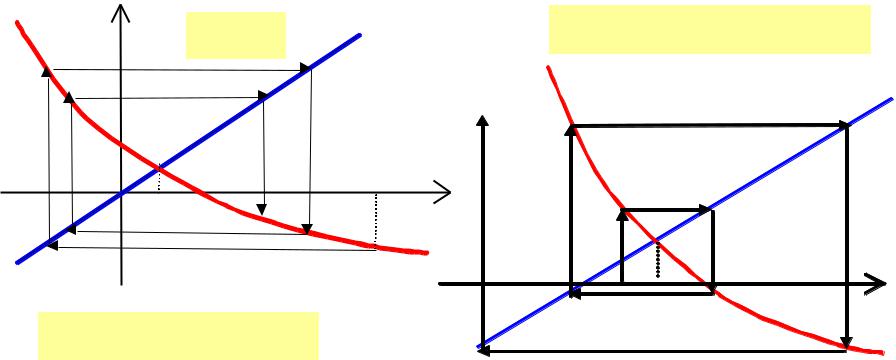
Метод простых итераций
ВСЕГДА ЛИ МЕТОД СХОДИТСЯ ?
y |
y=(x) |
|
y=x |
|
|
x0) |
|
метод расходится ! |
x1) |
x |
y |
|
||
x* x2 x1 |
x0 |
y= (x) |
|
||
|
|
y=x |
x
метод сходится |
x0 x* |
x1
x2
ЧЕМ ОТЛИЧАЮТСЯ ЭТИ ДВЕ ФУНКЦИИ ?
Метод простых итераций
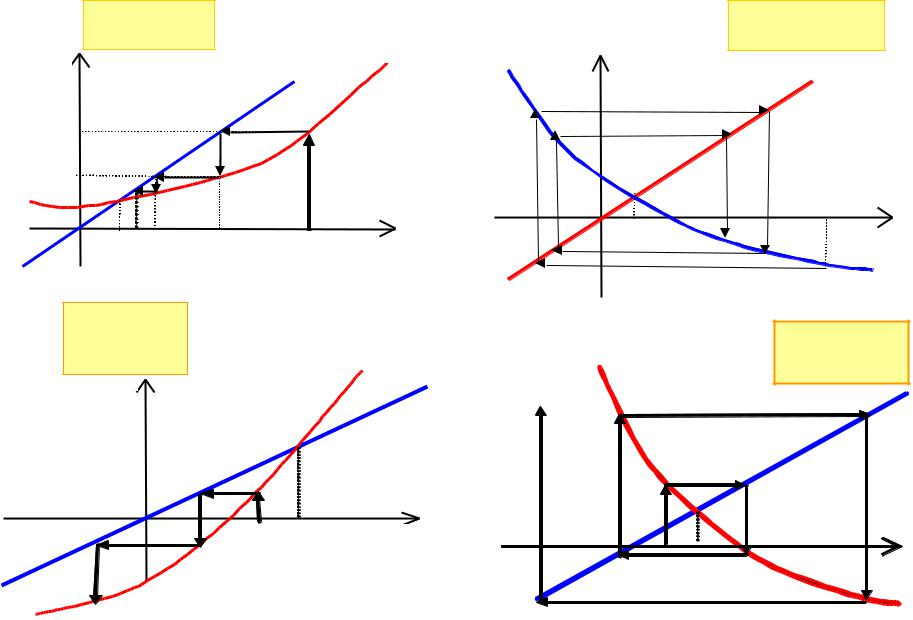
ВСЕГДА ЛИ МЕТОД СХОДИТСЯ ?
y |
< 0 |
метод расходится |
|
y y= (x)
y= (x)
x1 x3 |
x4 x2 x0 |
x |
x1 |
x |
2 |
|
3 |
|
x4 |
x0 |
метод сходится |
|
|
|
|
ЧЕМ ОТЛИЧАЮТСЯ ЭТИ ДВЕ ФУНКЦИИ ?
Геометрический смысл метода простой итерации
0 / |
1 |
Сходящийся метод простой итерации 1 / 0 |
||||||
y |
|
|
y=(x) |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=x |
|
|
|
|
|
|
x0) |
|
|
|
|
|
y= (x) |
|
|
x1) |
|
|
|
|
|
|
|
|
|
|
x |
x1 |
x3 |
|
x4 x2 |
x0 |
|
|
|
|
|
|||||
|
|
|
|
|
||||
x* x2 |
x1 |
x0 |
|
|
|
|
|
|
/ |
1 |
Расходящийся метод простой итерации / |
1 |
|||||
|
y |
|
|
y |
|
y= (x) |
|
|
|
|
|
y= (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x0 x* |
|
x |
2 |
x1 |
x |
|
|
|
|
|
|
3 |
||
|
|
x1 |
|
x4 |
|
x0 |
|
|
|
|
|
|
|
|
|
||
x2

Метод простых итераций
xk+1= (xk)
Необходимое условие сходимости: | (x*) | < 1
Достаточное условие сходимости:
| (x) | < 1, x [a,b]

Метод простых итераций
Решить уравнение f(x)= x2 - 4x |
+ 3=0, |
[a,b]= |
||||
с точностью =0.001 |
|
|
|
|
|
|
Преобразуем исходное уравнение к виду: |
x |
|||||
|
(x) |
x2 |
3 |
|
||
Проверка условия |
|
4 |
|
'(0) 0 |
|
|
|
|
|
|
|||
|
|
|
|
|
||
'(x) x / 2 |
|
|
||||
сходимости |
|
|
||||
|
|
|
|
'(1.5) 0.75 |
||
|
|
|
|
|
|
|
[0, 1.5],
x2 3
4

 '(x) 1
'(x) 1
k |
xk |
xk+1 |
|xk+1-xk| |
|
|
|
|
0 |
0 |
0,75 |
0,75 |
|
|
|
|
1 |
0,75 |
0,890625 |
0,140625 |
|
|
|
|
2 |
0,890625 |
0,948303 |
0,057678223 |
|
|
|
|
3 |
0,948303 |
0,97482 |
0,026516528 |
|
|
|
|
4 |
0,97482 |
0,987568 |
0,012748636 |
|
|
|
|
5 |
0,987568 |
0,993823 |
0,006254443 |
|
|
|
|

Метод релаксации
Универсальный вариант МПИ: xk+1= (xk)
Выбор функции (x) в виде : (x) = x –с f (x)
/ (x) 1 cf / (x) 1, 1 1 cf / (x) 1, 2 cf (x) 0,
Параметр релаксации с 0 подбирается таким образом,
чтобы выполнялось. достаточное условие сходимости метода: (x) <1
Если f (x) < 0, то
Если f (x) > 0, то
2
f(x)
2
f (x)
С 0
С 0
Знак С совпадает со знаком f’(x)
Метод релаксации
Параметр релаксации С можно выбирать в виде:
c 2 /(M m), где M max( f / (x)), m min( f / (x))
В качестве начального. приближения обычно берут середину интервала изоляции [a,b]:
x0 (a b) / 2

Пример
Решить методом |
x3 |
3x2 |
3 0 |
|
релаксации уравнение: |
||||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
f(x) |
|
|
|
|
|
1 |
|
|
|
|
|
3 2 |
|
|
|
|
|
3 |
2 |
1 |
|
|
|
3 |
0 |
1 |
2 |
||
3 |
|
|
x |
|
2 |
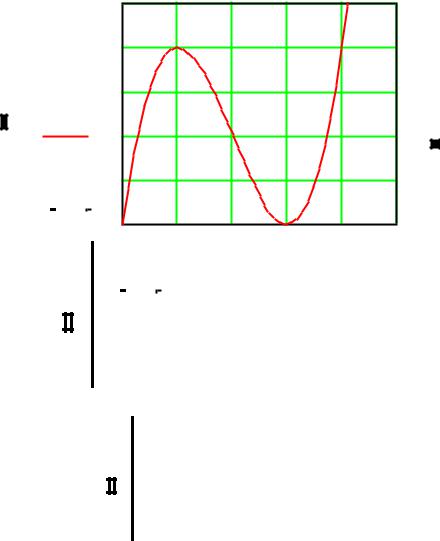
Определяем интервалы изоляции:
[-3, -2] [-2. -1], [0, 1]

Программа метода релаксации
Процедура-функция для решения уравнения f(x)=0
relax(x c ) |
|
k 0 |
|
|||
|
|
|||||
|
|
(x) x c f (x) |
||||
|
|
|
|
|||
|
|
while |
x (x) |
|||
|
|
|
|
x (x) |
|
|
|
|
|
|
|
||
|
|
|
|
k k 1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
k |
|
|||
|
|
|
||||
|
|
|
||||
|
|
|
|
|||
|
|
x |
|
|||
Вызов П-Ф метода релаксации
Первый корень: |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция возрастает, С>0 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
relax( 2 0.2 0.001) |
|
|
6 |
|
0 |
|
|
|
|
|
2.532 |
f(x) |
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Второй корень: |
|
|
|
|
3 2 |
|
|
|
|
|
функция убывает, С<0 |
|
|
3 |
2 |
1 |
0 |
1 |
2 |
||
|
|
|
|
|
3 |
|||||
|
|
9 |
|
3 |
x |
2 |
relax(0 0.2 0.001) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
1.346 |
|
|
|
|
Третий корень: функция возрастает, С>0 |
|
|
||||
|
|
10 |
|
relax(0 0.2 0.001) |
|
|
|
|
|||
|
|
0.88 |
|
