
НУ
.pdfРешение нелинейных алгебраических уравнений
II курс, 2 семестр, 2014
ПОСТАНОВКА ЗАДАЧИ
Дано нелинейное алгебраическое уравнение F(x)=0
Решить уравнение: найти такое x* R: F(x*)=0.
Значение x* называют корнем уравнения.
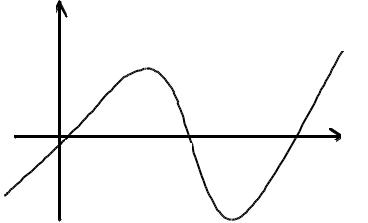
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
y |
y=F(x) |
x1* |
x * |
x3* x |
|
2 |
|
Корнями уравнения являются точки x1*, x2*, x3*, в которых функция F(x) пересекает ось x.
УСЛОВИЕ СУЩЕСТВОВАНИЯ КОРНЯ
на отрезке [a,b]
ЕСЛИ: F(x) непрерывна, F(a) F(b)<0 (т.е. на концах интервала функция имеет разные знаки).
ТОГДА: внутри отрезка [a, b] существует хотя бы один корень уравнения F(x)=0.
Условие единственности корня на отрезке [a,b]:
•Корень будет единственным, если F (x) не меняет знак на отрезке [a, b] (т.е. F(x) – монотонная функция)
•Отрезок [a,b], на котором существует единственный корень уравнения - интервал изоляции
МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЯ
•точные (аналитические) → конечное число действий
•приближенные (итерационные) → процесс нахождения решения бесконечен
Приближенным решением называется бесконечная последовательность {xn}, такая, что
lim xn x*
n
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
ПОСЛЕДОВАТЕЛЬНОСТЬ: |
lim xn x* |
|
|
|
n |
Предел: (сколь угодно малого), найдется такое N, что при n > N, |xn – x*|< .
xn - последовательные приближения, или итерации.
Заданное малое число - точность метода,
N – количество итераций, которое необходимо выполнить, чтобы получить решение с точностью .
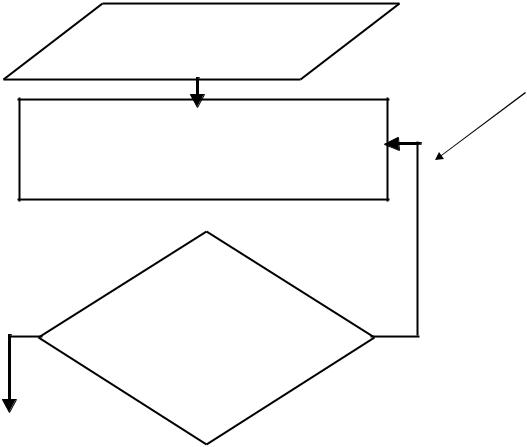
ОБЩИЕ ЭТАПЫ
РЕШЕНИЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ
Задать начальное приближение x0
Найти следующее приближение
xn+1= (xn, xn—1, …, x1, x0)
 Не Выполвыполнено нено
Не Выполвыполнено нено
Условие
точности
решения
Итерационный цикл
ПРОВЕРКА ТОЧНОСТИ РЕШЕНИЯ:
1.|xn–x*|<
2.F(xn) <
3.|xn+1–xn|<
Прежде, чем решать уравнение приближенно, его надо исследовать, т.е. найти количество корней и их расположение (начальное приближение)
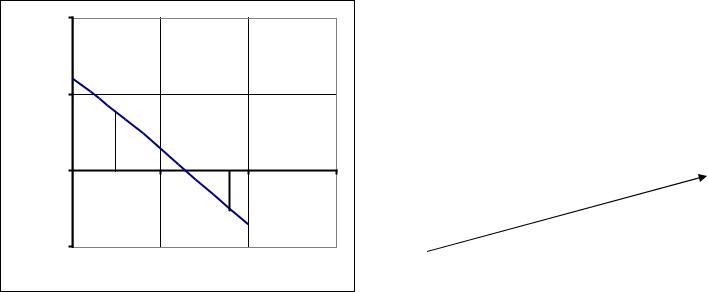
СПОСОБЫ ИССЛЕДОВАНИЯ ФУНКЦИИ:
• АНАЛИТИЧЕСКИЙ: |
|
|||
поиск экстремумов функции F(x), участков |
||||
возрастания и убывания, поведение на |
||||
•ГРАФИЧЕСКИЙ: |
|
|||
построение графика функции F(x) и |
||||
определение интервалов, на которых F(x) |
||||
меняет знак |
|
|
||
1 |
|
|
|
|
y |
|
|
|
|
0.5 |
|
F(a) |
|
|
|
|
|
|
|
0 |
|
x* |
b |
x |
|
|
|
|
|
2.5 |
a |
3 |
3.5 |
4 |
|
|
|
|
|
|
|
F(b) |
|
|
-0.5 |
|
|
|
|
•ТАБЛИЧНЫЙ : построение таблицы x, F(x) и |
||||
определение интервалов смены знака F(x) |
||||
x |
F(x) |
-10 |
-1619 |
-9 |
-1231 |
-8 |
-909 |
-7 |
-647 |
-6 |
-439 |
-5 |
-279 |
-4 |
-161 |
-3 |
-79 |
-2 |
-27 |
-1 |
1 |
0 |
11 |
1 |
9 |
2 |
1 |
3 |
-7 |
4 |
-9 |
5 |
1 |
6 |
29 |
7 |
81 |
8 |
163 |
9 |
281 |
10 |
441 |
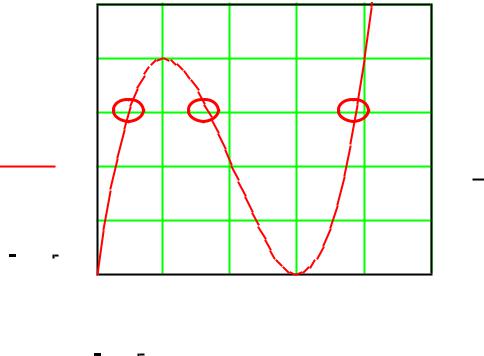
Графический метод отделение корней нелинейного уравнения
Построим график функции и найдем интервалы изоляции
ПРИМЕР 1: Дано алгебраическое уравнение
2 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
f(x) |
|
|
|
|
|
1 |
|
|
|
|
|
3 2 |
|
|
|
|
|
3 |
2 |
1 |
|
|
|
3 |
0 |
1 |
2 |
||
3 |
|
|
x |
|
2 |
x3 3x2 3 0
Интервалы изоляции:

 [-3, -2] [-2. -1], [0, 1]
[-3, -2] [-2. -1], [0, 1]
Уточнение корней
Использовать функцию MathCAD root,
Функция root может иметь два или четыре аргумента:
root( f (x), x) root( f (x), x, a,b)
f(x) – имя функции, задающей уравнение,
x–переменная, относительно которой решается уравнение
a, b – границы интервала локализации корня
Можно искать и вещественные, и мнимые корни
С помощью функции root найти все корни из ПРИМЕРА 1

Пример 2 (начало)
Дано алгебраическое уравнение x3 6x2 21x 52 0
Строим график функции
f(x)=x3-6x2+21x+52
Уравнение должно иметь 3 корня
Один корень вещественный, интервал изоляции [-2, 0]
Два корня комплексные
