
Оптика. Строение атома. Атомное ядро
.docx|
1.Элементы геометрической оптики: законы прямолинейного распространения света, отражения и преломления. Коэффициент преломления. Закон прямолинейного распространения света Опытным доказательством этого закона в однородной оптической среде могут служить наблюдения над резкими тенями, создаваемыми точечными источниками света или получение изображений при помощи малых отверстий (камера обскура). Форма тени на экране соответствует форме геометрической проекции , полученной при проецировании прямых линий, исходящих из источника света. Аналогичен способ получения изображений с помощью малых отверстий Закон независимости световых пучков. В обычных условиях лучи, исходящие от различных объектов, многократно пересекаются. Эти пересечения никоим образом не мешают каждому из лучей распространяться независимо друг от друга, т.е. эффект производимый одним лучом не зависит от того действуют ли одновременно другие лучи или нет. Закон отражения света. Отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;угол отражения равен углу падения. Закон преломления света. Луч падающий и луч преломленный лежат водной плоскости с нормалью к границе раздела двух оптических сред Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:
|
2. Интерференция света. Когерентные источники света и когерентные волны. Оптическая длина пути, оптическая разность хода. Условия усиления и ослабления света при интерференции. В области перекрытия световых волн, которую называют полем интерференции, при выполнении определенных условий, можно наблюдать, что в одних местах волны, накладываясь, усиливают друг друга ,образуя максимумы интенсивности света, а в других ослабляют, образуя минимумы интенсивности. Эти условия максимума и минимума выражаются через соотношения между разностью оптических длин пути от двух источников до точки наблюдения и параметром, связанным с длиной волны источника. При этом под оптической длиной пути принимается величина, показывающая расстояние, которое пройдет луч света в вакууме за время его перемещения в оптической среде и равное произведению геометрического пути на абсолютный показатель преломления той среды , в которой идет луч света Волновые свойства света особенно отчетливо наблюдаются в явлении интерференции света. Для объяснения световых явлений в этом явлении достаточно рассматриваемые световые волны характеризовать их амплитудой, фазой , длиной волны, скоростью распространения и при этом не учитывать тот факт, что колебания в световой волне есть колебания векторов электрической и магнитной напряженностей, происходящих во взаимно перпендикулярных плоскостях. Наблюдения показывают, что для световых волн, так же как и для механических, соблюдается принцип суперпозиции. Условие максимума интерференции: ΔL=k*λ Условие
минимума интерференции: ΔL=(2k+1) Условие когерентности предполагает выполнение следующих условий:
Источником когерентных волн служат два точечных источника полученных от монохроматического действительного источника света 5 путем отражения света от двух плоских зеркал, расположенных под углом близким к 180° |
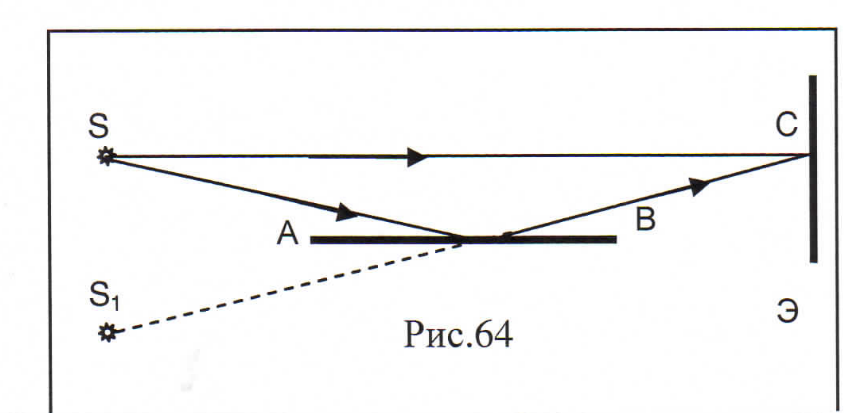
3. Способы наблюдения интерференции света (зеркала Френеля; бипризма Френеля; зеркало Ллойда). 1 2Бипризма Френеля Если свет от источника S пропустить через две призмы с малыми углами при вершине и сложенными основаниями, то обе призмы отклоняют лучи к основаниям и таким образом образуют два мнимых источника S(1) S (2) создадут, налагаясь, в точке D или другой точке интерференционную картину. 1 БизеркалаФринеля Источником когерентных волн служат два точечных источника S1 и S2, полученных от монохроматического действительного источника света S путем отражения света от двух плоских зеркал ОА2 и ОА2, расположенных под углом близким к 180°. Для нахождения расположения мнимых источников, находящихся за зеркалами, из точки S проводят окружность радиусом ОS и из т.Sпроводят расположения мнимых источников, находящихся за зеркалами, из точки 5 проводят окружность радиусом ОS и из т.S проводят перпендикуляры на зеркала до пересечения с окружностью. Полученные точки S1 и S2 являются мнимыми когерентными источниками и на экране Э в некоторой точке С получим либо светлую (темную) полоску в зависимости от разности хода лучей СS2- СS1 от мнимых источников. В целом на экране получим чередование светлых и темных полос (если источник 5 имеет вид щели параллельной ребру сочленения зеркал (т О). 3 Зеркало Ллойда В опыте Ллойда в некоторой точке экрана С интерферируют два луча - один непосредственно от источника S, а второй отраженный от поверхности зеркала АВ. Источником света служит щель параллельная зеркалу, причем источник S расположен очень близко к зеркалу. Тогда мнимый источник S' оказывается близко к S и на экране образуется система из чередующихся светлых и темных полос.
|
|
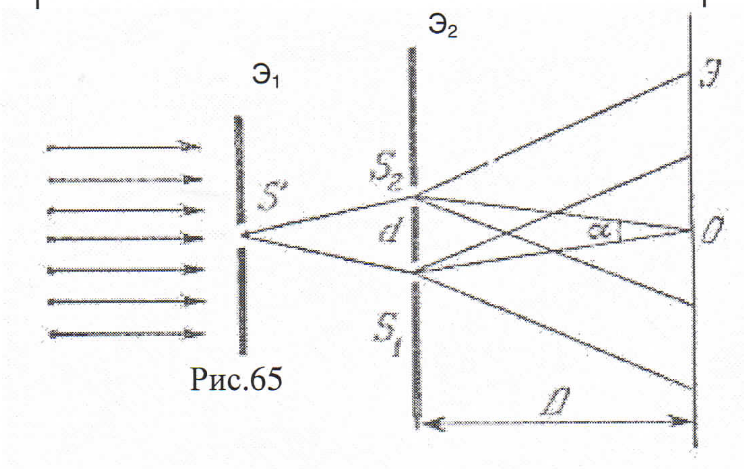
4. Опыт Юнга. Минимум и максимум положения интерференции на экране. Один из классических опытов по интерференции - опыт Юнга В экране Э1 сделано отверстие малой ширины в виде щели. Если на него падает монохроматический свет, то согласно принципа Гюйгенса это отверстие будет источником полусферических волн, которые достигая экрана Э2 с двумя малыми отверстиями, создают два источника S (1) и S (2) , испускающие волны в одной фазе и одинаковой амплитудой, т.е. когерентные источники. Если в поле интерференции поместить непрозрачный экран Э , то будет наблюдается чередование светлых и тёмных полос представляющие собой интерференционную картину. Параметрами интерференционной картины являются положение её максимумов (светлые полоски) хmax и минимумов (темные полоски) хmin относительно центральной точки О расположенной симметрично по отношению к щелям, а также связанная с ними ширина полос интерференционной картины, т.е. расстояние между двумя минимумами. Положение светлой полосы на экране (максимум) по отношению к т. О
Если перемещать экран, то в т..О будет то максимуму (свет), то минимум (тень), т.к. будет меняться число зон Френеля. Если пользоваться белым светом, представляющий набор монохроматических длин волн, то положение минимумов и максимумов для разных волн различно и, скажем найдется такое место, где полоса красного света наложится на полосу синего света (и других цветов) и интерференционной картины не будет. |
||
|
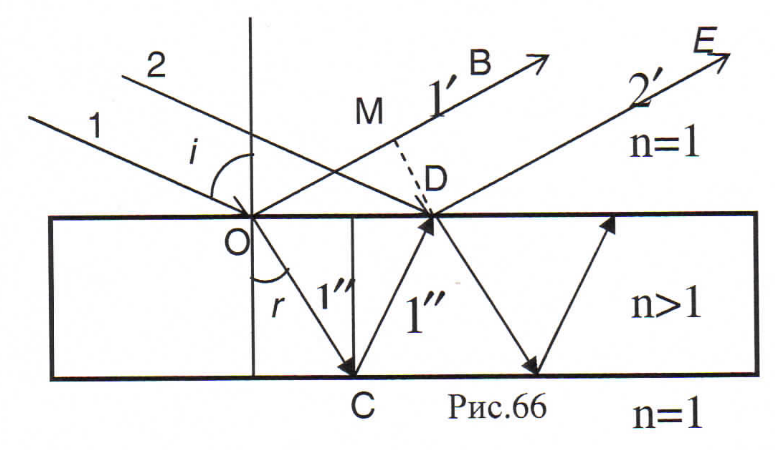
5. Интерференция в тонких пленках и пластинках (полосы равного наклона). Как идут лучи, где локализация картины? Резкие интерференционные максимумы и минимумы будут иметь место в случае точечных и монохроматических источников света. Тогда помещая экран в любое место около источников можно получить интерференционную картину и т .о. она не локализована в одном месте. Однако нам чаще всего приходится использовать протяженные источники света с набором длин волн. Интерференция в этом случае может наблюдаться при освещении тонких прозрачных пластинок , когда необходимое для возникновения когерентных пучков света возникает вследствие эффекта расщепления световой волны вследствие отражения света от поверхностей пленки или пластинки. В тоже время оптический путь луча прошедшего путь в пленке до т. В будет равен (OC+CD)*n ,а луч 1 отразившись в т. О пройдет до т. М путь равный ОМ. Кроме того, если луч 1’’отражается в т. С от менее плотной среды(воздуха), то отраженный в т. О луч от плотной среды – пленки и в результате у него изменится фаза на противоположную, что соответствует потере полуволны. Таким образом между лучами 1' и 2' возникнет разность хода. ΔL= В результате преобразований получаем оптическую разность хода ΔL=2d
|
||
|
|
||
|
|
6. Интерференция полос равной толщины. Как идут лучи, где локализация картины? Достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Возникающие при этих условиях полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п. Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина). Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают. Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость). Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности. Результат
интерференции в точках P1
и P2
экрана определяется по известной
формуле
Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис. 8.11). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
|
|
|
7. Кольца Ньютона (рисунок, радиусы колец). Кольца
Ньютона —
кольцеобразные интерференционные
максимумы и минимумы, появляющиеся
вокруг точки касания слегка изогнутой
выпуклой линзы и плоскопараллельной
пластины при прохождении света сквозь
линзу и пластину. Δ=(2m+1) Радиус
k-го
светлого кольца Ньютона (в предположении
постоянного радиуса кривизны линзы)
в отражённом свете выражается следующей
формулой: k = 2, 4, …;λ — длина волны света в вакууме;n — показатель преломления среды между линзой и пластинкой.
|
8. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля. Дифракция света, как и интерференция, является доказательством волновой природы света. В основе Дифракции лежит принцип, помогающий сделать приближенный расчет дифракционных картин, в которых наблюдаются максимумы и минимумы интенсивности света. Принцип Гюйгенса приводит к выводу, что если фронт световой волны частично закрыт каким-нибудь экраном с отверстием, то световые волны будут огибать края этого отверсти . Явление огибания световыми волнами встречающихся препятствий и называют дифракцией света. Принцип Гюйгенса не позволяет найти интенсивность световых волн, распространяющихся при дифракции в различных направлениях. Френель предложил приближенный метод решения задачи о распространении волн, основанный на более глубоком представлении о волновом процессе, с учетом амплитуд и фаз колебаний. Сам принцип Гюйгенса-Френеля может быть сформулирован таким образом: каждую точку среды, до которой дошел волновой фронт, можно не только рассматривать как источник вторичных когерентных волн, но и волновое возмущение во всякой точке, находящейся перед фронтом волны, можно рассматривать как результат интерференции этих вторичных волн |
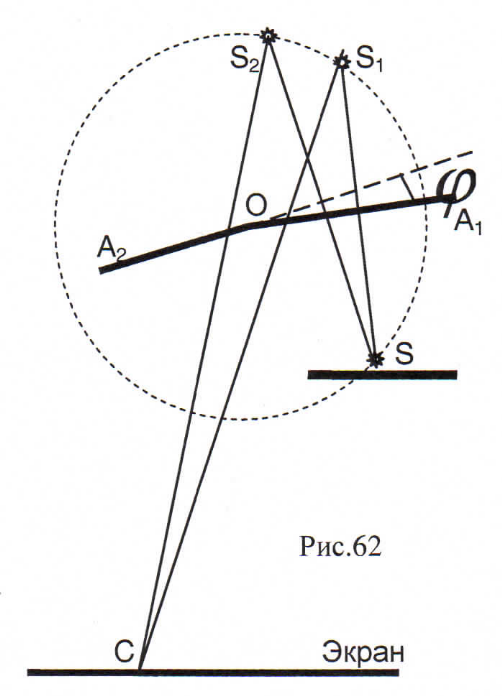
9. Метод зон Френеля. Доказательство прямолинейности распространения света. Если свет распространяется в виде вторичных световых волн от множества источников dS , лежащих на поверхности фронта световой волны, то почему мы не наблюдаем этих источников, а воспринимаем свет в виде узкого пучка, идущего от источника S? Как объяснить прямолинейность распространения света на основании волновой теории? Дифракция Френеля - это дифракция в сходящихся лучах, когда дифракционная картина наблюдается на конечном расстоянии от источника света, Для объяснения прямолинейности света Френель применил следующий метод. Рассмотрим точеный источник света S и сферический фронт АОС(рис. 72), находящийся на некотором расстоянии О- от источника. Френель заменил действие источника S на точку В, действием вторичных источников, расположенных на поверхности фронта. Площади этих источников получаются путем разбиения поверхности фронта сферами, которые проводятся из точки В (ОВ=b) и
радиусы увеличиваются на
Т.к. длина волны мала, то и радиусы будут отличаться очень мало друг от друга. Сферы вырежут на волновой поверхности ряд сферических сегментов, которые называют зонами. Центральная зона имеет вид шарового сегмента, а все остальные - вид кольцевых поясов.
|
|
10. Дифракционная картина от малого круглого отверстия, диска. Пусть волна, идущая от источника света, встречает на пути экран с круглым отверстием МN (рис. 73). Исследуем явление в т. А, лежащей на линии, соединяющей ее с центром отверстия. Из всего волнового фронта, падающего на экран, незакрытым останется участок в отверстии и результат действия этого участка в т. А будет зависеть от количества малых площадей вторичных волн (зон), которые могут уложиться в этом отверстии. Для нахождения этих площадей из на т. А проводим концентрические сферы, первая из которых проходит через т. О (ОА= r), В этом случае плоскость отверстия МК будет разбита на зоны Френеля (в виде концентрических колец). Площади этих зон одинаковы и амплитуды волн исходящих от каждой зоны одинаковы. Однако амплитуды двух рядом находящихся зон отличаются по фазе на «Пи» и их общее действие равно нулю. Интенсивность света в максимумах по мере удаления от центральной точки будет убывать. Убывание объясняется тем, что при смещении точки наблюдения из центра на периферию открытые из центральной точки зоны Френеля частично «закрываются» и, кроме того, частично открываются новые зоны Френеля, ослабляющие интенсивность света в точке наблюдения. Если размер отверстия во много раз меньше первой зоны Френеля, то наблюдается размытое светлое пятно без каких либо колец. Если отверстие открывает «много» зон Френеля, то дифракционные кольца наблюдаются в узкой области на границе свет тень. А в остальной части экрана наблюдается практически равномерное освещение экрана, за исключением области геометрической тени, где освещённость отсутствует Дифракция наблюдается и для больших отверстий, но тогда должно быть и быть и большие расстояния от отверстия до экрана и от источника света до отверстия для получения условия зон Френеля как точечных источников света.
|
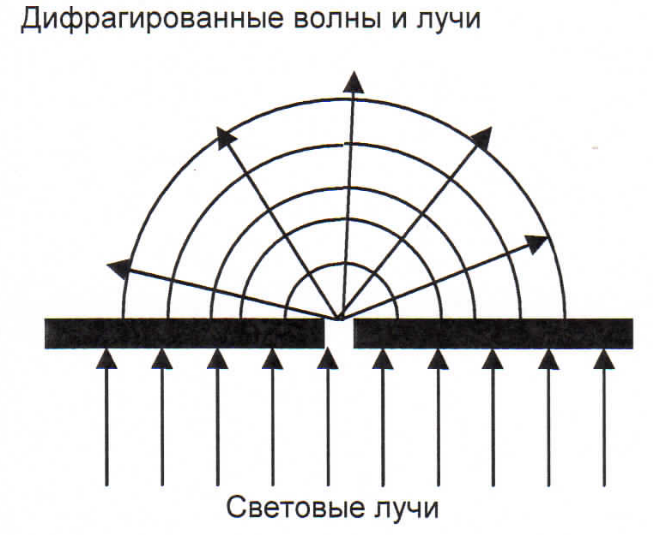
11. Дифракция в параллельных лучах (Фраунгофера).Дифракция плоских волн на щели. Вид дифракционной картины на экране. Условие дифракционного максимума и минимума при дифракции на щели. Тип дифракции, при котором дифракционная картина образуется параллельными пучками, называется дифракцией Фраунгофера. Параллельные лучи проявятся, если источник и экран находятся в бесконечности. Практически используется две линзы: в фокусе одной – источник света, а в фокусе другой – экран. Дифракция
на щели: Распределение
интенсивности света при дифракции на
щели: В качестве примера рассмотрим
дифракционную картину возникающую
при прохождении света через щель в
непрозрачном экране. Мы найдём
интенсивность света в зависимости от
угла в этом случае. Математическоепредставление
принципа Гюйгенса используется для
написания исходного уравнения.
Рассмотрим монохроматическую плоскую
волну с амплитудой пусть
(x′,y′,0) — точка внутри разреза, по
которому мы интегрируем. Мы хотим
узнать интенсивность в точке (x,0,z).
Щель имеет конечный размер в x направлении
(от
|
|
|
12. Дифракция от многих щелей. Дифракционная решетка. Условие дифракционного максимума и минимума при дифракции на решетке. Дифракционная картина от одной щели имеет несколько нечеткий вид. Получить более четкую картину можно получить, если использовать несколько щелей, причем , чем больше их, тем более резко разграничены максимумы. Система , состоящая из большого числа щелей, находящихся на одинаковом расстоянии Ь друг от друга, называют дифракционная решетка.
Дифракционная картина от одной щели имеет несколько нечеткий вид. Получить более четкую картину можно получить, если использовать несколько щелей, причем , чем больше их, тем более резко разграничены максимумы. Система , состоящая из большого числа щелей, находящихся на одинаковом расстоянии Ь друг от друга, называют дифракционная решетка. Сумму А1 + Ь = D называют постоянная решетки или период . Пусть при заданном угле «фи» каждая из щелей посылает свет в т. Р, т.е. в каждой щели будет одинаковое и при том нечетное число зон Френеля. Будет ли при этом в точке Р максимум или минимум зависит от наложения этих лучей. Из чертежа видно, что разность хода от двух щелей будет одинакова, какую пару из них не брать. Поэтому разность будет равнаΔr=d sinϕ
|
14. Равновесное тепловое излучение. Поток излучения,энергетическая светимость, спектральная плотность энергетической светимости. Коэффициенты поглощения. Абсолютно черное тело. Тепловым излучением называют излучение энергии тел, обусловленное возбужденными атомами или молекулами вследствие их теплового движения. При низких температурах тепловое движение состоит в основном из невидимого длинноволнового излучения: инфракрасные лучи от 7600 А до 2*107 А , а при более высоких температурах некоторую долю излучения составляют видимые световые (4000-7600 А) и невидимые ультрафиолетовые лучи (90-4000 А). Основные законы излучения, распространения и поглощения энергии одинаковы для всех лучей. Источником теплового излучения являются атомы и молекулы и оно связано с процессами, происходящими внутри их . Поэтому исследование теплового излучения является важнейшим способом проникновения в тайны строения атомов и молекул. Характерным отличием теплового излучения от других процессов излучений (например, люминесценции) является то, что распределение энергии между телом и излучением при данной температуре может не меняться, т.е. имеет место равновесное состояние, которое устойчиво. Излучение электромагнитных волн в системе находится в термодинамическом равновесии с телом и называется равновесным тепловым излучением. То есть если, допустим, имеется нагретое тело, находящееся внутри полости непроницаемой для излучения и кроме процесса излучения других процессов нет. Пусть нагретое тело испускает излучение в большом количестве, чем поглощает энергии, отраженной от стенок полости. Тогда тело будет постепенно охлаждаться и поток энергии от него будет уменьшаться до тех пор, пока количество поглощаемой и испускаемой энергий не сравняется. Аналогично можно рассуждать для того случая, когда тело излучает вначале меньше, чем поглощает. Свойства равновесного излучения: плотность лучистой энергии, ее распределение по спектру частот и направлениям не зависят от формы и материала стенок и определяется только температурой стенок. Оно однородно, изотропно и неполяризовано.
|
15. Дифференциальный и интегральный законы Кирхгофа. Закон Стефана-Больцмана, два закона Вина. Дифференциальный
закон Кирхгофа утверждает, что отношение
спектральной плотности энергетической
светимости тела к его монохроматическому
коэффициенту поглощения при данной
температуре и данной длине волны есть
величина постоянная, равная спектральной
плотности энергетической светимости
абсолютно черного тела при той же
температуре и той же длине волны:
Справедлив
закон Кирхгофа в интегральной форме:
отношение энергетической светимости
тела к его коэффициенту поглощения
не зависит от материала тела, а
определяется его температурой и равно
энергетической светимости абсолютно
черного тела при той же температуре.
Из законов Кирхгофа следует, что для абсолютно черного тела энергетическая светимость максимальна. Абсолютно черное тело поглощает при данной температуре волны всех длин, поэтому его спектры сплошные. Законы Стефана-Больцмана и Вина 1879
г. австрийский физик Стефан
эмпирически установил закон
зависимости энергетической светимости
абсолютно черного тела от температуры,
в 1884 г. Больцман е теоретически доказал:
По закону Стефана-Больцмана, где
|
|
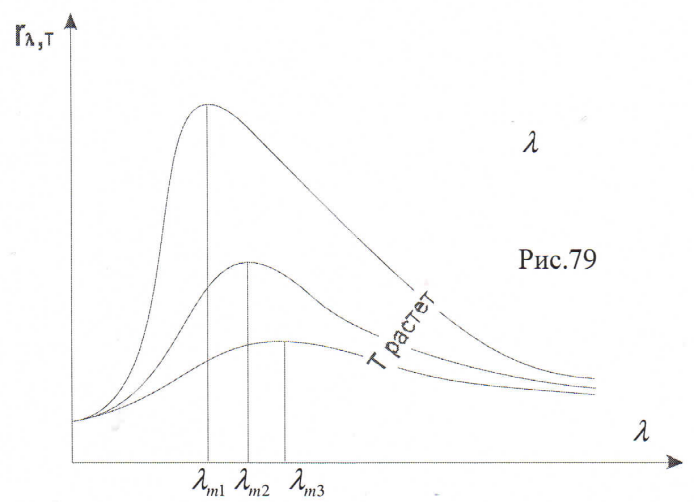
16. Распределение энергии в спектре излучения абсолютно черного тела - график.
Распределением энергии в спектре излучения абсолютно черного тела занимались Михельсон и Вин , последний использовал более точные методы измерения и анализа величины энергии, приходящейся на различные участки спектра и на каждую длину волны. Измерения производились с помощью термопары, один из спаев которой помещался в различные участки спектра. Анализ изотерм позволил сделать следующие выводы: 1.все кривые имеют при определенной длине и данной температуре максимум излучения энергии; 2.ординаты всех изотерм быстро растут с повышением температуры, что и должно было следовать из закона Стефана-Больцмана: энергетическая светимость графически выражается площадью изотермы; 3.при повышении температуры абсолютно черного тела длина волны, на которую приходится максимум энергии, смещается в сторону более коротких волн.
|
17. Квантовая гипотеза. Формула Планка. Масса и импульс фотона. Гипотеза
Планка
— при тепловом излучении энергия
испускается и поглощается не непрерывно,
а отдельными квантами (порциями).
Каждая такая порция-квант имеет
энергию
Фотон — элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя. Масса
фотона выводится из формулы :
mмасса фотона,кгhпостоянная Планка, 6,626176 × 10-34Дж × сνчастота излучения,Гц λдлина волны излучения,мcскорость света в вакууме,м/с Используя
формулу массы фотона, можно получить
формулу импульса фотона р = mc.
|
18. Фотоэффект (внешний и внутренний). Законы Столетова для фотоэффекта. Уравнение Эйнштейна для фотоэффекта. Применение фотоэффекта. Внешним фотоэлектрическим эффектом (фотоэффектом) называется испускание электронов веществом под действием электромагнитного излучения. Внешний фотоэффект наблюдается в твердых телах, а так же в газах на отдельных атомах и молекулах. Внутренним фотоэффектом называется перераспределение электронов по энергетическим состояниям в твердых и жидких полупроводниках и диэлектриках, происходящее под действием излучений. Он проявляется в изменении концентрации носителей зарядов в среде и приводит к возникновению фотопроводимости или вентильного фотоэффекта. Фотопроводимостью называется увеличение электрической проводимости вещества под действием излучения. Законы Столетова: 1.
При фиксированной частоте падающего
света число фотоэлектронов, вырываемых
из катода в единицу времени,
пропорционально интенсивности света
(сила фототока насыщения пропорциональна
энергетической освещенности
2.Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой v. 3. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.
Применение фотоэффекта:вакуумные фотоэлементы, которые нашли разнообразное применение в различных областях науки и техники (фотореле, люксметры, системы звукозаписи на пленку и др.). Он представляет собой откачанный стеклянный баллон, внутренняя поверхность покрыта фоточувствительным слоем, служащим фотокатодом. В качестве анода обычно используется кольцо или сетка, помещаемая в центре баллона. Кремниевые и другие вентильные фотоэлементы применяются для создания солнечных батарей, непосредственно преобразующих световую энергию в электрическую. Такие батареи уже в течение многих лет работают на советских космических спутниках и кораблях, их КПД приблизительно 10% и, как показывают теоретические расчеты, может быть доведён до 22%, что открывает широкие перспективы использования в качестве источников для бытовых и производственных нужд. Рассмотренные виды фотоэффекта нашли применение в производстве для контроля, управления и автоматизации различных процессов, в военной технике сигнализации и локации невидимым излучением, в технике звукового кино, в различных системах связи и т.д. |
|
19. Ядерная модель атома. Опыты Резерфорда по рассеиванию а- частиц. Ядерная модель атома Резерфорда. Недостатки модели Резерфорда. Опыты Резерфорда по рассеянию α-частиц: Резерфорд, исследуя прохождение α-частиц в веществе (через золотую фольгу толщиной примерно 1 мкм), показал, что основная их часть испытывает незначительные отклонения, но некоторые α-частицы (примерно одна из 20 000) резко откланяться от первоначального направления.Т.к. электроны не могут существенно изменить движение столь тяжёлых и быстрых частиц, как α-частица, то Резерфордом был сделан вывод, что значительное отклонение α-частиц обусловлено их взаимодействием с положительным зарядом большой массы. Это, в свою очередь, означает, что положительный заряд атома сосредоточен в объёме, очень малом по сравнению с объёмом атома. На основании своих исследований Резерфорд предложил ядерную(планетарную) модель атома. Согласно этой модели, вокруг положительного ядра, имеющего заряд Z_e (Z - порядковый номер в таблицы Менделеева, e–элементарный заряд) по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Противоречия: 1) В теории было сплошным, а практике линейным движением 2) Атом - стабильная частица, не может двигаться по сторонам. |
20. Закономерности в спектре излучения атомарного водорода. Спектральные серии Лаймана, Бальмера и Пашена Как известно, если вещество нагреть достаточно сильно в пламени или дуге, то обычно оно дает излучение главным образом в видимой и ультрафиолетовой части спектра. Причем спектр состоит из определенной последовательности линий, которые и характеризуют данный элемент (линейчатые спектры). Он обычно называется атомным спектром, т.к. зарождается в атомах. В результате многих исследований были определены длины волн большинства линейчатых спектров элементов. Подобно
другим элементам спектр атомарного
водорода тоже линейчатый. Оказалось,
что весь спектр можно разбить на группы
линий, которые назвали сериями. Бальмер
показал, что длины волн линий, входящих
в видимую и близкую ультрафиолетовую
области спектра удовлетворяют некоторой
формуле Группа линий, находящихся в глубокой ультрафиолетовой части спектра, была объединена в серию Лаймана и оказалось, что для нее тоже можно подобрать расчетную формулу, по которой можно вычислить длину волны любой линии этой серии. Далее
были обнаружены 4 серии в инфракрасной
части спектра:серииПашена, Брэкета,
Пфунда, Хэмфри и для этих серий тоже
можно получить соответствующие
формулы. Анализируя формулы всех
серий, Ритберг показал, что их все
можно объединить в одну формулу,
охватывающую все линии, наблюдаемые
в спектре. Эту формулу называют формулой
Бальмера-Ритберга Точность, с которой значения длин волн, вычисленные по этой формуле, совпадали с результатами их измерений на опыте, была настолько высока, что совершенно исключалось предположение о случайном совпадении. |
21. Постулаты Бора. Первый
постулат Бора
(постулат стационарных состояний): В
атоме существуют стационарные (не
изменяющиеся со временем) состояния,
в которых он не излучает энергии.
Стационарным состояниям атома
соответствуют стационарные орбиты,
по которым движутся электроны. Движение
электронов по стационарным орбитам
не сопровождается излучением
электромагнитных волн.
В стационарном
состоянии атома электрон, двигаясь
по круговой орбите, должен иметь
дискретные квантованные значения
момента импульса, удовлетворяющие
условию Второй
постулат Бора(правило
частот): При переходе электрона с одной
стационарной орбиты на другую излучается
(поглощается) один фотон с энергией:
|
|
22. Теория атома водорода по Бору. Радиусы электронных орбит и скоростей электронов в атоме водорода. Энергия стационарного состояния атома водорода. С
учетом постулатов Бора условие
обращения электрона на и - той орбите
может быть записано ввиде 2-хуравнений:
Энергия
стационарного состояния атома водорода
складывается из кинетической энергии
электрона и взаимной потенциальной
энергии электрона и ядра. В результате
можно получить формулу полной энергии
электрона на n
- той орбите
25.
Естественная радиоактивность,
Радиоактивность- испускание радиоактивного излучения. В настоящее время под радиоактивностью понимают способность некоторых атомных ядер самопроизвольно (спонтанно) превращаться в другие ядра с испусканием различных видов радиоактивных излучений и элементарных частиц. Естественнаянаблюдается у неустойчивых изотопов, существующих в природе.
Закон
радиоактивного распада:
|
23. Излучение атома водорода по Бору. Обобщенная формула Бальмера.
Обобщенная
формула
Бальмера:
Квант
излучаемой энергии
при переходе с удаленной орбиты k
на ближнюю орбиту n
равен
|
24. Состав атомного ядра. Изотопы, изобары, изотоны.Дефект массы и энергия связи ядра, удельная энергия связи. Свойства ядерных сил. Ядро
атома состоит из нуклонов, которые
подразделяются на протоны и
нейтроны.Обозначение ядра атома: А- число нуклонов, т.е. протонов + нейтронов ( или атомная масса )Z- число протонов ( равно числу электронов ) N- число нейтронов ( или атомный номер )N = A–Z Атомы с одинаковыми атомными номерами называют изотопами: в таблице Менделеева они расположены в одной клеточке.Изобары, атомы различных химических элементов с одинаковым массовым числом А. Ядра И. содержат равное число нуклонов, но различные числа протонов Z и нейтронов N.Изотоны— нуклиды, имеющие одинаковое количество нейтронов, но различающиеся по числу протонов в ядре. Дефект массы — разность между массой покоя атомного ядра данного изотопа, выраженной в атомных единицах массы, и массовым числом данного изотопа. В современной науке для обозначения этой разницы пользуются термином избыток массы. Как правило, избыток массы выражается в кэВ.
Энергией связи называют энергию, равную работе, которую надо совершить, чтобы расщепить ядро на свободные нуклоны.Е связи = - А Энергия связи ядра численно равна работе, которую нужно затратить для расщепления ядра на отдельные нуклоны, или энергии, выделяющейся при синтезе ядер из нуклонов.Мерой энергии связи ядра является дефект массы. Формула
для расчета энергии связи ядра - это
формула Эйнштейна: если есть какая-то
система частиц, обладающая массой, то
изменение энергии этой системы приводит
к изменению ее массы. ЯДЕРНЫЕ СИЛЫ- действуют между всеми нуклонами в ядре;- силы притяжения;- короткодействующие. Удельная энергия связи - это энергия связи, приходящаяся на один нуклон.
|
|
26.
Правила смешения при а и
Где
Радиоактивные семейства (ряды) - генетически связанные последовательным радиоактивным распадом цепочки (ряды) ядер естественного происхождения. |
27. Активность радиоактивного-вещества. Единицы ее измерения. Активностью А нуклида в радиоактивном источнике называется число распадов, происходящих
с ядрами образца в 1 с:
|

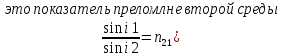
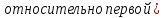 .Этот
показатель равен отношению их абсолютных
показателей преломления.
.Этот
показатель равен отношению их абсолютных
показателей преломления.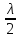
 2
2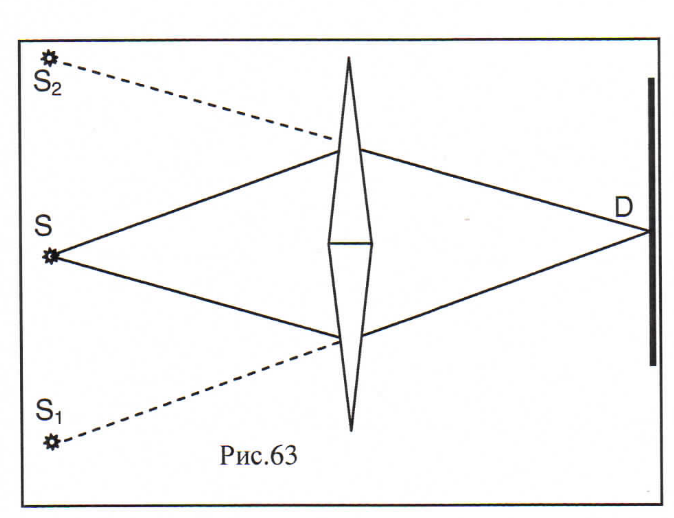
 3
3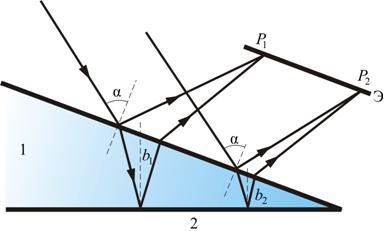
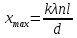 Минимум
(темная полоск а)
Минимум
(темная полоск а)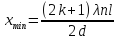
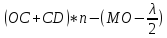
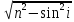 +
+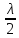
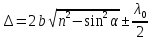 ,
подставляя в неё толщину пленки в
месте падения луча (
,
подставляя в неё толщину пленки в
месте падения луча (
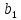 или
или ). Свет обязательно должен быть
параллельным (
). Свет обязательно должен быть
параллельным (
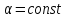 ): если одновременно будут изменяться
два параметра b и α, то устойчивой
интерференционной картины не будет.
): если одновременно будут изменяться
два параметра b и α, то устойчивой
интерференционной картины не будет. —
max, где m-
любое целое число, λ
- длина волны.
—
max, где m-
любое целое число, λ
- длина волны.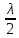 —
min
—
min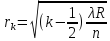 гдеR
— радиус кривизны линзы;
гдеR
— радиус кривизны линзы;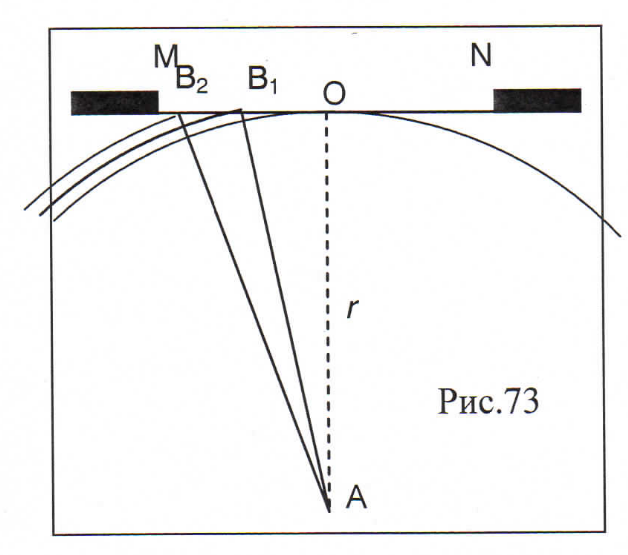
 при переходе от зоны к зоне:
при переходе от зоны к зоне: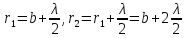 ,
,
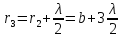
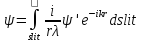
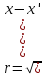 ,
,
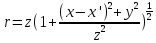 . bsin
. bsin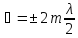 -
условие минимума
-
условие минимума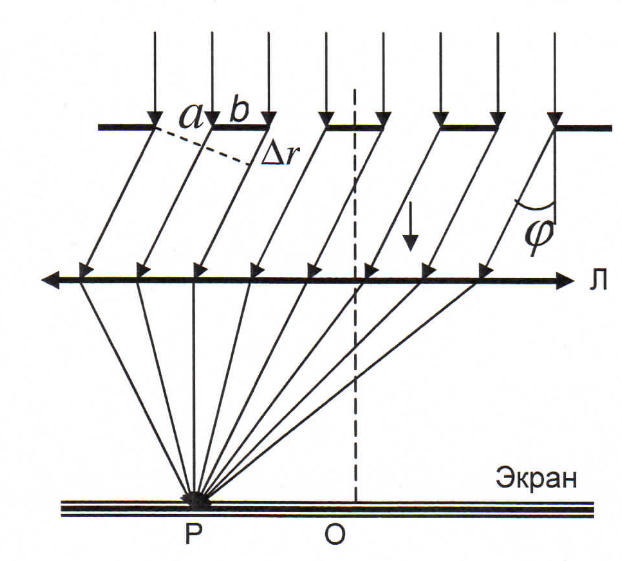
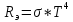 -
постоянная Стефана-Больцмана.
-
постоянная Стефана-Больцмана.
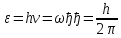 ,
h -коэффициент пропорциональности,
названный впоследствии постоянной
Планка. На основе этой гипотезы он
предложил теоретический вывод
соотношения между температурой тела
и испускаемым этим телом излучением
— формулу Планка. Позднее гипотеза
Планка была подтверждена экспериментально.
Выдвижение этой гипотезы считается
моментом рождения квантовой механики.
,
h -коэффициент пропорциональности,
названный впоследствии постоянной
Планка. На основе этой гипотезы он
предложил теоретический вывод
соотношения между температурой тела
и испускаемым этим телом излучением
— формулу Планка. Позднее гипотеза
Планка была подтверждена экспериментально.
Выдвижение этой гипотезы считается
моментом рождения квантовой механики.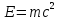 используя
одновременно формулы Энергия кванта
и Уравнение Эйнштейна, получаем hν =
mc2.
Отсюдаm=
используя
одновременно формулы Энергия кванта
и Уравнение Эйнштейна, получаем hν =
mc2.
Отсюдаm=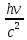 Поскольку
с = λν,
имеем
Поскольку
с = λν,
имеем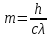
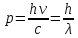
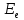 катода).
катода).
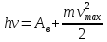 - уравнение
Эйнштейна для фотоэффекта.
- уравнение
Эйнштейна для фотоэффекта.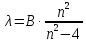 где
В - постоянная, а n
для различных линий серии принимает
ряд чисел, начиная с трех:3,4,5, Всего в
серии (ее назвали серией Бальмера)
находится 25 линий.
где
В - постоянная, а n
для различных линий серии принимает
ряд чисел, начиная с трех:3,4,5, Всего в
серии (ее назвали серией Бальмера)
находится 25 линий. 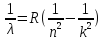 где
и - целое число, характеризующее серию:
для серии Лайманаn=l,
серии Бальмераn=2,
серии Пашенаn=3,
Пфундаn=4;
Хэмфри n=5
k-
- целые числа, начиная с двух; R–
постоянная Ритберга (R=
1,1 1
где
и - целое число, характеризующее серию:
для серии Лайманаn=l,
серии Бальмераn=2,
серии Пашенаn=3,
Пфундаn=4;
Хэмфри n=5
k-
- целые числа, начиная с двух; R–
постоянная Ритберга (R=
1,1 1 c
c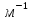 ).
).
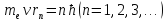 ,
где
,
где
 -масса
электрона, м-его скорость по n-й
орбите радиуса
-масса
электрона, м-его скорость по n-й
орбите радиуса
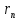 ;
;
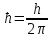
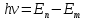 ,
равной разности энергий соответствующих
стационарных состояний. При
,
равной разности энергий соответствующих
стационарных состояний. При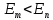 происходит излучение фотона, при
происходит излучение фотона, при
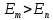 – его поглощение. Набор возможных
дискретных частот
– его поглощение. Набор возможных
дискретных частот
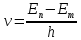 квантовых переходов и определяет
линейчатый спектр атома.
квантовых переходов и определяет
линейчатый спектр атома.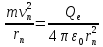 и
и
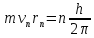 .
Учитывая, что заряд ядра Q=Zе из этих
уравнений можно получить выражение
для скорости
.
Учитывая, что заряд ядра Q=Zе из этих
уравнений можно получить выражение
для скорости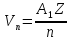 ,
для радиуса орбиты
,
для радиуса орбиты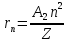 ,
где A1
и A2
константы.
,
где A1
и A2
константы.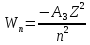
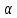 ,
,
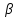 .
.
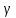 -лучи.
Закон радиоактивного распада. Период
полураспада.
-лучи.
Закон радиоактивного распада. Период
полураспада.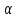 -Излучение
представляет собой поток ядер гелия;
заряд
-Излучение
представляет собой поток ядер гелия;
заряд
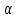 -частицы равен +2е, а масса совпадает
с массой ядра изотопа гелия
-частицы равен +2е, а масса совпадает
с массой ядра изотопа гелия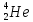 .
. 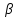 -Излучение
представляет собой поток быстрых
электронов (это вытекает из определения
их удельного заряда).
-Излучение
представляет собой поток быстрых
электронов (это вытекает из определения
их удельного заряда). 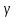 -Излучение
представляет собой коротковолновое
электромагнитное излучение с чрезвычайно
малой длиной волны
-Излучение
представляет собой коротковолновое
электромагнитное излучение с чрезвычайно
малой длиной волны
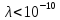 м
и вследствие этого — ярко выраженными
корпускулярными свойствами, т.е.
является потоком частиц —
м
и вследствие этого — ярко выраженными
корпускулярными свойствами, т.е.
является потоком частиц —
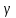 -квантов (фотонов).
-квантов (фотонов).
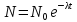 ,
где
,
где
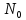 -начальное
число нераспавшихся ядер(в момент
времени t=0),
N-число
нераспавшихся ядер в момент времени
t.
Период
полураспада
-начальное
число нераспавшихся ядер(в момент
времени t=0),
N-число
нераспавшихся ядер в момент времени
t.
Период
полураспада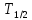 — время, за которое исходное число
радиоактивных ядер в среднем уменьшается
вдвое.
— время, за которое исходное число
радиоактивных ядер в среднем уменьшается
вдвое.
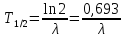 Периоды полураспада для
естественно-радиоактивных элементов
колеблются от десятимиллионных долей
секунды до многих миллиардов лет.
Периоды полураспада для
естественно-радиоактивных элементов
колеблются от десятимиллионных долей
секунды до многих миллиардов лет.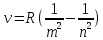 ,
где m-постоянное
значение в серии, n-определяет
отдельные линии этой серии, R=
,
где m-постоянное
значение в серии, n-определяет
отдельные линии этой серии, R=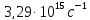
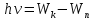
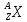

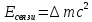
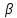 -распадах.Радиоактивные
семейства..
-распадах.Радиоактивные
семейства..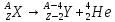 для
α–распада
для
α–распада 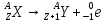 для
для
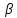 –распада
–распада 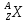 –
материнское ядро, Y
– символ дочернего ядра,
–
материнское ядро, Y
– символ дочернего ядра,
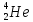 - ядро гелия(
- ядро гелия(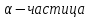 ),
),
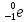 -
символическое обозначение электрона.
-
символическое обозначение электрона.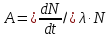 ,единицаактивности
– беккерель (Бк): 1Бк – активность
нуклида, при которой за 1 с происходит
один акт распада. Внесистемная единица
активности в радиоактивном источнике
– кюри (Ки): 1Ки=
,единицаактивности
– беккерель (Бк): 1Бк – активность
нуклида, при которой за 1 с происходит
один акт распада. Внесистемная единица
активности в радиоактивном источнике
– кюри (Ки): 1Ки=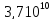 Бк
Бк