Лабораторная работа № 10

МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО

СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РСФСР

Новосибирский ордена Трудового Красного Знамени

инженерно-строительный институт им. В.В.Куйбышева

Кафедра физики

Лабораторная работа № 10

Определение коэффициента восстановления,

времени соударения и силы удара взаимодействующих тел

НОВОСИБИРСК 1990

Во многих случаях взаимодействия тел мы сталкиваемся с этой разновидностью – ударом. В частности, в строительстве – это работы по забивке свай, применение пневмомолотков и т. д. Поэтому весьма важно изучение физической стороны удара и процессов, происходящих при этом в телах.

Удар – это совокупность явлений возникающих при кратковременном приложении к телу внешних сил и связанных с изменением его скорости. При этом мерой взаимодействия тел служит изменение импульса (количества движения) тела, связанного с импульсом тела:

.

Рассеяние механической энергии при ударе характеризуется коэффициентом восстановления скорости (k_c) или коэффициентом восстановления энергии (k_э).

Коэффициент восстановления скорости определяется по формуле:

, (1)

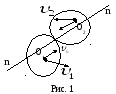
где υ_1n и υ_2n – проекции на линию удара скоростей первого и второго тел до удара (рис. 1);

U_1n и U_2n – проекции тех же тел после удара.

При центральном ударе линия удара совпадает с линией О₁О₂, соединяющей центры масс тел и тогда υ_1n = υ₁: U_1n = U₁ и т.д. Следовательно выражение (1) переписывается в виде

, (2)

Если υ₁=0 и U₁=0, то есть первое тело массивное и неподвижное, как это осуществлено в этой работе, то

. (3)

Коэффициент восстановления энергии зависит от системы отсчёта и определяется как отношение суммарной кинетической энергии тел после удара (Е''_к) к суммарной кинетической энергии тел до удара (Е'_к).

. (4)

Величины коэффициентов восстановления зависят от физических свойств материалов соударяющихся тел, их формы, массы.

Для абсолютно неупругого удара k_э=0, а для абсолютно упругого k_э=1, для реальных случаев 0<k_э<1.

В представленной работе коэффициенты считаются зависящими только от материала соударяющихся тел. В качестве их используется шар, подвешенный на проволоках и массивный стальной куб, на котором закрепляются пластины из различных металлов (медь, алюминий свинец и бронза).

Для отклонённого на угол α₀ шара (поднятого над начальным положением на высоту h₀) можно записать, что

, или , (5)

где h₀ – высота подъема шара над начальным положением.

Так как

, (6)

Тогда можно записать, что до удара

. (7)

После удара шара о неподвижный куб, шар отскочит на угол α₁, и можно получить аналогичное энергетическое уравнение после удара:

. (8)

Теперь можно по формулам (3) и (4) найти коэффициент восстановления. Уменьшение угла отклонения после первого удара может быть небольшим, если соударение близко к упругому и погрешность результата при этом резко возрастает. Для её уменьшения целесообразно измерять величину угла после n отскоков шара от куба. Тогда можно записать систему уравнений, дополнительных к (7) и (8):

; ; … (9)

Коэффициент восстановления энергии для первого удара для второго удара и т.д. Перемножим эти равенства:

; . (10)

Аналогично соотношения можно записать для коэффициента восстановления скорости:

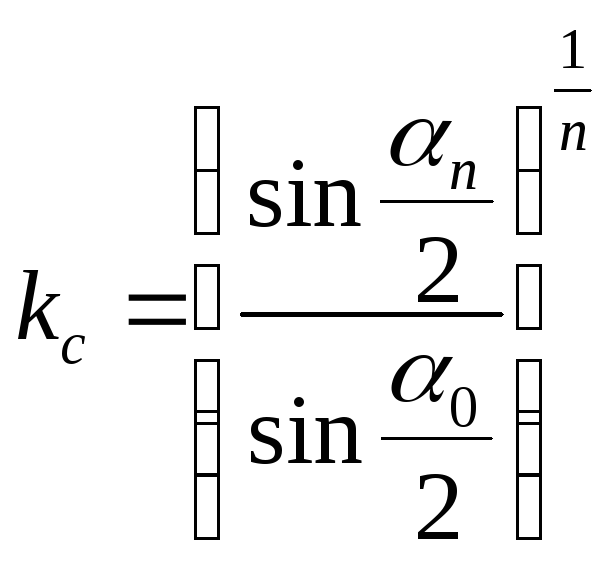(11)

или

. (12)

Время соударения тел также зависит от многих факторов: относительной скорости тел, их размеров, упругих свойств материалов и т.д. В случае соударения металлических тел оно может быть измерено электрическим методом. Для этого используем схему, приведённую на рис. 2.

В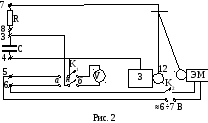 положении "А" ("заряд ёмкости") конденсатор С заряжается до значения напряжения V₀ на нём. Если перевести переключатель в положение "Н" ("нейтральное положение") и произвести соударение (замыкание 12 и 3), то часть заряда нейтрализуется и напряжение на нём станет равным V₀. Так же как и в случае определения коэффициентов k_c и k_э , значение второго напряжения может мало отличаться от начального (V₀). Для повышения точности необходимо после того, как произойдёт первое соударение, успеть задержать шар, вернуть его в начальное положение, отклонить на тот же угол и повторить удар, не подзаряжая конденсатор. Теория электрического разряда в цепи, содержащей R и C, которая здесь не рассматривается, позволяет определить время среднего соударения при n соударениях в одном и том же исходном положении тел:

. (13)

Зная время соударения, можно рассчитать среднюю силу удара за промежуток действия:

; .

Так как

,

то

, (14)

где l – длина полвеса (по перпендикуляру от точки подвеса до центра шара).

ОПИСАНИЕ УСТАНОВКИ

Установка состоит из массивного основания (1), на котором закреплена стойка (4) с кронштейном (6) и стержнем (5). К стержню на нитях подвешен стальной шар (12). Его можно отводить вдоль шкалы (9) на углы от 0⁰ до 50⁰ от вертикального положения и фиксировать за счёт притяжения электромагнита (8), укреплённого на штанге (7). На основании установки размещён куб (3) с закреплёнными на нём образцами различных материалов. Куб поворачивается вокруг оси и фиксируется так, чтобы его плоскость была перпендикулярна направлению удара. На горизонтальной поверхности основания расположены клеммы для подключения измерительного прибора, батареи, выключатель электромагнита и переключатель «заряд – работа».

ХОД РАБОТЫ

Задание I: Определение коэффициентов восстановления энергии и скорости.

1. Подключить источник питания (6 В) к клеммам «батарея».

2. Зафиксировать куб на оси так, чтобы с шаром взаимодействовал стальной образец (отвернув и завернув головку 10).

3. Отвести штангу (7) с электромагнитом (8) и зафиксировать её в положении, при котором будет обеспечен угол отклонения α₀ шарика порядка 30⁰ – 40⁰ и при движении шарик не задевал прозрачной шкалы (9), для этого можно воспользоваться установочными винтами II. Включить питание электромагнита (ключ К), ввести шар в контакт с электромагнитом.

4. Выключить электромагнит, отсчитать 5 – 10 ударов шара об образец и заметить угол α_n после n – ного отскока.

5. Повторить операции, указанные в пунктах 3 и 4 ещё несколько (4 – 6) раз, меняя каждый раз значение начального угла α₀.

6. Рассчитать среднее значение k_с и k_э по формулам (II) и (12). Данные внести в таблицу I.

Таблица 1

№ п/п	α0	n	α0	kc	kэ
1 2 3
ср.

Задание II : Определение времени соударения и средней силы удара.

1. С учётом полярности подключить к клеммам "6" "измерение" – вольтметр (или гальванометр).

2. Включить электромагнит и ввести шар в соприкосновение с ним.

3. Перевести переключатель К₂ в положение «а», а затем в «б», измерив тем самым максимальное напряжение на конденсаторе (V₀).

4. Снова зарядить конденсатор (в положении «а»), но после этого поставить переключатель в нейтральное положение «Н».

5. Теперь выключить электромагнит и осуществить одиночное соударение, не дав шару после отскока вновь удариться об образец, а отвести его назад к электромагниту, снова произвести соударение и так проделать несколько раз (число n в формуле (13)). Только после этого можно перевести переключатель в положение «б» и определить оставшееся напряжение на конденсаторе.

Наибольшая точность получится, если применить импульс цифровой вольтметр, например, типа Щ 1413, на котором должна быть нажата клавиша «10 В», а остальные находиться в отжатом состоянии. В этом случае после переключения в положении «б», запомнить число на табло вольтметра (дальше они будут меняться).

6. Повторить пункты 2 – 4 для других отклонений (не менее 5 – 6 значений), например 30⁰; 25⁰; 15⁰; 10⁰.

7. Вычислить τ и F для заданных углов.

8. Построить график зависимости F от угла отклонения. Данные представить в таблицу 2.

Таблица 2

№ п/п	α0	n	U0	Un	τ	F
1 2 3
ср.

9. Вычислить доверительные интервалы для значений k_э и τ.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое импульс силы и импульс тела?

2. Сформулируйте закон сохранения импульса тела для замкнутой системы.

3. Сформулируйте и запишите закон сохранения механической энергии для замкнутой системы.

4. Как записываются оба эти закона для абсолютно упругого и абсолютно неупругого ударов?

5. Дайте определение взаимодействия типа "удар".

6. Как отличить внешне неупругое взаимодействие от упругого?

7. Что такое коэффициент восстановления скорости и коэффициент восстановления энергии?

8. Почему для определения коэффициентов восстановления берут серию ударов?

9. На каком принципе основан метод определения времени соударения шаров в данной работе?

10. На основании какого физического закона выводится формула определения силы удара?

9