29

Вычисляя сумму элементарных работ двух внутренних сил F1 J и F2J ,

получаем

F1J dS1 cos(P1 J ,υ1 )+ F2J dS2 cos(P2 J ,υ2 )= F1′M1M1′ − F1M 2 M 2′

т.к. каждой внутренней силе соответствует другая, равная ей по модулю и противоположная по направлению, то сумма элементарных работ всех внутренних сил тоже равна нулю.

δAJ = ∑δAiJ = 0

Конечное перемещение является совокупностью элементарных переме-

щений, поэтому AJ = 0, т.е. сумма работ внутренних сил твердого тела на любом его перемещении равна нулю.

2.5.2. Работа внешних сил, приложенных к поступательно движущемуся телу

К каждой точке тела приложены внешние и внутренние силы (рис. 18). Так как работа внутренних сил на любом перемещении равна нулю, то следует вычислить работу лишь внешних сил F1 E , F2E … FnE . При поступательном

движении траектории всех точек идентичны, а вектора элементарных перемещений геометрически равны, т.е.

dri = dr = drc .

Элементарная работа силы Fi E

δAiE = Fi E drc .

Элементарная работа всех внешних сил

δAE = ∑δAiE = ∑F iE drc = drc ∑Fi E = R E drc ,

где R E - главный вектор внешних сил.

Работа на конечном перемещении

(2 )

AE = ∫R E drc .

(1)

Работа сил при поступательном перемещении твердого тела равна работе главного вектора внешних сил на элементарном перемещении центра масс.

2.5.3. Работа внешних сил, приложенных к вращающемуся телу

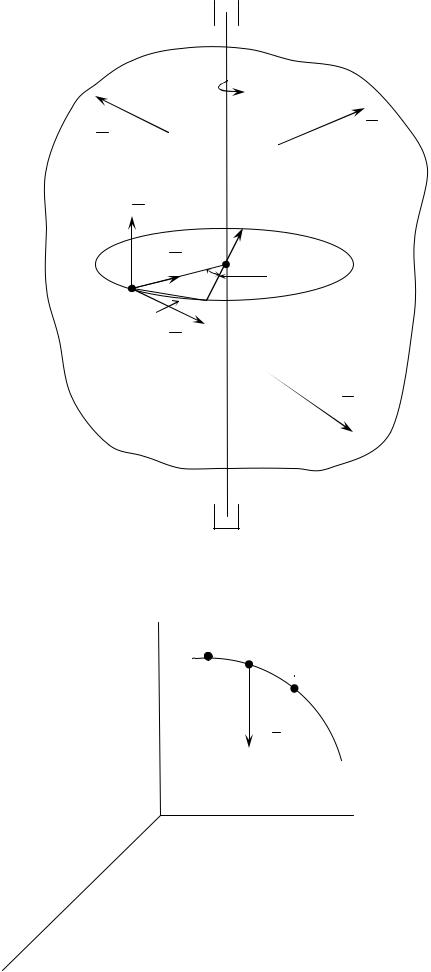
Предположим, что к твердому телу, вращающемуся вокруг неподвижной оси Z , приложены внешние силы F1 E , F2E … Fi E … FnE (рис. 19).

Вычислим работу одной силы Fi E , приложенной к точке Mi , описывающей окружность радиуса Ri . Разложим силу Fi E на три составляющие, направленные по естественным осям траектории точки Mi .

31

При элементарном повороте тела на угол dϕ точка Mi описывает дугу dSi = Ri dϕ . На этом перемещении работу составляет только касательная составляющая силы, а работа перпендикулярных к вектору скорости составляющих силы FinE и FibE равна нулю.

δAiE = FiτE dSi = FiτE Ri dϕ = MiEτ dϕ = MizE dϕ , т.к. моменты нормальной и бинормальной составляющих силы Fi E относительно оси Z равны нулю эле-

ментарная работа всех сил, приложенных к твердому телу

δAE = ∑δAiE = ∑M izE dϕ = dϕ∑MizE = M zE dϕ .

Таким образом, элементарная работа внешних сил, приложенных к вращающемуся твердому телу равна

δAE = M zE dϕ .

При конечном повороте тела работа внешних сила равна

ϕ2

AE = ∫M zE dϕ .

ϕ1

Если главный момент внешних сил M zE = const , то работа внешних сил на конечном перемещении равна A = M zE (ϕ2 −ϕ1 ).

Работа при вращательном движении твердого тела равна работе главного момента внешних сил относительно оси вращения на элементарном угловом перемещении.

2.6. Работа силы тяжести

Пусть точка массой m перемещается под действием силы тяжести из положения M1 (x1 , y1 ,z1 ) в положение M 2 (x2 , y2 ,z2 ) (рис. 20).

Элементарная работа силы вычисляется как скалярное произведение вектора силы F (X ,Y ,Z ) на вектор элементарного перемещения dr (dx,dy,dz)

δA = F dr = Xdx +Ydy + Zdz ,

где X ,Y ,Z - проекции силы F ,

dx,dy,dz - проекции вектора перемещения dr на оси x, y,z . При движении под действием силы тяжести

А= ±mgh .

Если точка опускается (независимо от вида траектории), т.е. z2 < z1 , работа силы тяжести положительна, если точка поднимается, работа силы тя-

32

жести отрицательна. Если точка перемещается горизонтально (z2 = z1 ), работа силы тяжести равна 0.

3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ

Рассмотрим материальную точку M массой m , движущуюся под дей-

Умножим обе части уравнения на dS и проинтегрируем обе части равенства в пределах, соответствующих начальному и конечному положениям

из положения M1 в положение M 2 .

33

V

F 1

Рис. 21

Vi 2

Mi2

Mi

Vi1

J

Fi

Рис. 22