
- •РАЗДЕЛ 1. КИНЕМАТИКА
- •Введение
- •1. ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ
- •2. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- •2.1. Поступательное движение твердого тела
- •2.2. Вращательное движение твердого тела
- •2.2.1. Угловая скорость и угловое ускорение
- •2.2.2. Скорость и ускорение точки вращающегося тела
- •2.2.3. Векторное выражение скорости, центростремительного и вращательного ускорений точек вращающегося тела
- •3. ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- •3.1. Разложение плоского движения на простейшие
- •3.2. Теорема сложения скоростей при плоском движении
- •3.3. Мгновенный центр скоростей
- •3.4. Определение скоростей точек тела плоской фигуры с помощью мгновенного центра скоростей
- •Решение
- •Пример 2
- •Расстояния
- •Решение
- •РАЗДЕЛ II. ДИНАМИКА
- •Введение
- •1. ДИНАМИКА СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- •1.1. Основные законы динамики
- •2. Динамика механической системы
- •2.1. Масса механической системы. Центр масс
- •2.2. Моменты инерции твердого тела. Радиус инерции
- •2.3. Классификация сил, действующих на механическую систему
- •2.4. Работа силы
- •2.5. Работа сил, приложенных к твердому телу
- •2.5.1. Работа внутренних сил
- •2.5.3. Работа внешних сил, приложенных к вращающемуся телу
- •2.6. Работа силы тяжести
- •3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- •4. ТЕОРЕМА ОБ ИЗМЕНЕИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- •5.1. Пример решения задачи на теорему об изменении энергии механической системы
- •Содержание задачи
- •Схема механической системы
- •6. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
- •6.1. Связи и их уравнения
- •6.2. Классификация связей
- •6.4. Принцип возможных перемещений
- •6.5. Пример решения задачи на принцип возможных перемещений
- •Содержание задачи
- •Литература
1
Министерство образования и науки Российской Федерации Нижегородский государственный архитектурно-строительный университет
Институт открытого дистанционного обучения
Аистов А.С., Баранова А.С., Трянина Н.Ю.
Теоретическая механика
Часть II. Кинематика и динамика твердого тела
Утверждено редакционно-издательским советом университета
в качестве учебного пособия
Нижний Новгород – 2004
2
ББК 22.21 Т 11
Аистов А.С., Баранова А.С., Трянина Н.Ю. Теоретическая механика. Часть II. Кинематика и динамика твердого тела. Учебное пособие.– Н.Новгород: Нижегорд. гос. архит.-строит. ун-т., 2004.– 69 с.
ISBN 5-87941-303-9
Учебное пособие содержит основные сведения и теоретические положения кинематики и динамики твердого тела. Включает задания для контрольных работ по кинематике и динамике, краткие сведения из теории, рекомендации по решению задач, примеры решения типичных задач.
ББК 22.21
ISBN 5-87941-303-9
© коллектив авторов, 2004 © ННГАСУ, 2004
3
РАЗДЕЛ 1. КИНЕМАТИКА
Введение
Кинематика – это раздел теоретической механики, в котором изучается механическое движение, т.е. изменение положения одного тела относительно другого тела, с которым связана система отсчета, которая может быть как движущейся, так и неподвижной, без учета действующих сил.
Относясь к разделу фундаментальных наук, теоретическая механика и кинематика как важная составная часть ее, является основой для изучения многих дисциплин, изучающихся в высшей технической школе.
Законы и методы теоретической механики находят широкое применение в изучении важнейших задач техники, таких как конструирование различных сооружений, машин и механизмов, изучение движения космических тел, решение задач аэродинамики, баллистики и других.
Теоретическая механика, основанная на трудах Аристотеля, Архимеда, Галилея, Ньютона, носит название классической механики, в ней рассматривается движение тел со скоростями, много меньшими скорости света.
Механическое движение происходит во времени в пространстве, при этом в классической механике пространство считается трехмерным, подчиняющимся евклидовой геометрии; время считается протекающим непрерывно и одинаково во всех системах отсчета.
1. ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ
Все кинематические величины, характеризующие движение тела или его отдельной точки (расстояние, скорости, ускорения и т.д.) рассматриваются как функции времени.
Решить задачу кинематики значит найти траекторию, положение, скорость и ускорение каждой точки тела.
Траектория точки – это геометрическое место последовательных положений, занимаемых точкой в пространстве при ее перемещении.
Скорость точки – это векторная величина, характеризующая быстроту изменения положения точки в пространстве.
Ускорение точки – это векторная величина, характеризующая быстроту изменения скорости.

4
2.ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
2.1.Поступательное движение твердого тела
Поступательным называется такое движение твердого тела, при котором отрезок соединяющий две любые точки тела перемещаются параллельно самому себе.
При поступательном движении твердого тела скорости и ускорения всех точек тела геометрически равны и траектории всех точек идентичны, т.е. при наложении совпадают, поэтому достаточно точно знать характеристики движения одной точки тела.
2.2.Вращательное движение твердого тела
2.2.1.Угловая скорость и угловое ускорение
Вращательным называется движение твердого тела, при котором остаются неподвижными хотя бы две точки тела. Прямая, проходящая через эти точки, называется осью вращения. Все точки тела, лежащие на оси, при вращении остаются неподвижными. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на оси, а радиусы равны расстояниям от точек до оси (рис.1). Точки А и В удерживаются неподвижными с помощью подпятника и подшипника соответственно.
Выберем положительное направление оси z и проведем через нее неподвижную плоскость I, вторую плоскость II также проведем через ось и свяжем ее с телом. При вращении плоскость II будет образовывать угол с плоскостью I. Линейный угол ϕ этого движущегося угла называется углом поворота. Если функция ϕ = f (t) известна, то вращательное движение считается заданным. Величина, характеризующая быстроту изменения угла поворота, называется угловой скоростью. Угловая скорость ω определяется как производная по времени от угла поворота
ω= ddtϕ =ϕ& (рад/сек) или (с-1)
Принято считать, что угловая скорость положительна, если в данный момент времени вращение с конца оси представляется происходящим против хода часовой стрелки.
Величина, характеризующая быстроту изменения угловой скорости, называется угловым ускорением, которое определяется как вторая производная от угла поворота по времени или первая производная от угловой скорости
ε= |
d2 ϕ |
= |
dω |
или |
|
|
|||
|
dt 2 dt |
|
||

5
ε=ϕ&&=ω& (рад/сек2) или (с-2)
Если первая и вторая производная от угла ϕ по времени имеют одинаковый знак, то вращение ускоренное, если разный знак – то замедленное. Если угловая скорость постоянна, то вращение равномерное (при этом угловое ускорение ε=0).
2.2.2. Скорость и ускорение точки вращающегося тела
Скорость движения точки тела по окружности называется вращательной скоростью, и модуль ее зависит от расстояния от точки до оси вращения.
V = ω ОМ
Вектор скорости направлен перпендикулярно радиусу окружности, описываемой точкой, в сторону вращения (рис.2).
Ускорение точки вращающегося тела имеет две составляющие – центростремительное и вращательное ускорения.
Ацс = ω2ОМ авр = ε ОМ
Вектор a цс направлен от точки к оси вращения, вектор a вр направлен перпендикулярно радиусу в сторону ε.
Вектор полного ускорения a равен геометрической сумме a цс и a вр
a = a цс + a вр ,
а модуль полного ускорения определится по формуле
а= ОМ  ω4 +ε2
ω4 +ε2
2.2.3.Векторное выражение скорости, центростремительного и вращательного ускорений точек вращающегося тела
Принято считать, что угловая скорость и угловое ускорение – это векторы, направленные по оси вращения, причем вектор ω направлен по оси таким образом, чтобы с его конца вращение представлялось происходящим против хода часовой стрелки, вектор углового ускорения ε также направлен по оси в ту же сторону, что и ω при ускоренном вращении, либо в противоположную – при замедленном.
Вращательная скорость точки, центростремительное и вращательное ускорения могут быть представлены в виде векторных произведений (рис.3).
v =ω x r ,
a цс = ω x v = ω x ω x r
a вр = ε x r
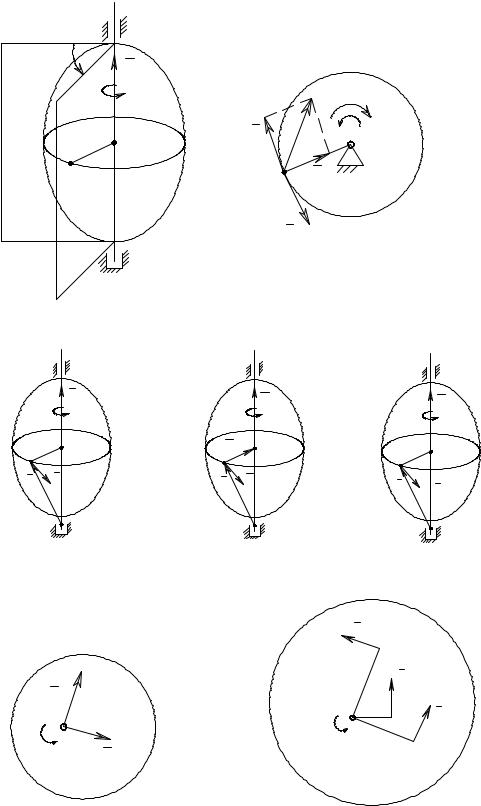
z
В
I j |
w |
|
|
|
w |
|
О |
|
М |
II А
Рис. 1
аz
w w
О
Мr v
6
|
а |
|
авр |
w |
e |
О |
Мацс
v
Рис. 2
б |
z |
в |
z |
|
w |
|
e |
|
w |
|
e |
а |
О |
|
О |
цс |
|
|
|
Мr |
v |
Мr |
а |
|
|
|
вр |
Рис. 3
|
vM |
М |
|
М |
|
vA |
|
rMA |
P |
|
|
A |
A vB |
||
w |
|||
w |
B |
||
v |
|||
|
A |
|
Рис. 4
Рис. 5
