4. Направление выпуклости и точки перегиба кривой

Определение. Кривая называетсявыпуклой (вогнутой) в промежутке , если она лежит ниже (выше) касательной в любой точке этого промежутка.

Выпуклость и вогнутость кривой, являющейся графиком функции , характеризуется знаком её второй производной: если в некотором промежутке, то кривая вогнута в этом промежутке; если же, то кривая выпукла в этомпромежутке.

Определение. Точка графика функции , разделяющая промежутки выпуклости и вогнутости этого графика, называется точкой перегиба.

Точками перегиба могут служить только критические точки, принадлежащие области определения функции у = f(x), в которых вторая производная обращается в нуль или не существует.

Если при переходе через критическую точку вторая производная меняет знак, то график функции имеет точку перегиба (см. рис. 8)

Рис. 8

5. Асимптоты кривой

Определение. Прямая линия называется асимптотой для кривой , если расстояние от точки , лежащей на кривой, до прямой стремится к нулю при удалении точки от начала координат в бесконечность.

Существует три вида асимптот:

1) вертикальные асимптоты

Прямая называется вертикальной асимптотой графика функции ,если хотя бы одно из предельных значений илиравноили.

2) горизонтальные асимптоты

Если , то прямаяназывается горизонтальной асимптотой.

3) наклонные асимптоты

Если существуют такие числа k и b, что и,

прямая называется наклонной асимптотой.

6. Построение графиков функций

Общая схема построения графиков функций:

1) Найти область определения.

2) Выяснить, не является ли функция четной, нечетной или периодической.

3) Найти точки пересечения с осями координат (если это не вызывает затруднений).

4) Исследовать функцию на непрерывность. Найти точки разрыва (если они существуют) и установить характер разрыва. Найти асимптоты графика функции. Выяснить поведение функции в бесконечности.

5) Найти промежутки монотонности функции и её экстремумы.

6) Найти промежутки выпуклости и вогнутости графика функции, точки перегиба.

7) Построить график исследуемой функции.

Пример

Определить интервалы монотонности функции f(x) = x² – 6x + 8.

Решение:

Найдем производную функции .

Точка х = 3 , при которой производная обращается в ноль, разбивает числовую ось на два интервала монотонности (–  , 3) и (3 , +).

Возьмем какую-либо точку, например, х = 0 из первого интервала, в ней . Следовательно, на интервале (–  , 3) функция убывает.

Возьмем какую-либо точку, например, х = 4 принадлежащую второму интервалу, и так как , то на нем функция возрастает.

Пример

Определить точки экстремума функции:

а) f(x) = x³ – 3x + 2 б)

Решение:

а) Находим .

Точки х₁ = –1 и х₂ = +1 – являются критическими, так как в них производная обращается в ноль, Исследуем характер этих точек с помощью достаточного условия. Для этого составим таблицу:

x	(–,–1)	x = –1	(–1, 1)	x = 1	(1, +)
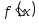
	+	0	–	0	+
f(x)		максимум f(x1) = 4		минимум f(x2) = 0

б) Находим

Критические точки x₁ = 0 (в ней производная не существует) и х = 2

(в ней производная обращается в ноль). Составим таблицу:

x	(–, 0)	x = 0	(0, 2)	x = 2	(2, )
	+	не сущ.	–	0	+
f(x)		максимум f(0) = 0		минимум

Пример

Определить точки перегиба и интервалы выпуклости и вогнутости кривой .

Решение:

Функция определена и дважды дифференцируема для всех х. Точками перегиба могут служить только критические точки, принадлежащие области определения функции у = f(x), в которых вторая производная обращается в ноль или не существует, поэтому найдем .

Разложим на множители и приравняем к нулю:

=0.

Точки x₁ = 0; x₂ = 1; x₃ = 3 – являются критическими точками II рода. Составим таблицу знаков :

x	–  < x < 0	x1 = 0	0 < x < 1	x2 = 1	1 < x < 3	x = 3	3 < x < 
	+	0	+	0	–	0	+
f(x)				ТП		ТП

На первом интервале, например возьмем x = –1, имеем = 240 > 0. Значит, на интервале (–  ,0) функция вогнута. При переходе через точку x₁ = 0 вторая производная знак не меняет, поэтому точка x₁ = 0 не является точкой перегиба. При переходе через точки x₂ = 1; x₃ = 3 вторая производная меняет знак. Эти точки являются точками перегиба.

Найдем значения функции в данных точках:

;

.

На интервалах –  < x < 0, 0 < x < 1 и 3 < x <  кривая выпукла. На интервале 1 < x < 3 кривая вогнута.

Пример

Исследовать функцию и построить ее график.

Решение:

1.Областью определения функции являются все действительные значения аргумента х, то есть .

2. Установим, является ли данная функция четной или нечетной.

Функцияи, следовательно, функция есть функция общего вида.

3. Так как функция непрерывна на всей числовой прямой, то ее график не имеет вертикальных асимптот.

Выясним наличие у графика заданной функции наклонных асимптот. Для определения уравнения наклонной асимптоты воспользуемся формулами:и.

Тогда .

Таким образом, у графика заданной функции наклонных асимптот нет.

4. Определим интервалы возрастания и убывания функции и точки экстремума.

Для исследования функции на экстремум найдем ее первую производную:

.

Найдем критические точки, в которых производная обращается в ноль или не существует. Для этого приравняем производную функции к нулю. Решая данное уравнение, получаем две стационарные точки и .

Разобьем числовую ось найденными критическими точками на интервалы:,,. В первоми третьеминтервалах первая производная положительна, следовательно, здесь функция возрастает; во втором интервалепервая производная отрицательна и данная функция убывает. При переходе через точкупервая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум. Значение функции в точке максимума. Значит,– точка максимума.

При переходе через точку первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум. Значение функции в точке минимума. Значит,– точка минимума.

Знак

5. Найдем интервалы выпуклости и вогнутости кривой и точки перегиба.

Для определения точек перегиба графика функции найдем вторую производную:

Найдем критические точки, в которых производная обращается в ноль или не существует. Для этого приравняем производную к нулю. Решая данное уравнение, получаем .

Р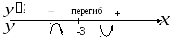азобьем область определения полученной точкой на два интервала,,. В первом интервалевторая производная отрицательна, следовательно, здесь функция выпукла; во втором интервалевторая производная положительна и данная функция вогнута. При переходе через критическую точкувторая производная меняет свой знак, поэтомуабсцисса точки перегиба. Значение функции в точке перегиба. Значит,– точка перегиба графика функции.

Знак

Построим график исследуемой функции.

Пример

Исследовать функцию и построить ее график.

Решение:

1. Область определения функции.

Функция определена при всех значениях аргумента х.

2. Установим, является ли данная функция четной или нечетной

.

Следовательно, данная функция является нечетной, то есть симметрична относительно начала координат.

3. Найдем асимптоты кривой.

А) Исходная функция непрерывна, следовательно, вертикальных асимптот нет.

Б) Найдем наклонные асимптоты.

Для определения уравнения наклонной асимптоты воспользуемся формулами:и.

Тогда .

.

Значит, прямая есть горизонтальная асимптота графика исследуемой функции.

4. Интервалы возрастания и убывания функции и точки экстремума.

Для исследования функции на экстремум найдем ее первую производную:

.

Найдем критические точки, в которых производная обращается в ноль и не существует. Для этого приравняем числитель к нулю. Решая данное уравнение, получаем две стационарные точкии.

Приравняем знаменатель к нулю , то есть. Данное уравнение решений не имеет.

Разобьем числовую ось найденными критическими точками на три интервала: ,,. В первоми третьеминтервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервалепервая производная положительна и данная функция возрастает. При переходе через точкупервая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум. Значение функции в точке минимума. Значит,– точка минимума.

При переходе через точку первая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум. Значение функции в точке максимума. Значит,– точка максимума.

5. Найдем интервалы выпуклости и вогнутости кривой и точки перегиба.

Для определения точек перегиба графика функции найдем вторую производную:

=

Найдем критические точки, в которых производная обращается в ноль и не существует. Для этого приравняем числитель к нулю. Решая данное уравнение, получаем,x = 0,.

Приравняем знаменатель к нулю , то есть. Данное уравнение решений не имеет.

Разобьем числовую ось найденными стационарными точками на четыре интервала: ,,. В первоми третьеминтервалах вторая производная отрицательна, следовательно, здесь функция выпукла; во второми четвертоминтервалах вторая производная положительна и данная функция вогнута. При переходе через стационарные точки,,вторая производная меняет свой знак, поэтому,,– абсциссы точек перегиба. Значение функции в точках перегиба,,. Значит,,,– точки перегиба графика функции.

Построим график исследуемой функции.

.

Пример

Найти наименьшее и наибольшее значение функции f(x) = x³ – 3x² + 1 на отрезке [–1; 4] .

Решение:

1) Найдем критические точки, принадлежащие заданному промежутку [–1; 4], и вычислим значения функции в этих точках. Для этого вычислим производную функции f’(x) = 3x² – 6x = 3x(x – 2).

Для нахождения критических точек приравниваем полученную производную к нулю 3x(x – 2)= 0, тогда x₁ = 0, x₂ = 2 – критические точки. Обе точки принадлежат промежутку [–1; 4] , поэтому находим значение функции в обеих точках

f(0) = 1; f(2) = – 3.

2) Вычислим значения функции на концах промежутка: f(–1) = –3; f(4) = 17

3) Сравнивая полученные значения, имеем:

Наибольшее значение на промежутке– 1 x 4 функция принимает в правом конце отрезка при х = 4.

Наименьшее значение достигается в двух точках: в точке минимума функции и в левом конце интервала прих = –1