
- •§ 2. Геометрический смысл производной
- •§ 3. Физический смысл производной
- •§ 4. Правила дифференцирования
- •§ 5. Таблица производных основных элементарных функций
- •§ 6. Производная сложной функции
- •§ 7. Дифференциал
- •§ 8. Геометрический смысл дифференциала
- •§ 9. Приложения производной
- •1. Возрастание и убывание функции
- •2. Точки экстремума
- •3. Наименьшее и наибольшее значения функции
- •4. Направление выпуклости и точки перегиба кривой
- •5. Асимптоты кривой
- •6. Построение графиков функций
- •Глава 6. Интегральное исчисление функции одной переменной
- •§ 1. Первообразная. Неопределённый интеграл
§ 4. Правила дифференцирования
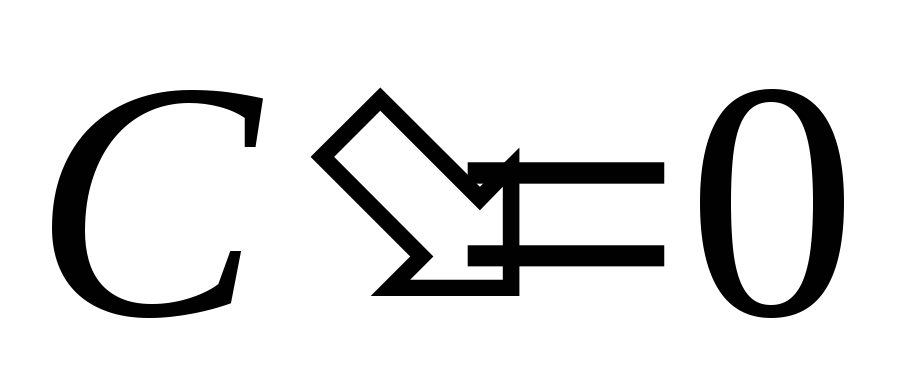 ,
где С
– произвольная постоянная
,
где С
– произвольная постоянная 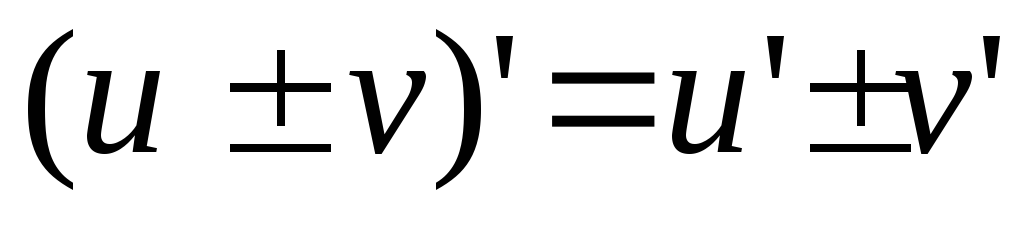 (Производная
алгебраической суммы функций равна
сумме(разности) производных этих же
функций)
(Производная
алгебраической суммы функций равна
сумме(разности) производных этих же
функций)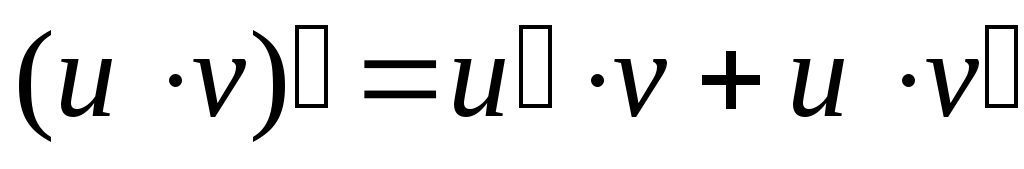
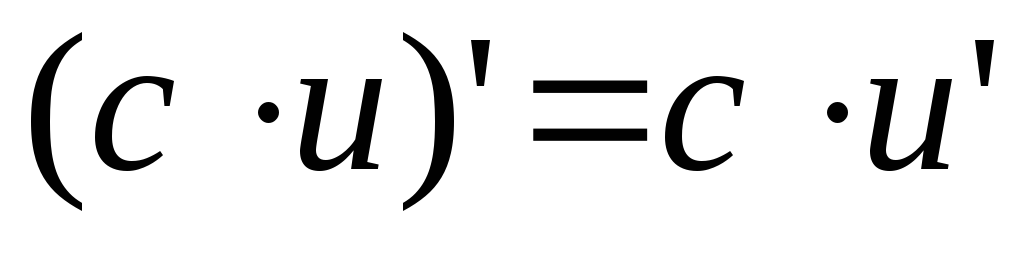 (Постоянная
выносится за знак дифференцирования)
(Постоянная
выносится за знак дифференцирования)
5)
![]()
§ 5. Таблица производных основных элементарных функций
|
|
Производные
от функции
|
Производные
от сложной функции
|
|
1. |
| |
|
Степенная функция | ||
|
2. |
|
|
|
Показательная функция | ||
|
3. |
|
|
|
4. |
|
|
|
Логарифмическая функция | ||
|
5. |
|
|
|
6. |
|
|
|
Тригонометрические функции | ||
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
Обратные тригонометрические функции | ||
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
При дифференцировании степенной функции необходимо помнить:
1)
![]() ,
например,
,
например,![]()
2)
![]() ,
например,
,
например,![]()
3)
![]() ,
например,
,
например,![]()
4)
![]() ,
например,
,
например,![]()
Примеры
1.
Найти производную функции
![]() .
.
Решение:
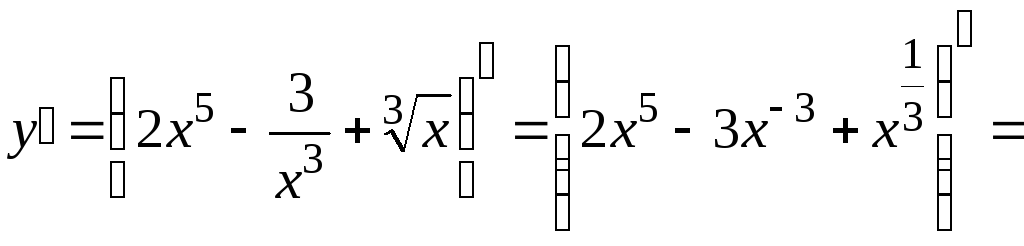
![]()
![]()
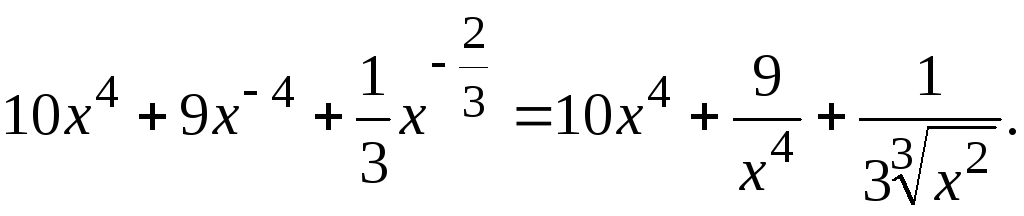
2.
Найти
производную функции
![]() .
.
Решение:
![]()
![]()
3.
Найти
производную функции
![]() .
.
Решение:
![]()
=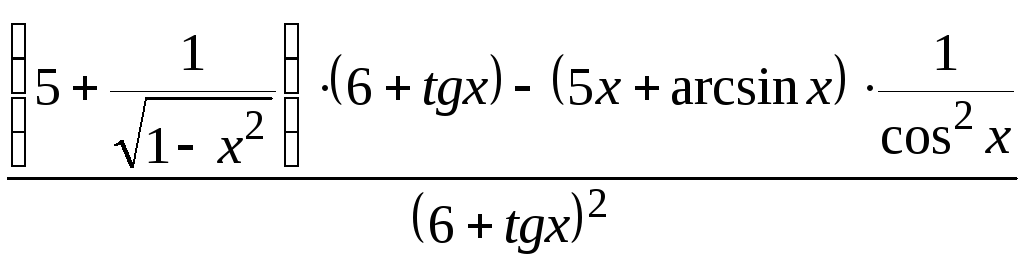
§ 6. Производная сложной функции
Выражение
вида
![]() ,
гдеf,
g
– произвольные функции называется
сложной
функцией.
Иногда функцию f
называют
внешней функцией, а функцию g
– внутренней.
,
гдеf,
g
– произвольные функции называется
сложной
функцией.
Иногда функцию f
называют
внешней функцией, а функцию g
– внутренней.
Правило вычисления производной сложной функции:
![]() .
.
Иными словами, чтобы вычислить производную от сложной функции, необходимо производную от внешней функции f по переменной g умножить на производную от внутренней функции g по переменной х. Необходимо помнить, что при нахождении производной аргумент функции не меняется.
Примеры
1.
Найти
производную функции
![]()
Решение:
![]() .
.
2.
Найти
производную функции
![]() .
.
Решение:
![]() .
.
§ 7. Дифференциал
Определение
1. Главная
линейная часть приращения функции
![]() называетсядифференциалом
функции
называетсядифференциалом
функции
![]() и обозначается df. При этом входящее в
дифференциал приращение независимой
переменной
и обозначается df. При этом входящее в
дифференциал приращение независимой
переменной![]() называется дифференциалом независимой
переменной и обозначается
называется дифференциалом независимой
переменной и обозначается![]() .
.
Таким образом,
![]() .
.
Пример
Найти
дифференциал функции
![]() .
.
Решение:
Найдем
производную от заданной функции:
![]()
Отсюда,
по определению дифференциала
![]() .
.
Формула приближенного вычисления значения функции:
![]() ,
откуда
,
откуда
![]()
Пример
1)
Вычислить
приближенно
![]()
Решение:
Воспользуемся формулой приближенного вычисления
![]()
Исходное
выражение может быть выражено через
функцию
![]() .
.
В
качестве
![]() возьмем число, наиболее близкое к 17, но
чтобы был известен
возьмем число, наиболее близкое к 17, но
чтобы был известен![]() ,
при этом
,
при этом![]() должно быть достаточно малым. Очевидно,
следует взять
должно быть достаточно малым. Очевидно,
следует взять![]() .
Тогда так как
.
Тогда так как![]() ,то
,то![]() .
Найдем значение исходной функции и
значение производной при
.
Найдем значение исходной функции и
значение производной при![]() ,
получим
,
получим![]() .
Теперь найдем производную данной функции
.
Теперь найдем производную данной функции
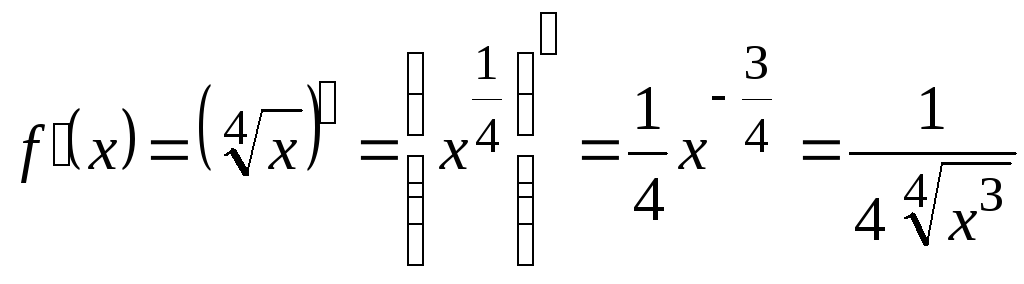
и
ее значение при
![]() ,
то есть
,
то есть![]() .
.
Подставляя
найденные значения в формулу
![]() ,
получим
,
получим
![]() .
.
2)
Вычислить
приближенно
![]()
Решение:
Полагая
![]() ,
найдем
,
найдем![]() .
Так как
.
Так как![]() радиан, то возьмем
радиан, то возьмем![]() при этом значении
при этом значении
![]() и
и
 .
Так как
.
Так как![]() ,
то
,
то![]() .
Подставляя найденные значения в формулу
.
Подставляя найденные значения в формулу![]() ,
получим
,
получим
![]() .
.
Пример
Формулу
![]() принято использовать в приближенных
вычислениях при оценке погрешностей,
в частности, при определении твердости
металлов. При определении твердости по
Виккерсу измерения показали, что
диагональ отпечатка равна 3,76 мм, причем
максимально возможная при этом погрешность
измерения находится в пределах ±0,01 мм.
Оцените относительную погрешность,
допускаемую при вычислении числа
твердости.
принято использовать в приближенных
вычислениях при оценке погрешностей,
в частности, при определении твердости
металлов. При определении твердости по
Виккерсу измерения показали, что
диагональ отпечатка равна 3,76 мм, причем
максимально возможная при этом погрешность
измерения находится в пределах ±0,01 мм.
Оцените относительную погрешность,
допускаемую при вычислении числа
твердости.
Решение:
Имеем
функцию
![]() ,
гдеk
– величина, не зависящая от x
,
,
гдеk
– величина, не зависящая от x
,
![]() ,
,![]() .
Поэтому
.
Поэтому![]() ,
,![]() ,
или применительно к конкретным данным
,
или применительно к конкретным данным![]() ,
т.е. относительная погрешность будет
около 0,53%.
,
т.е. относительная погрешность будет
около 0,53%.
Пример
Автомобиль, проходящий поворот, занимает на проезжей части большую ширину, чем на прямолинейном участке дороги. Найдите необходимое уширение однополосной дороги на повороте радиуса r (r – радиус внешнего края дороги) для автомобиля, продольная база (расстояние между осями) которого равна l.
Решение:
На
повороте все четыре колеса автомобиля
катятся по дугам концентрических
окружностей, причем заднее внутреннее
колесо D
описывает окружность наименьшего, а
переднее наружное В
– наибольшего радиуса. Поэтому ширина
дорожной полосы на повороте h
= OB – OD, а
искомое уширение
![]() .
Величина
.
Величина![]() довольно мала при больших
довольно мала при больших![]() .
Поэтому для вычисления значения
.
Поэтому для вычисления значения![]() можно воспользоваться формулой
можно воспользоваться формулой![]() ,
где
,
где![]() ,
,![]() ,
,![]() ;
;![]() .
Получим формулу
.
Получим формулу![]() ,
которая используется на практике.
,
которая используется на практике.
