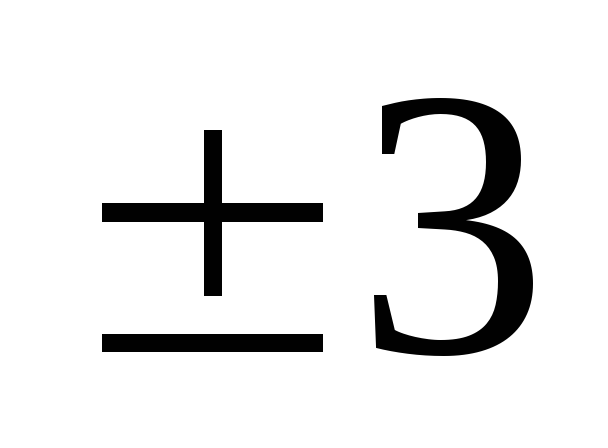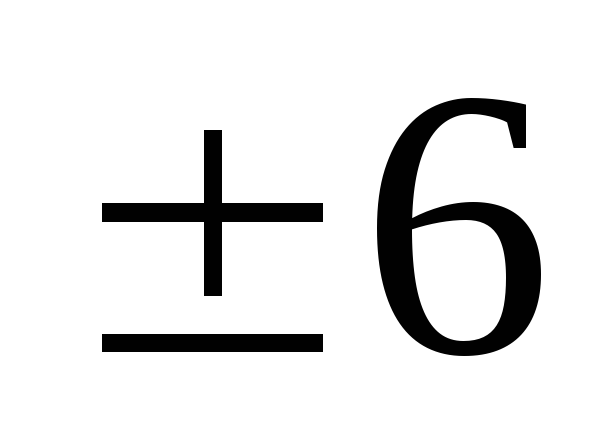7_54-63

Выделяют четыре основных типа кривых второго порядка: окружность, эллипс, гипербола и парабола.

1. Окружность

Определение. Окружностью называется множество, состоящее из всех точек плоскости, находящихся на равном расстоянии R от фиксированной точки С.

Число R называется радиусом окружности, точка С – центром.

Воспользуемся определением окружности для вывода ее уравнения.

П

Рис. 5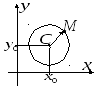

усть точка – центр окружности. Точка – произвольная точка окружности, а радиус этой окружности равен . По определению , тогда, используя формулу вычисления длины вектора , имеем , тогда

. Возведем обе части равенства в квадрат. Тогда уравнение окружности с центром в точке и радиусом R имеет вид:

каноническое уравнение окружности

В частности, уравнение окружности с центром в начале координат и радиусом R имеет вид: .

Пример

Составить каноническое уравнение окружности, центр которой находится в точке , а диаметр .

Решение:

Найдем радиус , тогда уравнение окружности имеет вид

или .

Пример

Построить окружность по заданному уравнению . Привести каноническое уравнение к общему виду.

Решение:

П

Рис. 6

о заданному уравнению определяем, что центр окружности , а радиус . Теперь преобразуем каноническое уравнение к общему виду или , полученное уравнение является общим уравнением окружности с центром в точке и радиусом .

Возможно решение обратной задачи: общее уравнение преобразовать в каноническое.

2. Эллипс

Определение 1. Эллипсом называется множество, состоящее из всех точек плоскости, сумма расстояний от каждой из которых до двух заданных точек плоскости и , называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

В случае, когда фокусы эллипса и расположены на оси Ox (или на оси Oy) симметрично относительно начала координат, его уравнение называется каноническим и имеет вид:

.

Обозначим через 2с расстояние между фокусами эллипса. Если a > b (a < b), то фокусы эллипса расположены на оси Ox (на оси Oy) и (cм. рис. 7). Фокусы эллипса всегда лежат на большей оси. Отрезки ОА и ОВ называются полуосями эллипса. Точки пересечения линии эллипса с осями координат А, В, А₁, В₁ называются вершинами эллипса. Эллипс имеет две оси симметрии (в случае, если эллипс задается каноническим уравнением, оси симметрии совпадают с осями координат) и центр симметрии (в случае, если эллипс задается каноническим уравнением, центр симметрии совпадает с началом координат).

Рис. 7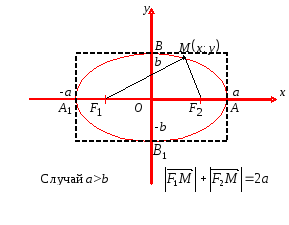

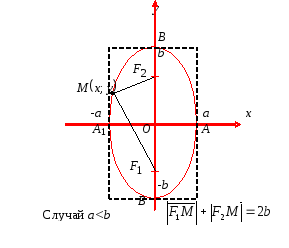
Для количественной оценки формы эллипса введена величина, называемая эксцентриситетом эллипса.

Определение 2. Эксцентриситетом эллипса называется величина, равная отношению расстояния между фокусами к длине его большей оси.

Обозначим эксцентриситет эллипса через . Пусть a > b (a < b). Тогда (). Так как 0 < с < a (0 < с < b) , то 0 <  < 1. Чем ближе эксцентриситет к единице, тем эллипс более вытянут вдоль большей оси.

3. Гипербола

Определение 1. Гиперболой называется множество, состоящее из всех точек плоскости, модуль разности расстояний от которых до двух фиксированных точек и , называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами, и отличная от нуля.

Каноническое уравнение гиперболы имеет вид:

(1)

(в случае, если фокусы и расположены на оси Ох симметрично относительно начала координат, см. рис. 8) или

(2)

(в случае, если фокусы и расположены на оси Оу симметрично относительно начала координат, см. рис. 9).

Гиперболы, заданные уравнениями (1) и (2), называются сопряженными относительно друг друга.

Обозначим через 2с расстояние между фокусами гиперболы. Тогда .

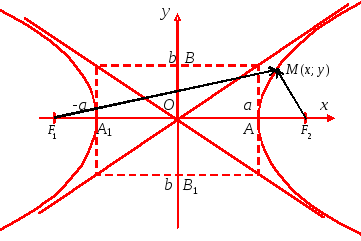
Рис. 8 Рис. 9

Точки А и А₁ – вершины гиперболы. Точки В и В₁ – вершины гиперболы.

Прямоугольник, составленный прямыми , называется основным прямоугольником гиперболы. Его диагонали совпадают с прямыми , которые являются асимптотами гиперболы. Отрезки ОА = a и OB = b называются полуосями гиперболы. Ось координат, на которой расположены фокусы гиперболы (и которую пересекает гипербола) называется действительной, другая ось координат (с которой у гиперболы нет общих точек) – мнимой.

Гипербола называется равносторонней, если длины осей равны .

Форму гиперболы определяет отношение длин основного прямоугольника. Для количественной оценки формы гиперболы, как и в случае эллипса, вводится понятие эксцентриситета.

Определение 2. Эксцентриситетом гиперболы называется величина, равная отношению половины расстояния между фокусами к длине действительной полуоси.

Обозначим эксцентриситет гиперболы через . Для гиперболы, заданной уравнением (1), ; для гиперболы, заданной уравнением (2) . Так как 0 < а < с и 0 < b < с, то  > 1. Чем ближе эксцентриситет к единице, тем основной прямоугольник гиперболы более вытянут вдоль ее оси, соединяющей вершины.

4. Парабола

Определение. Параболой называется множество, состоящее из всех точек на плоскости, для которых расстояние до некоторой фиксированной точки F, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.

На рисунках 10–13 представлены все простейшие случаи расположения параболы и соответствующие им канонические уравнения.

p – параметр, он равен расстоянию между фокусом и директрисой;

точка F – фокус.

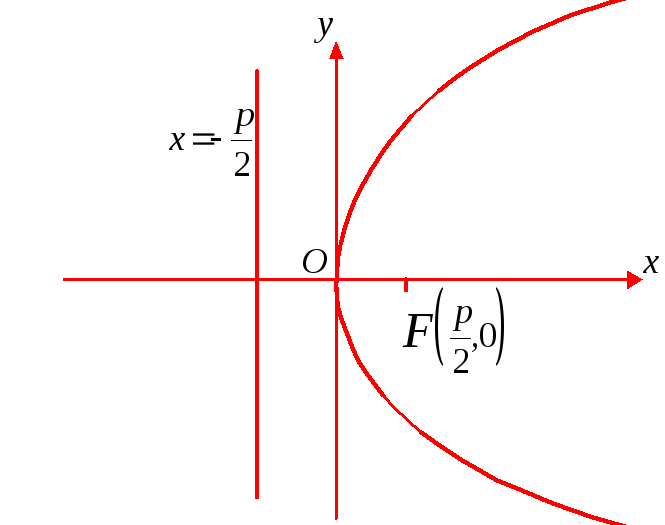
Рис. 10 Рис. 11

На рис. 10 парабола ; уравнение директрисы .

На рис. 11 парабола ; уравнение директрисы .

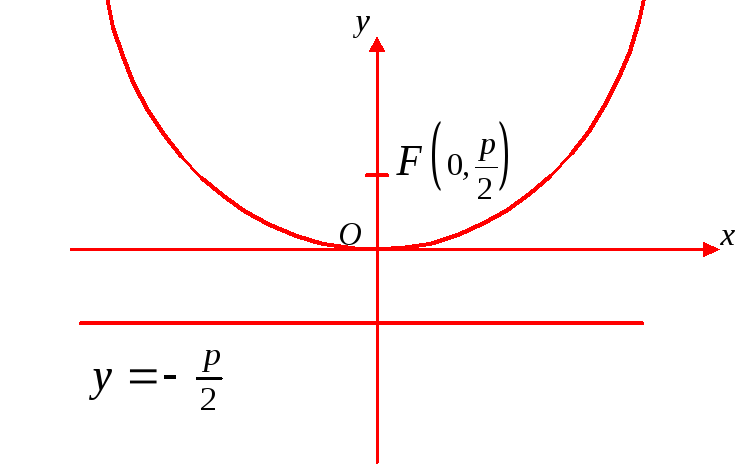
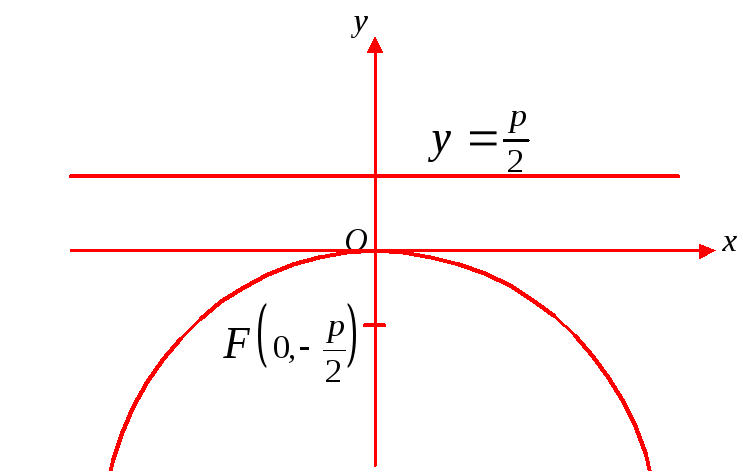
Рис. 12 Рис. 13

На рис. 12 парабола ; уравнение директрисы .

На рис. 13 парабола ; уравнение директрисы .

Пример

По заданному каноническому уравнению построить кривую, найти координаты фокусов.

Решение:

З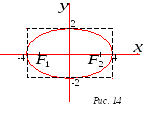аданное уравнение есть уравнение эллипса, где , , следовательно, , , тогда .

На оси отметим точки и , а на оси отметим и это вершины эллипса.

Соединим полученные точки плавной линией. Прямоугольных участков быть не должно. Эллипс – это сжатая окружность.

Найдем фокусы эллипса, так как , то фокусы располагаются на оси и имеют координаты и .

Пример

Общее уравнение кривой привести к каноническому виду, построить кривую, найти координаты фокусов.

Р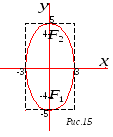ешение:

Перенесем свободный член вправо . Разделим слагаемое уравнения на 225, получим , это уравнение соответствует каноническому уравнению эллипса, где , , следовательно, , , тогда .

На оси отметим точки и , а на оси отметим и – это вершины эллипса.

Найдем фокусы эллипса, так как , то фокусы располагаются на оси и имеют координаты и .

Пример

Дано каноническое уравнение гиперболы . Записать уравнение гиперболы, сопряженной с заданной. Найти координаты фокусов и построить обе гиперболы.

Решение:

Уравнение соответствует гиперболе, у которой действительная ось симметрии есть ось . Следовательно, уравнение сопряженной гиперболы , у которой действительная ось симметрии есть ось . Межфокусное расстояние у сопряженных гипербол одинаковое, равно , где .

Подготовка к построению сопряженных гипербол одинаковая. На осях координат строим основной прямоугольник со сторонами и . Прямоугольник строится так, чтобы точка пересечения его диагоналей совпадала с началом координат. Продолжение диагоналей являются асимптотами гиперболы. В нашем случае уравнения асимптот имеют вид: . Для уравнения заданной гиперболы вершины гиперболы и , так же как и фокусы и , находятся на оси . Линия гиперболы касается вспомогательного прямоугольника только в одной точке (вершине) и плавно стремится к асимптотам. Для уравнения сопряженной гиперболы вершины гиперболы и , так же как и фокусы и , находятся на оси .

Рис. 16

Пример

Построить по заданному уравнению параболы , определить координаты фокуса, составить уравнение директрисы.

Решение:

Данное уравнение – это уравнение параболы с осью симметрии . Для нахождения координат фокуса надо найти параметр . Сравнивая каноническое уравнение параболы и заданное уравнение , находим , откуда . Следовательно, и уравнение директрисы , а ветви параболы направлены вверх. Кроме вершины найдем еще хотя бы 4 точки, принадлежащие данной параболе (рис. 17). Для этого составим таблицу

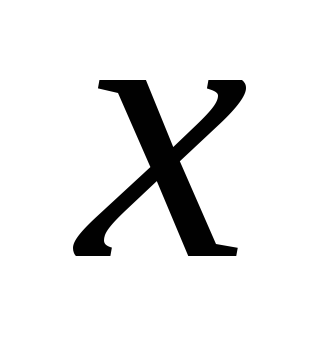
	0
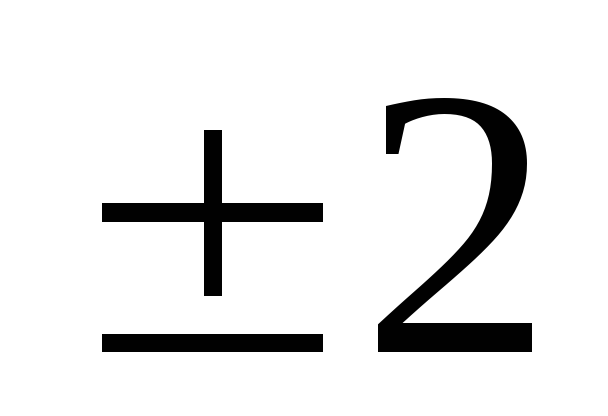
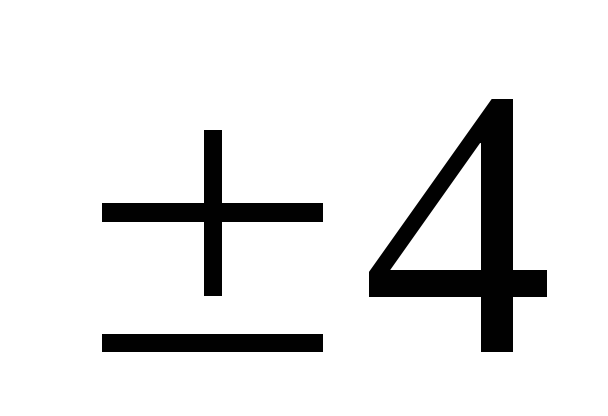
	0	1	4

Пример

Привести уравнение к каноническому виду и выполнить задания предыдущего примера.

Решение:

Преобразуем уравнение к каноническому виду . Это уравнение соответствует уравнению , то есть уравнению параболы с осью симметрии . Аналогично предыдущему примеру находим , откуда . Следовательно, и уравнение директрисы , а ветви параболы направлены влево. Кроме вершины найдем еще хотя бы 4 точки, принадлежащие данной параболе (рис. 18). Для этого составим таблицу

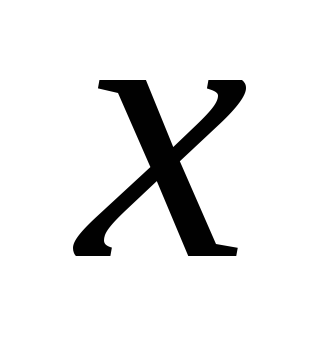
	0	-1,5	-6
	0

62