§ 5. Формула полной вероятности. Вероятности гипотез. Формула Байеса

Пусть имеется некоторый комплекс условий .

Определение 1. Совокупность событий , из которых хотя бы одно происходит в результате комплекса условий, называется полной группой событий.

Предположим, что события , которые могут произойти в результате комплекса условий, образуют полную группу событий и, кроме того, эти события являются попарно несовместными. Пусть A – любое событие, которое может произойти в результате этого же комплекса условий. Тогда вероятность события A может быть вычислена с использованием вероятностей и условных вероятностей .

Теорема 1. Пусть задан некоторый комплекс условий , в результате которого могут произойти события , образующие полную группу попарно несовместных событий. Тогда вероятность любого события A, которое может произойти в результате того же комплекса условий, вычисляется по формуле (полной вероятности).

Теорема 2 (Байеса). Пусть задан некоторый комплекс условий, в результате которого могут произойти события , образующие полную группу попарно несовместных событий. Пусть в результате комплекса условий уже произошло некоторое событие A. Тогда вероятности гипотез могут быть переоценены по формуле Байеса

().

Пример

Страховая компания разделяет застрахованных по классам риска: I класс – малый риск, II класс – средний, III класс – большой риск. Среди этих клиентов 50% – первого класса риска, 30% – второго и 20% – третьего. Вероятность необходимости выплачивать страховое вознаграждение для первого класса риска равна 0,01, второго – 0,03, третьего – 0,08. Какова вероятность того, что: 1) застрахованный получит денежное вознаграждение за период страхования; 2) получивший денежное вознаграждение застрахованный относится к группе малого риска?

Решение:

1) Событие A – застрахованный получил денежное вознаграждение за период страхования. Гипотезы:

H₁ – застрахованный относится к I классу, ;.

H₂ – застрахованный относится к II классу, ;.

H₃ – застрахованный относится к III классу, ;.

По формуле полной вероятности: .

2) Найдем условную вероятность того, что получивший денежное вознаграждение застрахованный относится к группе малого риска, по формуле Байеса:.

§ 6. Повторные испытания. Формула Бернулли. Теорема Лапласа. Формула Пуассона

Пусть имеется комплекс условий , в результате которого может появиться некоторое событиеA, вероятность которого равна . Рассмотрим новый комплекс условий , который заключается в том, что исходный комплекс условийповторяется раз. В такой ситуации говорят, что имеется схема повторных испытаний Бернулли. Рассмотрим событие , которое заключается в том, что при осуществлении комплекса условий , то есть в результате испытаний, событие появится ровно раз. Положим и найдем формулы для вычисления вероятности .

Формула Бернулли. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна , где .

Вероятность того, что в независимых испытаниях событие наступит:

1) менее раз ;

2) более раз ;

3) не менее раз ;

4) не более раз .

Локальная теорема Муавра-Лапласа. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше )

,

Обычно формулу Муавра-Лапласа применяют при и (число испытаний велико, а значения вероятности не слишком близки к нулю или к единице). В таблице 1 даны значения функции Гаусса для некоторых значений . Для отрицательных значений числовые значения функции Гаусса находятся из условия ее четности: .

Интегральная теорема Муавра-Лапласа. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит не менее раз и не более , приближенно равна (тем точнее, чем больше )

.

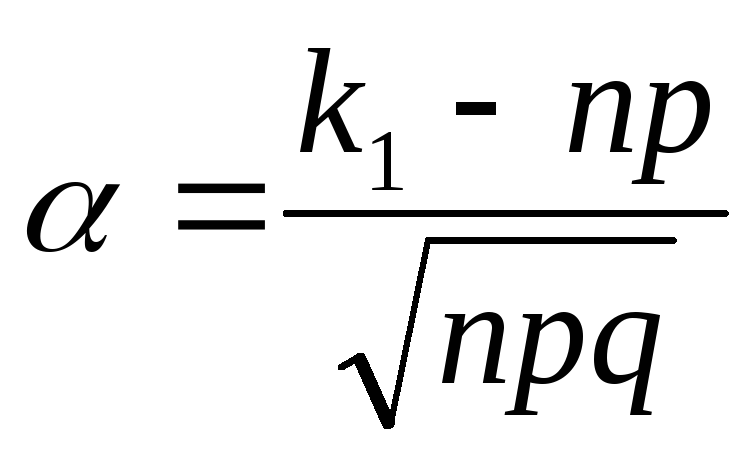Здесь – функция Лапласа, и .

Таблица функции Лапласа для положительных значений х () приведена в приложении 2. Для значенийполагают . Для отрицательных значений х учитывают, что функция Лапласа нечетная .

Формула Пуассона

Формулу используют для приближенного вычисления вероятности того, что событие A наступит ровно раз в серии из испытаний, в том случае, когда число достаточно велико, а вероятность события достаточно мала () полагают, что , где .

Пример

Предполагается, что 40% деревьев в лесопарковой зоне могут быть повреждены болезнью. Найти вероятность того, что из шести выбранных для проверки деревьев будут повреждены: а) ровно четыре; б) не более четырех.

Решение:

а) Очевидно, имеет место формула Бернулли, где,,,, поэтому

.

б) Можно решать двумя способами:

1 способ:

=++++=

2 способ: .

Во втором случае вычисления проще, и это полезно учитывать при решении задач.

Пример

При пересадке саженцев голубой ели выживает 80% саженцев. Определить вероятность того, что из 100 пересаженных саженцев, выживет: 1) ровно 75; 2) не менее 75; 3) не более 75.

Решение:

Поскольку велико,,не малы, применим приближенные формулы:

1) локальную теорему Лапласа , гдефункция четная и. В нашем случае.

Тогда (находим по таблице приложение 1)

.

2) интегральную теорему Лапласа:

Если вероятность наступления события в каждом изнезависимых испытаний постоянна и равна, то вероятностьтого, что событиев таких испытаниях наступит не менеераз и не болеераз, вычисляется по формуле:,

где ,.

В приложении 2 даны значения этой функции для . Прифункция.

В нашей задаче и. Тогда

3) интегральную теорему Лапласа:

и

Пример

В питомнике выращивали 1000 саженцев липы. Вероятность того, что среди них окажутся саженцы другой породы, равна 0,003. Найти вероятность того, что таких саженцев окажется: 1) ровно два; 2) хотя бы один.

Решение:

Число велико, вероятностьмала и рассматриваемые события независимы, поэтому имеет место формула Пуассона , где , то есть .

1. Найдем вероятность того, что среди 1000 ровно два саженца другой породы: .

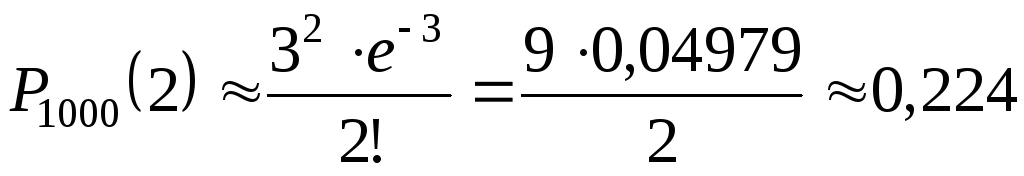2. Событие – хотя бы один саженец другой породы. Противоположным событием к событию «хотя бы один» является событие «ни одного», следовательно,

.