Статистика _Овсянникова (исправленный)

по специальности – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Решение. Параметры теоретического нормального закона распределения a и σ 2 , являющиеся соответственно математическим ожиданием и дисперсией случайной величины X, неизвестны, поэтому заменяем их «наилучшими» оценками по выборке – несмещенными и состоятельными оценками соответственно выборочной средней xB и «исправленной» выборочной дисперсией S 2 . Так как число наблюдений n =100 достаточно велико, то вместо исправленной S 2 можно взять «обычную» выборочную дисперсию σB2 . В задании 2 а1 было найдено a = xB =10,12 ; σ =σB2 =19,07 . Тогда

σ = σB2 = 19,07 = 4,37 .

Так как случайная величина имеет нормальное распределение, то для расчета вероятностей попадания случайной величины X в интервал [xi ; xi+1 ], где i =1, 2,K, m , используем функцию Лапласа в соответствии со свойствами нормального распределения:

ется при нахождении вероятностей попадания случайной величины X в интервал [xi ; xi+1 ] для всех значений случайной величины X, за исключением крайних значений, то есть x1 и

При нахождении вероятности попадания случайной величины X в интервал [x1; x2 ] полагаем x1 = −∞, то есть искомая вероятность будет определяться следующей формулой:

60

Φ(−x) = −Φ(x) , находим значения функции Лапласа для отрицательных аргументов, используя таблицы приложения 2 в настоящих методических указаниях или в книгах [1] или [5].

При нахождении вероятности попадания случайной величины

Таким образом, в нашем примере получим:

p1 = P(− ∞ ≤ X ≤ 5)= Φ 5 −10,12 − Φ(− ∞)=4,37

= Φ(−1,17)− Φ(− ∞)= −Φ(1,17)+ Φ(∞) = −0,3790 + 0,5 = 0,121,

= Φ(−0,26)−Φ(−1,17)= −Φ(0,26)+Φ(1,17) = −0,1026+0,3790 = 0,2764,

= Φ(0,66)−Φ(−0,26)= Φ(0,66)+Φ(0,26) = 0,2453+0,1026 = 0,3479,

= Φ(∞)−Φ(1,58)= 0,5 −0,4429 = 0,0571.

61

Для определения выборочной статистики (4.6)

где ni′ = n pi – теоретические частоты, составим расчетную табл.4.1.

Таблица 4.1

Из табл. 4.1 находим фактически наблюдаемое значение статистики (выборочная статистика) χ2 = 9,769 .

Так как число интервалов k = 5 , а нормальный закон распределения определяется s = 2 параметрами, точечные оценки которых были получены по выборочным данным, то число степеней

тические точки распределения χ2 » в приложении 3 настоящих методических указаний или в приложении 5 в книгах [1] или [5].

Имеем χкр2 = χ2 (0,05;2) = 6,0 .

Так как 9,769 = χ2 > χкр2 = 6,0 , то гипотеза о выбранном теоретическом нормальном законе распределения с параметрами a =10,12 и σ = 4,37 не согласуется с опытными данными (в данном примере), то есть гипотеза отвергается на заданном уровне значимости α = 0,05 .

62

Изобразить эмпирические распределения можно, например, ступенчатой фигурой, состоящей из прямоугольников с основания-

мой гистограммой. При построении нормальной кривой для каждого интервала по оси ординат откладываем соответствующие вероятности pi (теоретические частоты ni′ = n pi ). Вершина нормальной кри-

приведены в приложении 1 настоящих методических указаний или в приложении 1 в книгах [1] или [5]).

Выполнив чертеж (рис. 4.3), можно увидеть, что нормальная кривая теоретического распределения практически не «выравнивает» гистограмму эмпирического распределения.

Замечание 1. Если при проверке гипотезы используется таблица вероятностей P(χ2 > χкр2 (α, k)), как, например, таблицы, приве-

63

денные в пособиях [3] (приложение 4) , то необходимо найти вероятность Р для вычисленного значения χ2 = 9,769 при числе степеней свободы r = k − s −1 = 2 . Непосредственно такого значения в таблицах нет. Но (при r = 2 ) для ближайших соседних значений χ2 , равных 9 и 10, вероятность Р соответственно равна 0,0111 и 0,0067. Таким образом, и без интерполяции ясно, что вероятность Р меньше заданного уровня значимости α = 0,05 , то есть Р<0,05, следовательно, нулевая гипотеза H0 не согласуется с опытными данными.

Задание 2

Пример 2, г2

Получено следующее распределение 100 рабочих цеха по выработке в отчетном году (в процентах к предыдущему году):

мальном распределении случайной величины X – выработки рабочих – с помощью критерия χ2 Пирсона. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Решение. Параметры теоретического нормального закона распределения a и σ 2 , являющиеся соответственно математическим ожиданием и дисперсией случайной величины X, неизвестны, поэтому заменяем их «наилучшими» оценками по выборке – несмещенными и состоятельными оценками соответственно выборочной средней xB и «исправленной» выборочной дисперсией S 2 . Так как число наблюдений n =100 достаточно велико, то вместо исправленной S 2 можно взять «обычную» выборочную дисперсию σB2 .

64

Найдем выборочную среднюю xB (по упрощенной формуле):

65

Так как случайная величина имеет нормальное распределение, то для расчета вероятностей попадания случайной величины X в интервал [xi ; xi+1 ], где , используем функцию Лапласа в соответствии со свойствами нормального распределения:

Так как нормальное распределение определено на всей числовой оси, то есть x (−∞;∞), то указанная выше формула применяется при нахождении вероятностей попадания случайной величины X в интервал [xi ; xi+1 ] для всех значений случайной величины X, за исключением крайних значений, то есть значений x1 и xm+1 .

Вероятность попадания случайной величины X в интервал [x1; x2 ] определяется следующей формулой

Вероятность попадания случайной величины X в интервал [xm ; xm+1 ] определяется следующей формулой

pm = P(xm ≤ X ≤ xm+1 )= P(xm ≤ X ≤∞)=Φ ∞σ−a −Φ xmσ−a =

Таким образом, в нашем примере получим:

66

= Φ(−1,68)−Φ(−∞)= −Φ(1,68)+ Φ(∞) = −0,4535 + 0,5 = 0,0465;

= Φ(−0,55)−Φ(−1,68)= −Φ(0,55)+Φ(1,68) = −0,2088+0,4535 = 0,2447;

= Φ(0,57)−Φ(−0,55)= Φ(0,57)+Φ(0,55) = 0,2157 +0,2088 = 0,4245;

Запишем в табл. исходные данные и найденные вероятности. Вычислим в табл. теоретические частоты ni′ = n pi .

Таблица 4.3

Так как в последнем (пятом) интервале число наблюдений меньше пяти, то имеет смысл для применения критерия χ2 Пирсона объединить последний интервал с предыдущим (как для эмпирических так и для теоретических частот), полагая при вычислении

67

χ2 эмпирическую частоту, равной 27 + 2 = 29 , теоретическую час-

тоту, равной 23,97 + 4,46 = 28,43 .

Для определения выборочной статистики (4.6)

χ2 = ∑m (ni −′ni′)2 ,

i=1 ni

составим расчетную табл. 4.4.

рых были получены по выборочным данным, то число степеней

тические точки распределения χ2 » в приложении 3 настоящих методических указаний или в приложении 5 в книгах [1] или [5]. Имеем χкр2 = χ2 (0,05;1) = 3,8. Так как 1,373 = χ2 < χкр2 =3,8 , то гипотеза о выбранном теоретическом нормальном законе распределения с параметрами a =118,9 и σ = 8,89 согласуется с опытными данными, то есть гипотеза принимается на заданном уровне значимости

α = 0,05 .

На одном чертеже построим нормальную кривую и гистограмму. Вершина нормальной кривой имеет координаты x = a =10,12 ;

68

Лапласа, значения которой приведены в приложении 1 настоящих методических указаний или в приложении 1 в книгах [1] или [5]).

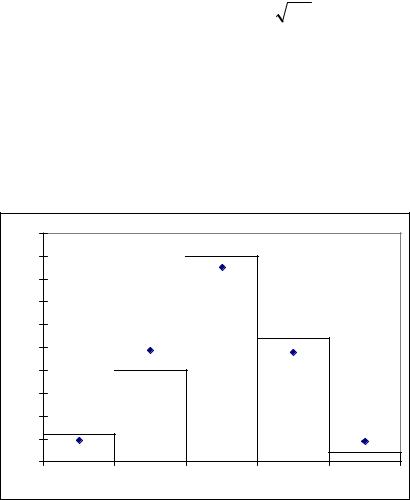
Выполнив чертеж (рис. 4.4), можно увидеть, что нормальная кривая теоретического распределения достаточно хорошо «выравнивает» гистограмму эмпирического распределения.

Рисунок 4.4

Замечание. Если при проверке гипотезы используется таблица вероятностей P(χ2 > χкр2 (α, r)), как, например, таблицы, приведенные в пособии [3] (приложение 4) или в более ранних изданиях [1] и [5], то необходимо найти вероятность Р для вычисленного значения χ2 =1,373 при числе степеней свободы r = k − s −1 =1. Непосредственно такого значения в таблице нет. Но (при r =1) для ближайших соседних значений χ2 , равных 1 и 2, вероятность Р соответственно равна 0,3173 и 0,1574. Таким образом, и без интерполяции ясно, что вероятность Р больше заданного уровня значимости α = 0,05 , то есть Р>0,05, следовательно, нулевая гипотеза H0 согласуется с опытными данными.

69