
Статистика _Овсянникова (исправленный)
.pdf
Накопленные частоты для каждого интервала находятся последовательным суммированием относительных частот всех предшествующих интервалов, включая данный.
Находим выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение для выборки X.
|
|
|
|
~ |
|
|
|
+ 47 12 + 53 17 + 59 27 |
|
|
|
|
||||||
|
|
xB = |
|
∑ xi n i |
|
= 41 2 |
+ |
|
|
|
||||||||
|
|
|
|
n |
|
100 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
+ 65 21 + 71 14 + 77 6 + 83 1 = 60,44 |
|
|
|
|
|
|||||||||||
|
~ |
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
ni |
|
(41 |
− 60,44) |
2 |
2 + (47 − 60,44) |
2 |
12 |
+ (53 |
− 60,44) |
2 |
17 |
|
|||
DB = |
∑(xi − xв ) |
|
= |
|
|
|
+ |
|||||||||||
|
|
n |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
+ (59 − 60,44)2 27 + (65 − 60,44)2 21 +1 + 100
+ (71 − 60,44)2 14 + (77 − 60,44)2 6 + (83 − 60,44)2 =80,7264 100
σB = DB = 80,7264 =8,98
3. Записываем эмпирическую функцию распределения (по значениям столбца накопленных частот табл. 2).
0 |
x ≤ 41 |
|
41 < x ≤ 47 |
0.02 |
|
|
47 < x ≤ 53 |
0.14 |
|
0.31 |
53 < x ≤ 59 |
|
59 < x ≤ 65 |
F*(x) = 0.58 |
|
0,79 |
65 < x ≤ 71 |
|
71 < x ≤ 77 |
0.93 |
|
|
77 < x ≤83 |
0,99 |
|
|
x >83 |
1 |
Строим график эмпирической функциираспределения (рис. 6.1) 4. По интервальному ряду распределения (значения столбца "wx/hx" табл.6.2) строим гистограмму относительных частот для
выборки X (рис.6.2)
90

1,2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
32 |
38 |
44 |
50 |
56 |
62 |
68 |
74 |
80 |
86 |
|
|
|
Рисунок 6.1 |
|
|
|
|
||
0,06 |
|
|
|
|
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
|
|
0,04 |
|
|
|
|
|
|
|
|
|
0,03 |
|
|
|
|
|
|
|
|
|
0,02 |
|
|
|
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
32 |
38 |
44 |
50 |
56 |
62 |
68 |
74 |
80 |
86 |
|
|
|
Рисунок 6.2 |
|
|
|
|
||
По виду гистограммы выдвигается гипотеза о том, что теоретическое распределение является нормальным. С помощью выборочного распределения, оцениваются два параметра нормального распределения: математическое ожидание и среднеквадратическое отклонение σ ≈σB .
Итак, проверяем гипотезу о нормальном законе распределения случайной величины X.
Так как случайная величина имеет нормальное распределение, то для расчета вероятностей попадания случайной величины X в интервал [xi ; xi+1 ], где i =1,2,K, m , используем функцию Лапласа в соответствии со свойствами нормального распределения:
91
|
|
|
|
|
|
|
x |
|
− a |
x |
− a |
||||||
p |
i |
= P(x ≤ X |
≤ x |
)= Φ |
i+1 |
|
|
|
−Φ |
i |
|
= |
|||||
|
|
|
|
|
|
||||||||||||
|
i |
|
i+1 |
|
|
σ |
|
|
|
σ |
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
−10,12 |
|
x |
−10,12 |
|
|
||||||||
|
|
= Φ |
i+1 |
|
|
−Φ |
|
i |
|
|
|
. |
|
|
|||
|
|
|
4,37 |
|
4,37 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Так как нормальное распределение определено на всей число- |
|||||||||||||||||
вой оси, т.е. x (−∞;∞), |
то указанная выше формула применяется |
||||||||||||||||
при нахождении вероятностей попадания случайной величины X в |
|||||||||||||||||
интервал [xi ; xi+1 ] для всех значений случайной величины X, за исключением крайних значений, т.е. x1 и xm+1 .
При нахождении вероятности попадания случайной величины
X в интервал [x1; x2 ], полагаем x1 |
= −∞ , т.е. искомая вероятность бу- |
||||||||||||||||||||
дет определяться следующей формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x |
|
−a |
|
−∞−a |
|
|||||||
p = P(x |
≤ X ≤ x )= P(−∞≤ X ≤ x )=Φ |
|
2 |
|
|
|
−Φ |
|
|
|
= |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
1 |
|
|
2 |
|
2 |
|
|
σ |
|
|
|
|
σ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x |
−a |
x −a |
|
|
|
|
x |
−a |
|
|
|
||||||||||
=Φ |
2 |
|
|
|
−Φ(−∞)=Φ |
2 |
|
+Φ(∞)=Φ |
2 |
|
+0,5. |
|
|||||||||
|
|
|
σ |
|
|
|
|
||||||||||||||
|
σ |
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
||||
В силу нечетности функции Лапласа |
|
Φ(x) , т.е. |
Φ(−x) = −Φ(x) , |
||||||||||||||||||
находим значения функции Лапласа для отрицательных аргументов используя таблицы приложения 1.
При нахождении вероятности попадания случайной величины
X в интервал [xm ; xm+1 ], |
полагаем |
xm+1 = ∞ , т.е. искомая вероятность |
||||||||||||||||
будет определяться следующей формулой |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∞−a |
x |
−a |
|
|||
p |
= P(x ≤ X |
≤ x |
|
)= P(x ≤ X ≤∞)=Φ |
|
|
−Φ |
m |
|
|
= |
|||||||
|
|
|
|
|||||||||||||||
m |
m |
|
|
m+1 |
|
m |
|
|
|
σ |
|
σ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
−a |
|
|
x |
|
−a |
|
|
|
|
|
|
|
||||
=Φ(∞)−Φ |
m |
|
|
=0,5 |
−Φ |
m |
|
. |
|
|
|
|
|
|
|
|||
σ |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
||||
Таким образом, в нашем примере при |
zi = |
xi − xв |
, |
zi+1 |
= |
xi+1 − xв |
||
|
|
|||||||
|
|
σ |
в |
|
|
σ |
в |
|
|
|
|
|
|
|
|||
составляем расчетную таблицу (табл. 6.3)
92

|
|
|
|
|
|
|
Таблица 6.3 |
|
|
|
|
|
|
|
|
|
|
хi |
хi+1 |
zi |
zi+1 |
Ф(zi) |
Ф(zi+1) |
pi= Ф(zi+1)- Ф(zi) |
|
ni′=npi |
38 |
44 |
-∞ |
1,83 |
-0,5 |
-0,466 |
0,0336 |
|
3,36 |
44 |
50 |
1,83 |
1,16 |
-0,466 |
-0,377 |
0,0894 |
|
8,94 |
50 |
56 |
1,16 |
0,49 |
-0,377 |
-0,188 |
0,1891 |
|
18,91 |
56 |
62 |
0,49 |
0,17 |
-0,189 |
0,0675 |
0,2554 |
|
25,54 |
62 |
68 |
0,17 |
0,84 |
0,0675 |
0,2995 |
0,2320 |
|
23,20 |
68 |
74 |
0,84 |
1,51 |
0,2995 |
0,4345 |
0,1350 |
|
13,50 |
74 |
80 |
1,51 |
2,18 |
0,4345 |
0,4854 |
0,0509 |
|
5,09 |
80 |
86 |
2,18 |
+∞ |
0,4854 |
0,5 |
0,0146 |
|
1,46 |
|
|
|
|
|
|
∑ pi = 1 |
|
∑ni =100 |
Получаем таблицу для эмпирических и теоретических частот
(табл. 6.4).
|
|
|
|
|
|
|
Таблица 6.4 |
|
|
|
|
|
|
21 |
|
|
|
ni |
2 |
12 |
17 |
27 |
14 |
6 |
1 |
|
ni′ |
3,36 |
8,94 |
18,91 |
25,54 |
23,20 |
13,50 |
5,09 |
1,46 |
Проверяем гипотезу о нормальном распределении выборки Х с помощью критерия Пирсона. Объединяем малочисленные эмпирические ( ni < 5 ) и соответствующие им теоретические частоты
(табл. 6.5).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
|
|
14 |
|
|
|
|
17 |
|
27 |
|
|
|
21 |
|
14 |
|
7 |
||||||
ni′ |
|
|
12,30 |
|
|
|
18,91 |
|
25,54 |
|
23,20 |
|
13,50 |
|
6,55 |
|||||||||
Вычисляем наблюдаемое значение критерия Пирсона. |
|
|
||||||||||||||||||||||
χнабл2 |
= ∑ |
(ni − ni′)2 |
= |
(14 −12,30)2 |
+ |
(17 −18,91)2 |
+ |
(27 − 25,54)2 |
||||||||||||||||
|
|
|
|
18,91 |
25,54 |
|
|
|||||||||||||||||
|
|
|
|
|
ni′ |
|
12,30 |
|
|
|
|
|
||||||||||||
+ |
(21 |
− 23,20) |
2 |
+ |
(14 −13,50)2 |
|
+ |
(7 |
−6,55) |
2 |
= 0,71. |
|
|
|
|
|||||||||
|
|
23,30 |
|
|
13,50 |
|
|
|
6,55 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
По таблице критических точек распределения χ2 по заданному уровню значимости α = 0,05 и числу степеней свободы r =k-3
93

(k – число интервалов, оставшихся после объединения малочисленных частот) находим критическую точку правосторонней критической области (Приложение 3)
χкр2 (0,05;3) = 7,8.
Так как χнабл2 < χкр2 , то гипотезу о нормальном распределении исследуемой случайной величины принимаем.
6. Теоретическая плотность нормального распределения оп-
|
|
|
1 |
|
−( x−αx )2 |
|
ределяется формулой |
f (x) = |
|
|
e 2σx2 |
, где αx = xB , σч =σB |
|
σx |
|
2π |
||||
|
|
|
|
|
Таким образом, теоретическая плотность случайной величины
|
|
1 |
|
− |
( x−60,44)2 |
||
|
|
|
|
|
|
||
Х запишется в виде |
f (x) = |
|
|
e |
161,3 . |
||
8,98 |
2π |
||||||
|
|
|
|
|
|||
Для построения графика плотности распределения составляем расчетную таблицу (табл. 6.6).
Таблица 6.6
x |
ax − 3σx |
ax − 2σx |
ax −σx |
ax |
ax +σx |
ax + 2σx |
ax + 3σx |
f ( x ) |
0,0005 |
0,006 |
0,0269 |
0,0444 |
0,0269 |
0,006 |
0,0005 |
График теоретической плотности строим на одном рисунке с гистограммой (рис.6.2).
7. Для оценки неизвестного математического ожидания при неизвестном среднем квадратическом отклонении генеральной совокупности служит интервал
|
xB −ty |
δB |
< ax < xB +ty |
δB |
|
, |
|
|
|
n |
|||||
|
|
n |
|
|
|||
где ty = t(γ;n) |
– критическая точка |
распределения Стьюдента |
|||||
(Приложение |
4). По |
условию |
γ = 0,95 |
; n=100. Отсюда |
|||
tγ = t(0,95;100) =1,984.
94

Находим искомый интервал
60,44 −1,984 8,98100 < ax < 60,44 +1,984 8,98100 ,
или окончательно 58,66 < ax < 62,22 .
Производим расчет выборки Y.
1. По значениям выборки составляем вариационный ряд
(табл. 6.7).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
79 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
mi |
1 |
4 |
2 |
4 |
6 |
7 |
6 |
10 |
9 |
13 |
7 |
9 |
6 |
6 |
5 |
1 |
2 |
2 |
Определяем минимальное и максимальное значения выборки Y: ymin = 79 , ymax =97. Находим длину интервала
hy = |
|
|
ymax − ymin |
= |
|
97 −79 |
= 2,3486. |
|
1 |
+3,332 lg n |
1+3,332 lg100 |
||||||
|
|
|
||||||
Принимаем hy = 2 . Начало первого интервала yнач = ymin − hy / 2 = 78.
Составляем интервальный ряд распределения. Варианту, значение которой совпадает с нижней границей интервала, включаем в i-й интервал, а варианту, значение которой совпадает с верхней границей интервала, включаем в следующий (i + 1)-й интервал. Данные заносим в расчетную таблицу (табл. 6.8).
Таблица 6.8
Начало |
Конец |
Середи- |
Частота |
Относи- |
Плот- |
Накоп- |
на ин- |
тельная |
ность |
||||
интер- |
интерв. |
тервала |
интерв. |
частота |
частоты |
лен. |
вала yi |
yi+1 |
~ |
ni |
wi = ni / n |
wi / hx |
частоты |
|
|
yi |
|
|
||
78 |
80 |
79 |
1 |
0,01 |
0,005 |
0,01 |
80 |
82 |
81 |
4 |
0,04 |
0,020 |
0,05 |
82 |
84 |
83 |
6 |
0,06 |
0,030 |
0,11 |
82 |
86 |
85 |
13 |
0,13 |
0,065 |
0,24 |
95

Начало |
Конец |
Середи- |
Частота |
Относи- |
Плот- |
Накоп- |
на ин- |
тельная |
ность |
||||
интер- |
интерв. |
тервала |
интерв. |
частота |
частоты |
лен. |
вала yi |
yi+1 |
~ |
ni |
wi = ni / n |
wi / hx |
частоты |
|
|
yi |
|
|
||
86 |
88 |
87 |
16 |
0,16 |
0,080 |
0,40 |
88 |
90 |
89 |
22 |
0,22 |
0,110 |
0,62 |
90 |
92 |
91 |
16 |
0,16 |
0,080 |
0,78 |
92 |
94 |
93 |
12 |
0,12 |
0,060 |
0,90 |
94 |
96 |
95 |
6 |
0,06 |
0,030 |
0,96 |
96 |
98 |
97 |
4 |
0,04 |
0,020 |
1,00 |
2. Находим выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение для выборки Y.
|
|
~ |
|
|
|
|
|
+... +95 6 +97 |
|
|
|
|
|||
yB |
= |
∑yi ni |
|
= 79 1+81 4 |
4 =88,86. |
|
|
|
|||||||
n |
|
100 |
|
|
|
|
|
|
|||||||
D |
|
~ |
− yВ ) |
2 |
ni = (79 |
−88,86) |
2 |
1 |
+... |
+(97 −88,86) |
2 |
4 = |
|||
= ∑( yi |
|
|
|
||||||||||||
В |
|
|
|
n |
|
|
|
|
|
|
100 |
|
|
|
|
=15,7004. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
σВ = |
DВ = |
15,7004 = 3,96. |
|
|
|
|
|
|
|
||||||
3. Записываем эмпирическую функцию распределения (по значениям столбца табл. 6.8).
|
0 |
y ≤ 79 |
|
|
||
|
|
79 < y ≤81 |
||||
|
0,01 |
|||||
|
|
81 < y ≤83 |
||||
|
0,05 |
|||||
|
|
83 < y ≤85 |
||||
|
0,11 |
|||||
|
0,24 |
85 < y ≤87 |
||||
F * ( y) = |
0,40 |
87 |
< |
y |
≤ |
89 |
|
|
|
|
|||
|
0,62 |
89 < y ≤ 91 |
||||
|
|
91 < y ≤ 93 |
||||
|
0,78 |
|||||
|
|
93 < y ≤ 95 |
||||
|
0,90 |
|||||
|
|
95 < y ≤ 97 |
||||
|
0,96 |
|||||
|
1 |
y > 97 |
|
|
||
96
Строим график эмпирической функции распределения
(рис.6.3).
Рисунок 6.3
4.По интервальному ряду распределения (значения столбца
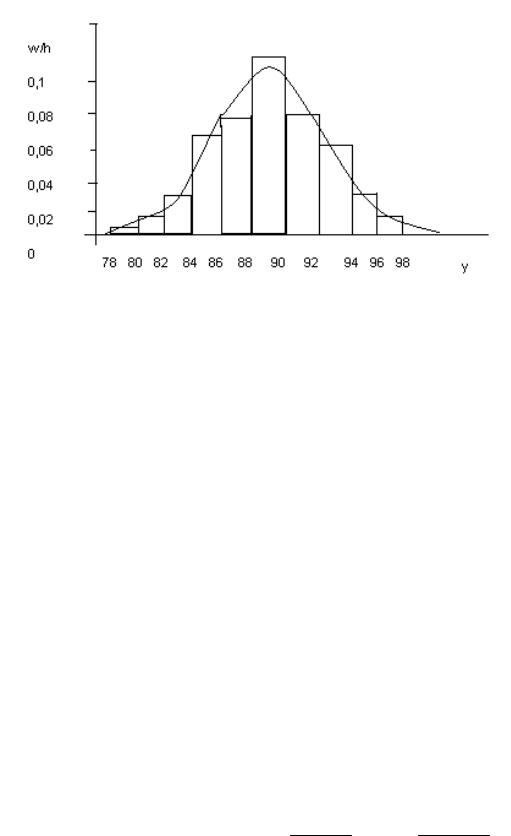
″wy / hy ″ табл. 6.8) строим гистограмму относительных частот
(рис. 6.4).
Рисунок 6.4
5. Проверяем гипотезу о нормальном законе распределения
y − y
случайной величины Y, положим zi = i σB B , zi+1 = .
Составляем расчетную таблицу (табл. 6.9).
97
Таблица 6.9
y |
y |
z |
|
z |
Ф(z |
) |
Ф(z |
|
) |
pi = Ф(zi+1) − |
n/ |
= np |
|
i |
i +1 |
|
i |
i+1 |
i |
|
|
i+1 |
|
−Ф(zi ) |
i |
|
i |
78 |
80 |
-∞ |
-2,24 |
-0,5 |
-0,4875 |
0,0125 |
1,25 |
|
|||||
80 |
82 |
-2,24 |
-1,73 |
-0,4875 |
-0,4582 |
0,0293 |
2,93 |
|
|||||
82 |
84 |
-1,73 |
-1,23 |
-0,4582 |
-0,3907 |
0,0675 |
6,75 |
|
|||||
84 |
86 |
-1,23 |
-0,72 |
-0,3907 |
-0,2642 |
0,1265 |
12,65 |
|
|||||
86 |
88 |
-0,72 |
-0,22 |
-0,2642 |
-0,0871 |
0,1771 |
17,71 |
|
|||||
88 |
90 |
-0,22 |
0,29 |
-0,0871 |
0,1141 |
0,2012 |
20,12 |
|
|||||
90 |
92 |
0,29 |
0,79 |
0,1141 |
0,2852 |
0,1711 |
17,11 |
|
|||||
92 |
94 |
0,79 |
1,30 |
0,2852 |
0,4032 |
0,1180 |
11,80 |
|
|||||
94 |
96 |
1,30 |
1,80 |
0,4032 |
0,4641 |
0,0609 |
6,09 |
|
|||||
96 |
98 |
1,80 |
+∞ |
0,4641 |
0,5 |
|
0,0359 |
3,59 |
|
||||
|
|
|
|
|
|
|
|
|
|
∑pi =1 |
∑ni/ =100 |
||
Получаем таблицу для эмпирических и теоретических частот
(табл. 6.10).
Таблица 6.10
ni |
1 |
4 |
6 |
13 |
16 |
22 |
16 |
12 |
6 |
4 |
ni/ |
1,25 |
2,93 |
6,75 |
12,65 |
17,71 |
20,12 |
17,11 |
11,80 |
6,09 |
3,59 |
Проверяем гипотезу о нормальном распределении выборки Y с помощью критерия Пирсона.
Объединяем малочисленные эмпирические (ni<5) и соответствующие им теоретические частоты (табл. 6.11).
Таблица 6.11
|
ni |
5 |
|
|
|
|
|
6 |
|
|
|
13 |
|
|
|
16 |
|
22 |
|
16 |
|
|
|
|
12 |
|
10 |
|
|||||||
ni/ |
4,18 |
|
|
|
|
6,75 |
|
|
|
12,65 |
17,71 |
20,12 |
17,11 |
|
|
11,80 |
9,68 |
|
|||||||||||||||||
|
|
|
Вычисляем наблюдаемое значение критерия Пирсона |
|
|
||||||||||||||||||||||||||||||
χ2 |
|
(n |
i |
− n/ )2 |
|
(5 |
− 4,18)2 |
|
|
(6 |
− 6,75) |
2 |
(13 −12,65)2 |
|
(16 |
−17,71)2 |
|||||||||||||||||||
= ∑ |
|
|
|
|
i |
= |
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|||||||
|
|
n/ |
|
|
|
4,18 |
|
|
|
6,75 |
12,65 |
|
|
|
|
|
17,71 |
|
|||||||||||||||||
|
набл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
(22 − 20,12)2 |
+ |
(16 |
−17,11) |
2 |
+ |
|
(12 −11,80)2 |
|
+ |
(10 −9,68) |
2 |
= 0,81. |
|
|
|
||||||||||||||||||
|
|
20,12 |
|
|
|
|
|
|
17,11 |
|
|
|
11,80 |
|
|
9,68 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
98

По таблице критических точек распределения χ2 по заданному уровню значимости a =0,05 и числу степеней свободы r= k – 3 (k – число интервалов, полученных после объединения малочисленных частот) находим критическую точку правосторонней критической области (приложение 3)
χ2кр(0,05; 5)=11,1
Так как χ2набл<χ2кр, то гипотезу о нормальном распределении исследуемой случайно величины принимаем.
6. Записываем теоретическую плотность нормального распределения
|
|
|
|
|
1 |
|
|
|
( y −a y )2 |
|
1 |
|
|
|
( y −88,86)2 |
|
|
|
|
|
|
|
|
|
|
|
|
2σ y2 |
|
|
|
|
|
|
|
|
|||
|
|
f ( y) = |
|
|
|
e |
= |
|
|
e |
31,36 |
|
|
|
|
||||
|
|
σ |
2π |
|
3,96 |
2π |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для построения графика плотности составляем расчетную |
|||||||||||||||||||
таблицу (табл. 6.12). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
ay –3σ |
|
ay –2σ |
|
|
ay –σ |
|
ay |
|
|
ay +σ |
|
|
ay +2σ |
ay +3σ |
||||
ƒ(y) |
0,0011 |
|
0,0136 |
|
0,0611 |
0,1007 |
|
0,0611 |
|
0,0136 |
0,0011 |
||||||||
График теоретической плотности строим на одном рисунке с гистограммой (рис. 6.4).
7. Находим доверительный интервал для оценки неизвестного математического ожидания
yв −tγ σnв < ay < yв +tγ σnв
По условию y=0,95; n=100. Находим ty = t(0,95; 100) = 1, 984 (Приложение 4).
Получаем искомый интервал
88,86 −1,984 3,96100 < ay <88,86 +1,984 3,96100
или окончательно 88,07 < ay < 89,65 .
По значениям интервалов, найденных для выборок X и Y, составляем корреляционную таблицу (табл. 6.13).
99
