3.Средняя арифметическая : простая и взвешенная, особенности их применения (указать формулы и дать примеры).
4.Свойства средней арифметической величины.
Понятие средней арифметической
Средняя арифметическая - такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий фонд заработной платы — это сумма заработных плат всех работников.
Средняя арифметическая может быть вычислена по формуле:
где n — численность совокупности.
Смотрите видео по нахождению средней арифметической величины
Виды средней арифметической величины
Средняя арифметическая величина используется в форме простой средней и взвешенной средней. Средняя арифметическая простая равна простой сумме отдельно взятых значений осредняемого признака, разделенная на общее число этих значений. В различных контрольных по статистике она используется тогда, когда имеются несгруппированные индивидуальные значения признака, и может быть вычислена по формуле:
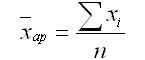
где n — общая численность совокупности значений х.
Средняя арифметическая взвешенная — это средняя из вариантов, которые повторяются разное число раз или имеют различный вес. Она может быть рассчитана по формуле:
Основные свойства средней арифметической
1. Если индивидуальные значения признака (варианты), уменьшить (увеличить) в n раз, то среднее значение нового признака соответственно уменьшится или увеличится во столько же.
2. Если все варианты осредняемого признака уменьшить (увеличить) на число А, то средняя арифметическая соответственно изменится на это же число.
3. Если вес всех осредняемых вариантов уменьшить (увеличить) в k раз, то средняя арифметическая не изменится.
4. Сумма отклонений отдельных значений признака от средней арифметической равна нулю.
Часто приходится вычислять среднюю по групповым средним или по средним отдельных частей совокупности. Например, средняя рождаемость в стране представляет собой среднее из средних рождаемости по отдельным регионам страны. Средние из средних определяются так же, как и средние из первоначальных значений признака.
5.Средняя гармоническая: простая и взвешенная, особенности их применения (указать формулы и дать примеры).
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.
Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
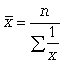(5.6)
К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость:
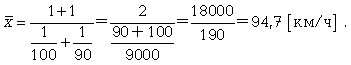
В
статистической практике чаще
используется 
гармоническая
взвешенная, формула которой имеет вид
(5.7)
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель.
Например, при расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров. Допустим, необходимо узнать среднюю цену реализованных товаров:
|
Вид товара |
Цена за единицу, руб. |
Сумма реализаций, руб. |
|
а |
50 |
500 |
|
б |
40 |
600 |
|
с |
60 |
1200 |
Получаем
6. Мода и медиана – структурные средние. (указать формулы и дать примеры).
Мода и медиана
Медиана в статистке
Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.
Посмотреть решение задачи на нахождение моды и медианы Вы можете здесь
В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:
где Хm — нижняя граница медианного интервала; im — медианный интервал; Sme— сумма наблюдений, которая была накоплена до начала медианного интервала; fme — число наблюдений в медианном интервале.
Свойства медианы
Медиана не зависит от тех значений признака, которые расположены по обе стороны от нее.
Аналитические операции с медианой весьма ограничены, поэтому при объединении двух распределений с известными медианами невозможно заранее предсказать величину медианы нового распределения.
Медиана обладает свойством минимальности. Его суть заключается в том, что сумма абсолютных отклонений значений х, от медианы представляет собой минимальную величину по сравнению с отклонением X от любой другой величины
Графическое определение медианы
Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив поп олам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы.
Определение моды в статистике
Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения. Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда.
Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле:
где ХМо — нижняя граница модального интервала; imo — модальный интервал; fм0, fм0-1,, fм0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах. Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д.