
- •Глава 3. Теория пределов
- •§ 3.1. Предел последовательности. Предел функции
- •§ 3.2. Бесконечно малые величины
- •§ 3.3. Арифметические свойства предела
- •§ 3.4. Предельный переход в неравенствах
- •§ 3.5. Односторонние пределы. Пределы при стремлении к бесконечности
- •§ 3.6.Первый замечательный предел
- •§ 3.7. Предел монотонной ограниченной функции
- •§ 3.8. Число e Теорема 3.8.1. Существует предел последовательности .
- •§ 3.9. Критерий Коши существования предела последовательности, предела функции
§ 3.8. Число e Теорема 3.8.1. Существует предел последовательности .
Доказательство. Сначала докажем лемму
Лемма 3.8.1. (неравенство Бернулли):
Если
 ,
то
,
то
Доказательство.
Используем
метод математической индукции. При имеем:
имеем: .
Предположим, что при
.
Предположим, что при неравенство
верно:
неравенство
верно: .
Тогда при
.
Тогда при +1
имеем:
+1
имеем:
 )=1+
)=1+ .
.
Неравенство доказано.
Чтобы
доказать существование предела
 ,
рассмотрим последовательность
,
рассмотрим последовательность
 .
Для членов этой последовательности :
.
Для членов этой последовательности :

Применим
неравенство Бернулли, выбрав

 :
:
 .
.
Таким
образом, . Так как
. Так как ,
то
,
то ,
поэтому рассматриваемая последовательность
убывает и ограничена снизу. Значит,
существует предел
,
поэтому рассматриваемая последовательность
убывает и ограничена снизу. Значит,
существует предел .
Так как
.
Так как , то и
, то и .
Следовательно,существует
предел
.
Следовательно,существует
предел

 .
.
Замечание.
Число,
равное пределу
 ,
обозначается
,
обозначается
 в честь великого математика Л. Эйлера(L.
Euler),
т.е.
в честь великого математика Л. Эйлера(L.
Euler),
т.е.

Замечание. Доказанное равенство носит название второго замечательного предела. Сего помощью будут вычислены производные показательной, логарифмической и степенной функции.
Теорема
3.8.2. Имеет
место равенство
Доказательство.
Докажем
сначала, что
Обозначим
 целую часть отношения
целую часть отношения ,
, . Тогда справедливы неравенства:
. Тогда справедливы неравенства: .
Перепишем их в виде
.
Перепишем их в виде .
Тогда
.
Тогда При этом
При этом ,
,

В полученных неравенствах левая и правая части стремятся к e, т.к.

Таким
образом, по теореме 3.4.3 получаем, что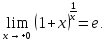
Для
строгого доказательства того, что
 ,
потребуется теорема 4.1.3, доказанная в
следующей главе .
,
потребуется теорема 4.1.3, доказанная в
следующей главе .
Обозначим
 .
Получаем, что
.
Получаем, что
 .
Выражение
.
Выражение
 при
при стремится
к 0, но не принимает значение 0 в левой
проколотой окрестности точки
стремится
к 0, но не принимает значение 0 в левой
проколотой окрестности точки .
Обозначив
.
Обозначив получаем,
что
получаем,
что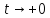 ,
когда
,
когда Тогда
используя теорему 4.1.3 и равенство
Тогда
используя теорему 4.1.3 и равенство
 ,
,
получаем,
что выражение
 стремится
кe
при
стремится
кe
при
 ,
т.к.
,
т.к. . Теорема доказана.
. Теорема доказана.
§ 3.9. Критерий Коши существования предела последовательности, предела функции
Определение
3.9.1.
Пусть задана последовательность
 и пусть
и пусть
 - возрастающая последовательность
натуральных чисел. Тогда последовательность
- возрастающая последовательность
натуральных чисел. Тогда последовательность подпоследовательность
исходной
последовательности.
подпоследовательность
исходной
последовательности.
Теорема
3.9.1.
Последовательность
 имеет пределA
тогда и только тогда, когда любая её
подпоследовательность имеет предел,
равный A.
имеет пределA
тогда и только тогда, когда любая её
подпоследовательность имеет предел,
равный A.
Доказательство.
Поскольку последовательность сама
является одной из своих подпоследовательностей
( для которой
 ),
утверждение теоремы очевидно в одну
сторону. Обратно, из определения
подпоследовательности сразу вытекает,
что для любого
),
утверждение теоремы очевидно в одну
сторону. Обратно, из определения
подпоследовательности сразу вытекает,
что для любого
 выполняется неравенство
выполняется неравенство .
Если
.
Если ,то
для любого
,то
для любого существует
существует такое, что при
такое, что при выполняется неравенство
выполняется неравенство .При
этом для любой подпоследовательности
.При
этом для любой подпоследовательности при
при выполняется
неравенство
выполняется
неравенство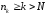 ,
из которого следует, что
,
из которого следует, что .
Это означает, что
.
Это означает, что .
.
Определение 3.9.2. Частичным пределом последовательности называется предел некоторой её подпоследовательности.
Замечание. Теорема означает, что последовательность имеет предел тогда и только тогда, когда любая её подпоследовательность имеет частичный предел и все эти пределы одинаковы.
Теорема 3.9.2. (Лемма Больцано-Вейерштрасса) Из любой ограниченной бесконечной последовательности можно извлечь подпоследовательность, сходящуюся к конечному пределу.
Доказательство.
Если
множество значений , которые принимает
последовательность
 конечное,
т.е.
конечное,
т.е. ,
то хотя бы одно из значений
,
то хотя бы одно из значений , обозначим его
, обозначим его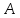 ,
она принимает бесконечно много раз,
т.е. существует бесконечное множество
номеров
,
она принимает бесконечно много раз,
т.е. существует бесконечное множество
номеров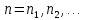 таких,
что
таких,
что .
Поэтому
.
Поэтому
 ,
подпоследовательность
,
подпоследовательность .
искомая.
.
искомая.
Рассмотрим
теперь случай, когда множество значений
бесконечное. Так как это множество, по
условию, ограниченное, по теореме 2.7.1
существует предельная точка этого
множества, обозначим её A.
Покажем, что существует последовательность
 такая, что
такая, что .
По определению предельной точки, для
.
По определению предельной точки, для существует номер
существует номер такой, что
такой, что .
Положим
.
Положим .
Существует
.
Существует такое, что
такое, что .
Точки различны,
.
Точки различны,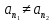 ,
т.к.
,
т.к. , а номер
, а номер выбираем так, чтобы выполнялось
неравенство
выбираем так, чтобы выполнялось
неравенство ,
что можно сделать, так как, по теореме
2.7.2, в любой окрестности предельной
точки содержится бесконечное число
элементов этого множества. Далее,
,
что можно сделать, так как, по теореме
2.7.2, в любой окрестности предельной
точки содержится бесконечное число
элементов этого множества. Далее, .
Как и раньше, выбираем
.
Как и раньше, выбираем так,
что
так,
что
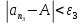 и
и . Продолжая этот процесс, получаем
последовательность
. Продолжая этот процесс, получаем
последовательность такую, что
такую, что ,
что означает, что
,
что означает, что .
.
Замечание. Отметим, что невзирая на определённое сходство между собой, понятия частичного предела последовательности и предельной точки множества её значений не совпадают. В первом случае доказанной теоремы у множества значений последовательности нет предельных точек, т.к. оно конечное (см. следствие теоремы 2.7.2.) Второй случай доказанной теоремы означает, что предельная точка множества значений последовательности является её частичным пределом.
Определение
3.9.3. Последовательность
 называетсяфундаментальной,
если для любого
называетсяфундаментальной,
если для любого
 существует
такое число
существует
такое число ,
что для всех
,
что для всех ,
выполнено неравенство
,
выполнено неравенство .
.
Теорема 3.9.3. (Критерий Коши для последовательности) Предел последовательности существует тогда и только тогда, когда эта последовательность является фундаментальной.
Доказательство.
Докажем сначала необходимость, т.е. что
если последовательность имеет предел,
то она фундаментальная. Из определения
предела следует, что для
любого
 существует
такое число
существует
такое число ,
что для всех
,
что для всех ,имеем:
,имеем: ,
, .
. Используем
известное неравенство для модулей:
Используем
известное неравенство для модулей:
 .
Обозначив
.
Обозначив ,
получаем:
,
получаем: +
+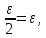 т.е. из существования предела
последовательности следует ее
фундаментальность.
т.е. из существования предела
последовательности следует ее
фундаментальность.
Доказательство
достаточности проведём в три этапа.
Во-первых,докажем, что из фундаментальности
последовательности следует ее
ограниченность. Действительно, пусть
 .
Тогда существует
.
Тогда существует такое, что для всех
такое, что для всех имеет место неравенство
имеет место неравенство .
Положим
.
Положим
 .
Тогда для всех
.
Тогда для всех
 ,
т.е.
,
т.е.
 .
Пусть
.
Пусть .
Из этих неравенств тогда следует, что
при
.
Из этих неравенств тогда следует, что
при имеем:
имеем:
 .
Положим
.
Положим
 .
Теперь для всех
.
Теперь для всех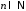 имеет место неравенство
имеет место неравенство
 ,
т.е. последовательность ограниченная
. Во-вторых, по теореме 3.9.2 существует
подпоследовательность
,
т.е. последовательность ограниченная
. Во-вторых, по теореме 3.9.2 существует
подпоследовательность
 такая, что она имеет некоторый предел
такая, что она имеет некоторый предел , т.е.
, т.е.
 .
В-третьих, докажем, что
вся последовательность имеет тот же
предел, т.е . что
.
В-третьих, докажем, что
вся последовательность имеет тот же
предел, т.е . что .
Доказано, что
.
Доказано, что и дано, что
и дано, что .
.
Если
 и если
и если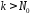 ,
то
,
то ,
поэтому
,
поэтому
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Теорема
3.9.4 .(Критерий
Коши для функции) Условие Коши :
для любого существует число
существует число , такое, что для любых
, такое, что для любых
 из
из
 разность
значений функции
разность
значений функции
 в этих точках по абсолютной величине
меньше
в этих точках по абсолютной величине
меньше ,
равносильно тому, что существует предел
этой функции при
,
равносильно тому, что существует предел
этой функции при .
.
Доказательство. Сначала докажем, что из существования предела следует условие Коши.
Пусть
существует предел
 .
Тогда,
.
Тогда,
 . Так как
. Так как
 ,
то
,
то
 . Следовательно,
. Следовательно,

Чтобы
доказать достаточность сначала дадим
ещё одно определение предела функции
при
 и докажем теорему о равносильности двух
определений предела.
и докажем теорему о равносильности двух
определений предела.
Определение
3.9.4.(
предела
функции
 при
при
 по Гейне
). Говорят, что функция
по Гейне
). Говорят, что функция
 имеет
при
имеет
при
 предел
предел ,
если для любой последовательности
,
если для любой последовательности
 такой, что
такой, что и такой, что для всех
и такой, что для всех выполнено неравенство
выполнено неравенство ,
существует предел
,
существует предел

Теорема 3.9.5. Определение 3.1.3, т.е. определение предела по Коши, равносильно определению 3.9.4 предела по Гейне.
Доказательство. Пусть сначала функция имеет предел по Коши.
Рассмотрим
произвольную последовательность
 такую, что
такую, что
 и такую, что для всех
и такую, что для всех выполнено неравенство
выполнено неравенство .
По определению предела по Коши,
.
По определению предела по Коши,
 .
.
По
определению предела последовательности,
 .Значит,
при
.Значит,
при
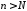 выполняется условие
выполняется условие ,
из которого сразу следует неравенство
,
из которого сразу следует неравенство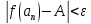 , означающее, что
, означающее, что ,
Тем самым, предел этой функции по Гейне
также существует.
,
Тем самым, предел этой функции по Гейне
также существует.
Предположим
теперь, что предел по Коши не существует
и докажем, что не существует и предел
по Гейне. По предположению, существует
такое число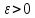 ,
что для любого числа
,
что для любого числа существует такая точка
существует такая точка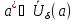 ,
что
,
что .
Последовательно выбирая в качестве
.
Последовательно выбирая в качестве числа
числа ,
находим точки
,
находим точки такие, что
такие, что .
Эти точки представляют собой
последовательность точек, удовлетворяющую
всем условиям, входящим в определение
предела по Гейне, однако для этой
последовательности условие
.
Эти точки представляют собой
последовательность точек, удовлетворяющую
всем условиям, входящим в определение
предела по Гейне, однако для этой
последовательности условие не
выполнено.
не
выполнено.
Вернёмся к доказательству теоремы 3.9.4 и докажем , что из условия Коши вытекает, что функция имеет предел по Гейне.
Действительно,
возьмём
любую последовательность
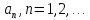 такую, что
такую, что и такую, что для всех
и такую, что для всех выполнено неравенство
выполнено неравенство .
Рассмотрим соответствующую
последовательность
.
Рассмотрим соответствующую
последовательность .
Зафиксируем
.
Зафиксируем и выберем соответствующее
и выберем соответствующее с помощью условия Коши. Так как
с помощью условия Коши. Так как ,
имеем:
,
имеем: .
Далее, при
.
Далее, при
 и ,по условию Коши ,
и ,по условию Коши , .
.
Значит,
 фундаментальная последовательность.
По теореме 3.9.3 существует предел
последовательности
фундаментальная последовательность.
По теореме 3.9.3 существует предел
последовательности , обозначим его
, обозначим его
Осталось
доказать, что если взять любую другую
последовательность
 такую, что
такую, что и такую, что для всех
и такую, что для всех выполнено неравенство
выполнено неравенство ,
то
,
то .
.
Для
этого рассмотрим последовательность
 . Это – последовательность точек,
сходящаяся к точке
. Это – последовательность точек,
сходящаяся к точке и
не принимающая значение
и
не принимающая значение ,
согласно своему определению. Поэтому
последовательность значений
,
согласно своему определению. Поэтому
последовательность значений также имеет предел, по доказанному выше.
Тогда по теореме 3.9.1 предел этой
последовательности равен пределу
подпоследовательности
также имеет предел, по доказанному выше.
Тогда по теореме 3.9.1 предел этой
последовательности равен пределу
подпоследовательности и пределу подпоследовательности
и пределу подпоследовательности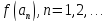 ,
равному
,
равному .
.
Теорема доказана.
