
- •Глава 3. Теория пределов
- •§ 3.1. Предел последовательности. Предел функции
- •§ 3.2. Бесконечно малые величины
- •§ 3.3. Арифметические свойства предела
- •§ 3.4. Предельный переход в неравенствах
- •§ 3.5. Односторонние пределы. Пределы при стремлении к бесконечности
- •§ 3.6.Первый замечательный предел
- •§ 3.7. Предел монотонной ограниченной функции
- •§ 3.8. Число e Теорема 3.8.1. Существует предел последовательности .
- •§ 3.9. Критерий Коши существования предела последовательности, предела функции
§ 3.6.Первый замечательный предел
Первый вопрос, который обычно возникает: чем же замечателен этот предел? Ответ прост – этот предел используется при вычислении производных тригонометрических функций.
Теорема 3.6.1. (первый замечательный предел)
 .
.
Замечание.
При доказательстве этой теоремы нельзя
применять правило Лопиталя, или формулу
Тейлора, т.к. хотя это и даст верный
результат, но будет являться логической
ошибкой, потому, что при вычислении
производной функции уже используется
то, что
 и в рассуждениях получается порочный
логический круг.
и в рассуждениях получается порочный
логический круг.
Доказательство.
|
|
Функция
|
Действительно,
в определении предела требуется, чтобы
для любого
 существовало хотя бы какое-нибудь число
существовало хотя бы какое-нибудь число для которого для всех
для которого для всех
 выполняется неравенство
выполняется неравенство Если же мы найдем число
Если же мы найдем число ,
для которого выполняется дополнительное
условие
,
для которого выполняется дополнительное
условие и для которого для всех
и для которого для всех выполняется неравенство
выполняется неравенство , то, тем самым, хотя бы какое-нибудь
, то, тем самым, хотя бы какое-нибудь будет найдено.
будет найдено.
Итак,
рассматриваем область
 .
Рассмотрим окружность единичного
радиуса и рассмотрим площади треугольников
.
Рассмотрим окружность единичного
радиуса и рассмотрим площади треугольников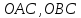 и
сектора
и
сектора .
Имеем:
.
Имеем:
 .
.
Далее, справедливы неравенства

означающие,
что при выполнены неравенства
выполнены неравенства

В свою очередь, эти неравенства равносильны неравенствам

Докажем,
что
 Для этого заметим, что
Для этого заметим, что Мы
только что доказали, что при
Мы
только что доказали, что при выполняется неравенство
выполняется неравенство Так как
Так как ,
по теореме 3.4.3
,
по теореме 3.4.3
 и,
значит,
и,
значит,
 .
Снова применяем теорему 3.4.3, из которой
следует, что
.
Снова применяем теорему 3.4.3, из которой
следует, что
 и, значит,
и, значит,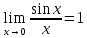 .
.
§ 3.7. Предел монотонной ограниченной функции
Определение
3.7.1. Последовательность
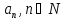 называетсянеубывающей
, если для всех
называетсянеубывающей
, если для всех
 выполняется
неравенство
выполняется
неравенство .
Она называетсявозрастающей,
если выполняется неравенство
.
Она называетсявозрастающей,
если выполняется неравенство .
Последовательность
.
Последовательность называетсяневозрастающей
,
называетсяневозрастающей
,
 выполняется
неравенство
выполняется
неравенство .
Она называетсяубывающей,
если выполняется неравенство
.
Она называетсяубывающей,
если выполняется неравенство .Общее
название всех таких последовательностей
–монотонные
последовательности.
.Общее
название всех таких последовательностей
–монотонные
последовательности.
Определение
3.7.2. Функция
 ,
определенная на промежутке
,
определенная на промежутке называется:неубывающей(возрастающей)
на
называется:неубывающей(возрастающей)
на , если для всех
, если для всех из
неравенства
из
неравенства следует неравенство
следует неравенство (
( ).
Она называетсяневозрастающей(убывающей)
на
).
Она называетсяневозрастающей(убывающей)
на , если из
, если из следует
следует (
( ).
Общее название для этих случаев –монотонные
на Х функции.
).
Общее название для этих случаев –монотонные
на Х функции.
Теорема 3.7.1 (К. Вейерштрасс)
Если последовательность
 не
убывает и ограничена сверху, то существует
не
убывает и ограничена сверху, то существует
 .
.Если последовательность
 не
возрастает и ограничена снизу, то
существует
не
возрастает и ограничена снизу, то
существует
 .
.
Доказательство.
Проведем
доказательство первого случая. Второй
случай совершенно аналогичен. По условию,
множество значений, которые принимает
последовательность
 ,
ограничено сверху. По теореме 2.5.1.
существует его точная верхняя грань A.
Докажем, что
,
ограничено сверху. По теореме 2.5.1.
существует его точная верхняя грань A.
Докажем, что
 .
Для этого возьмем произвольное
.
Для этого возьмем произвольное .
По определению
А,
любое меньшее число, в частности число
.
По определению
А,
любое меньшее число, в частности число
 ,
уже не является верхней гранью множества
значений, принимаемых последовательностью
,
уже не является верхней гранью множества
значений, принимаемых последовательностью .
Значит, при некотором
.
Значит, при некотором выполняется неравенство
выполняется неравенство или
или Кроме того,
Кроме того,
 ,
т.к.А
–
верхняя грань множества значений
,
т.к.А
–
верхняя грань множества значений
 .
Итак,
.
Итак, .
Но при
.
Но при
 выполнено неравенство
выполнено неравенство
 поэтому
поэтому . Таким образом, для любого
. Таким образом, для любого существует
существует
 такое,
что для всех
такое,
что для всех выполняется неравенство
выполняется неравенство . Поэтому
. Поэтому
 .
.
Теорема 3.7.2 (К. Вейерштрасс)
Если
 не
убывает на
не
убывает на и ограничена сверху на
и ограничена сверху на , то существует
, то существует .
.Если
 не
убывает на
не
убывает на и ограничена снизу на
и ограничена снизу на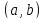 , то существует
, то существует .
.Если
 не
возрастает на
не
возрастает на и ограничена сверху на
и ограничена сверху на , то существует
, то существует .
.Если
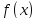 не
возрастает на
не
возрастает на и ограничена снизу на
и ограничена снизу на , то существует
, то существует .
.
Доказательство.
Оно
вполне аналогично теореме 3.7.1. Для
полноты изложения докажем, например,
случай 2. Поскольку множество значений,
принимаемых
 на интервале
на интервале
 ограничено снизу, существует
ограничено снизу, существует
 .
Докажем, что
.
Докажем, что
 .
Пусть
.
Пусть
 .
По определению точной нижней грани
множества, число
.
По определению точной нижней грани
множества, число уже не является нижней гранью множества
значений
уже не является нижней гранью множества
значений на
на
 ,
поэтому существует такое число
,
поэтому существует такое число ,
что
,
что .
Но тогда для всех
.
Но тогда для всех имеем
имеем , откуда
, откуда .
Значит, для всякого
.
Значит, для всякого найдено число
найдено число такое, что для всех
такое, что для всех выполняется неравенство
выполняется неравенство ,
т.е.
,
т.е.
 .
.
Следствие.
Если - монотонная на
- монотонная на функция, то для любого
функция, то для любого
 существуют
существуют
 и
и .
.
Доказательство.
Достаточно применить теорему 3.7.2 к
интервалам
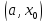 и
и .
.


 четная.
Поэтому если доказать, что
четная.
Поэтому если доказать, что ,
то и
,
то и ,
и по теореме 3.5.1. тогда
,
и по теореме 3.5.1. тогда . В определении предела при
. В определении предела при можно
дополнительно требовать выполнение
условия
можно
дополнительно требовать выполнение
условия .
.