
- •Глава 3. Теория пределов
- •§ 3.1. Предел последовательности. Предел функции
- •§ 3.2. Бесконечно малые величины
- •§ 3.3. Арифметические свойства предела
- •§ 3.4. Предельный переход в неравенствах
- •§ 3.5. Односторонние пределы. Пределы при стремлении к бесконечности
- •§ 3.6.Первый замечательный предел
- •§ 3.7. Предел монотонной ограниченной функции
- •§ 3.8. Число e Теорема 3.8.1. Существует предел последовательности .
- •§ 3.9. Критерий Коши существования предела последовательности, предела функции
Глава 3. Теория пределов
Понятие предельного перехода является основным в курсе математического анализа. С его помощью определяются производная функции и интеграл от функции. Предельный переход позволяет строить обобщения математических понятий, например, с его помощью строится несобственный интеграл. Предельный переход – непростое понятие и цель этой главы состоит в том, чтобы дать его подробное описание.
§ 3.1. Предел последовательности. Предел функции
Определение
3.1.1.
Если
каждому
 сопоставлено число
сопоставлено число ,
то говорят, что
задана
последовательность
,
то говорят, что
задана
последовательность
 Иными словами, последовательность
представляет собой отображение множества
натуральных чисел во множество
действительных чисел.
Иными словами, последовательность
представляет собой отображение множества
натуральных чисел во множество
действительных чисел.
Некоторые последовательности обладают очень важным свойством – они имеют предел. Дадим определение этого свойства.
Определение
3.1.2.
Последовательность
 имеет
предел,
равный числу
имеет
предел,
равный числу
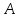 тогда и только тогда, когда для любого
тогда и только тогда, когда для любого
 существует число
существует число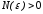 такое,
что для всех
такое,
что для всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству , выполняется неравенство
, выполняется неравенство .
.
Удобно
записывать это определение с помощью
логических символов:



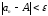 .
.
Для
обозначения предела последовательности
используется символ:
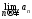 .
.
Примеры.
1) Если
 для
всех n,
то
для
всех n,
то
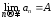
Доказательство.
Для любого
 и любого
и любого ,
и любого
n
,
и любого
n
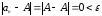 .
.
2)
Если
 ,
то
,
то
Доказательство.
Пусть
 .
Возьмем
.
Возьмем .
Тогда если
.
Тогда если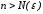 ,
то
,
то и
и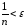 ,
поэтому
,
поэтому .
.
Замечание. Не следует отождествлять понятие предела последовательности и предельной точки множества значений, принимаемых последовательностью. В первом из приведённых выше примеров последовательность имеет предел, но множество её значений состоит из одной точки и не имеет предельных точек. Во втором примере предельная точка множества значений – точка 0 – совпадает с пределом последовательности. Может оказаться и так, что предельная точка множества значений не является пределом последовательности( а является так называемым частичным пределом последовательности). Определение частичного предела и соответствующий пример будут приведены ниже.
Перейдём
к определению понятия предела функции.
Пусть
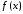 определена
в некоторой проколотой окрестности
определена
в некоторой проколотой окрестности точкиа.
(Отметьте, что функция
точкиа.
(Отметьте, что функция может быть не определена в самой точке
может быть не определена в самой точке
Определение
3.1.3.
Говорят,
что функция имеет
при
имеет
при
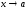 предел,
равный числу
А ,
когда для любой окрестности
предел,
равный числу
А ,
когда для любой окрестности точки
точки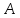 существует
проколотая окрестность
существует
проколотая окрестность точки
точки

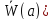 такая,
что выполняется включение
такая,
что выполняется включение ,
что равносильно тому, что для любого
,
что равносильно тому, что для любого .
выполняется
.
выполняется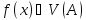 . С помощью логических символов это
определение записывается так:
. С помощью логических символов это
определение записывается так:

Данное определение называется определением предела функции по Коши.
Приведённое
определение носит общий характер. Точно
такое же определение имеют понятия
предела функции нескольких переменных,
предела отображения. Для того, чтобы
сделать это определение более удобным,
переформулируем его для функций одной
переменной, взяв вместо произвольной
окрестности
 рассматривать
рассматривать
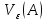 при произвольном
при произвольном и, соответственно, вместо
и, соответственно, вместо проколотую окрестность
проколотую окрестность .
Тогда оно примет вид:
.
Тогда оно примет вид:
 .
.
Вспоминая,
что условие
 равносильно неравенствам
равносильно неравенствам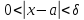 ,
а условие
,
а условие равносильно условию
равносильно условию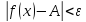 ,
получаем равносильную определению
3.1.3 запись определения предела, так
называемое определение предела на
"языке
,
получаем равносильную определению
3.1.3 запись определения предела, так
называемое определение предела на
"языке ":
":
 .
.
Следующая теорема означает, что понятие предела хорошо определено, т.е. если предел существует, то он определён однозначно.
Теорема
3.1.1. Если
предел последовательности существует, то он единствен, т.е. если
существует, то он единствен, т.е. если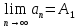 и если
и если , то
, то
Если
предел функции
 при
при существует,
то он единствен, т.е. если
существует,
то он единствен, т.е. если ,
, , то
, то .
.
Доказательство.
Предположим,
что последовательность имеет своим
пределом число ,
а также имеет пределом число
,
а также имеет пределом число ,
, .
Тогда выполняются утверждения:
.
Тогда выполняются утверждения:
 и
и
 При
При
 получаем, с одной стороны, что при
получаем, с одной стороны, что при
 выполняется неравенство
выполняется неравенство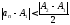 .
Аналогично, поскольку
.
Аналогично, поскольку
 - тоже предел, получаем, что при
- тоже предел, получаем, что при
 выполняется неравенство
выполняется неравенство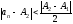 .
Пусть
.
Пусть
 .
Тогда при
.
Тогда при
 выполняются
условия
выполняются
условия и
и ,
поэтому выполняются и оба эти неравенства,
из которых следует, что
,
поэтому выполняются и оба эти неравенства,
из которых следует, что

Полученное противоречие доказывает первое утверждение теоремы.
Доказательство
второго утверждения этой теоремы
проводится вполне аналогично. Пусть
функция
 при
при
 два
различных предела,
два
различных предела, и
и
 .
Тогда, применяя определения предела
при
.
Тогда, применяя определения предела
при получаем,
что
для
получаем,
что
для
 существуют числа
существуют числа и
и такие, что при
такие, что при
 выполняется неравенство
выполняется неравенство
 ,
а при
,
а при выполняется неравенство
выполняется неравенство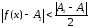 .
Тогда положим
.
Тогда положим
 и потребуем, чтобы выполнялись неравенства
и потребуем, чтобы выполнялись неравенства
 .
При этом
.
При этом

Полученное противоречие доказывает теорему.
