
shpora
.docx|
№1
Графики и свойства основных элементарных
функций.Показательные
функции:Определение.
Функция, заданная формулой у=ах (где
а>0, а≠1), называется показательной
функцией с основанием А.Основные
свойства показательной функции-Область
определения — множество (R) всех
действительных чисел.Область значений
— множество (R+) всех положительных
действительных чисел.При а > 1 функция
возрастает на всей числовой прямой;
при 0<а<1 функция убывает.Является
функцией общего вида. |
8.
Функции нескольких переменных и их
непрерывность. Определение-
пусть
имеется n
переменных величин,и каждому набору
их значение (х1,х2,…хn)
из некоторого множества Х соответствует
одно вполне определенное значение
множества переменной величины z.
Тогда говорят,что задана функция
нескольких переменных z=
f(x1,x2,…хn).
Переменные х1,…хn,
называются независимыми переменными,
или аргументами, z
– зависимой переменной, а символ f
означает закон соответствия. Множество
Х называется областью определения
функции. Очевидно, Х- подмножество
n-мерного
пространства. Функция
z=
a1x1+a2x2+…+anxn+b,
где а1,…аn,
b-
постоянные числа, называется линейной
. Её можно рассматривать как сумму n
линейных функций от переменных х1,..хn.
Функция
Непрерывность- Функция z= f(x,y) называется непрерывной в точке (х0,у0),если 1) она определена в точке (х0,у0), 2) имеет конечный предел при х→х0 и у→у0, 3) этот предел равен значению функции в точке (х0,у0). Т.е. lim f(x,y)= f(x0, y0) х→0 у→0 |
||
|
2. предел функции. Асимптоты графика функции.Число А называется пределом функции y=f(x) при x→∞, если для любого сколько угодно малого положительного числа Е, т.е. Е>0,Найдется такое положительное число S, зависящее от Е, что для всех таких х которые по модулю больше S, справедливо неравенство: |f(x) - A|<E; Число А называется пределом функции y=f(x) при x→х₀, если для любого сколько угодно малого положительного числа Е, т.е. Е>0,Найдется такое положительное число S, зависящее от Е, что для всех таких х≠х₀, которые удовлетворяют след неравенству (х- х₀)< S, справедливо неравенство: |f(x) - A|<E;
|
9.
Производные функции нескольких
переменных.
Частная производная функция нескольких
переменных по одной из этих переменных
называется предел отношения частного
приращения функции, приращению
рассматриваемой независимой переменно,
когда приращение стремится к нулю.
Определение. Частной
производной функции двух
переменных по одной из этих переменных
называется предел отношения
соответствующего частного приращения
функции к приращению рассматриваемой
независимой переменной при стремлении
последнего к нулю (если этот предел
существует).
Пусть
|
||
|
3.Основные
теоремы о пределах. Асимптоты графика
функции.
функция
не может иметь больше
одного предела,предел алгебраической
суммы равен сумме пределов,предел
произведения(частного 2х ф-ий) конечного
числа функций равен произведению
(частному этих ф-ий при усл. Что предел
делителя не равен 0)пределов этих
функций Предел
константы равен самой этой константе:
Прямая y = b называется горизонтальной
асимптотой графика
функции f (x) при x → +∞,
если
|
10
.Дифференциалы функции нескольких
переменных.
Дифференциалом дифференцируемой в
точке М(x₁,x₂,...,xп)
функции Z=f (x₁,x₂,...,xп)
называется главная линейная относительно
приращений аргументов часть приращения
этой функции в точке М . Если все
коэффициенты А в приращении функции
в точке независимой переменной можно
понимать любое число. Договоримся в
дальнейшем брать это число равным
приращению независимой переменной.
Дифференциалом функции называется
сумма произведений частных производных
этой функции на приращения соответствующих
независимых переменных- dz = z'x
|
||
|
4.Непрерывность функции в точке и на интервале. О1. Функция y=f(x) называется непрерывной в точке х₀ , если она определена в т х₀, т.е существует f(x₀) ,сущ предел ф-ии lim f(x) x→х₀,этот предел равен значению ф-ии в этой точке lim f(х₀) = f(x₀) x→х₀.О2. Функция называется непрерывной в точке , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.Функция называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.
|
11. Поиск экстремума функции одной переменной. 1.Найти производную функции.2. Приравнять эту производную к нулю и решить уравнение. Корни этого уравнения будут критическими точками.3. Определить характер каждого критического значения аргумента, для этого, выясним меняет ли знак производная при переходе аргумента через данное критическое значение. Если меняется то критическая точка является экстремума, если нет, то у этой точки нет мах и мин.
|
||
|
5.Точки разрыва первого и второго рода. Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке.Существуют левосторонний предел и правосторонний предел ;Эти односторонние пределы конечны.При этом возможно следующие два случая:Левосторонний предел и правосторонний предел равны друг другу: Такая точка называется точкой устранимого разрыва.Левосторонний предел и правосторонний предел не равны друг другу: Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов называется скачком функции. Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
|
12. Поиск экстремума функции двух переменных.1. Найти частные производные функции z’x и z’y , 2. Решить систему уравнений z’x=0, z’y = 0 и найти критические точки функции.,3. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличие экстремумов. 4. Найти экстремумы (экстремальные значения) функции. |
||
|
6. Производная и дифференциал.Пусть у=f(х) определена на промежутке Х, производной функции у=f(х) называется предел отношения приращения функции ∆у к приращению функции ∆х, когда ∆х⇨0.Дифференциалом функции называется, главное линейное отношение ∆х часть приращения функции, равное произведению производной на приращение независимой переменной.
|
13. Неопределенный интеграл, основные теоремы. Определение: совокупность всех первообразных у=f(х) на промежутке Х, называется неопределенным интегралом.Основные теоремы:производная от неопределенного интеграла равна подынтегральной функции,дифференциалом неопределенного интеграла является подынтегральное выражение,неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до последнего слагаемого,постоянный множитель можно выносить за знак интеграла,интеграл от алгебраической суммы равен сумме интегралов,интеграл от произведения равен произведению интегралов,интеграл от частного равен частному интегралов.
|
||
|
7. Основные теоремы о дифференцируемых функциях: : теорема Ферма, теорема Ролля, теорема Лагранжа.Теорема Ферма: если дифференцируемая на промежутке Х функция у=f(х) достигает своего наибольшего или наименьшего значения в точке х0 этого промежутка, то производная этой точки равна 0.Теорема Ролля: пусть функция у=f(х) удовлетворяет условиям:непрерывна на [a,b],является дифференцируемой на это отрезке,на концах отрезка принимает равные значения,тогда внутри отрезка существует хотя бы одна точка.Теорема Лагранжа: пусть функция у=f(х) удовлетворяет условиям:непрерывна на [a,b],является дифференцируемой на это отрезке,тогда внутри отрезка существует по крайней мере одна точка Е∈[a,b] в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке: f'(E)=(f(b)-f(a)/(b-a)).
|
14. Определенный интеграл, основные теоремы. Определение: определенным интегралом от непрерывной функции у=f(х) на отрезке (а,в) называют приращение какой-нибудь ее первообразной на этом отрезке. Теорема о среднем: если функция у=f(х) непрерывна на отрезке (а,в), где а больше в, то всегда найдется такое значение Е принадлежащие отрезку (а,в), что интеграл от а до в , будет представлен в виде b ∫f(x)dx=f(E)(b-a) a Теорема Ньютона-Лейбница: пусть функция у=f(х) непрерывна на отрезке (а,в) и F(х) – первообразная функции f(х) на отрезке (а,в), тогда определенный интеграл для функции у=f(х) на отрезке (а,в) равен приращению первообразной F(х) на отрезке (а,в)
∫f(x)dx=F(b)-F(a)
.
Если
|
||
|
15. Методы интегрирования: интегрирование подстановкой, интегрирование по частям, интегрирование рациональных функций.
Интегрирование
методом разложения.
Этот
метод основан на разложении
подынтегральной функции на сумму
функций, от каждой из которых
первообразную можно найти с помощью
таблицы или других методов.
Например
(х3
+ 3sinx
– 8) dx
=
х3
dx
+ 3sinx
dx
– 8dx
=<
используя формулы из таблицы>=
х4/4
3 cos
x
– 8 х
+ С.
Интегрирование
методом замены переменных.Интегрирование
этим методом заключается в приведении
данного интеграла к новому путем
замены переменной интегрирования х
на новую переменную z.
Пусть х
= g(z),
тогда dx
= g(
z)dz.
Поэтому
f(х)
dx
=
f
[g(z)]
g(
z)dz
= Ф (z)
+С = Ф [g-1(х)]
+ С.
Интегрирование
по частям.
Пусть
u(x)
и v(x)
– две функции от х,
имеющие непрерывные производные,
тогда справедлива следующая формула:
udv
= uv
-
vdu.
Интегрирование
рациональной дроби
. Задача
интегрирования сводится к интегрированию
простейших дробей следующих четырех
типов: Здесь, β=2, 3, …; λ=2, 3, …; B, M, N, b, p и q – некоторые вещественные числа, причем трехчлен x2+px+q не имеет вещественных корней, т.е. q-p2/4>0.
|
16. Прямая линия на плоскости. Условия перпендикулярности и параллельности двух прямых. Уравнение вида F(x,y)=0 есть уравнение линии на плоскости, если координаты всех точек, лежащих на этой линии удовлетворяют этому уравнению, а координаты точек, не лежащих на этой линии – не удовлетворяют Уравнение прямой, заданное уравнением первой степени общего вида Ax+By+C=0, называется уравнением прямой общего вида Рассмотрим случаи:
Исследуем уравнение (1).
ОПРЕДЕЛЕНИЕ Угловым коэффициентом прямой называется тангенс угла, на который нужно повернуть против часовой стрелки ось Ох вокруг начала координат О, чтобы прямая стала параллельна этой оси. Уравнение прямой, проходящей через заданную точку (уравнение пучка прямых) Любую прямую не параллельную оси Оу можно записать в виде у=кх+в.Пусть прямая проходит через точку М(х0,у0). тогда справедливо у0=кх0+в. Вычтем у-у0=к(х-х0).Уравнение прямой, проходящей через две заданные точки
Поделим
почленно
Условие параллельности прямых заключается в равенстве их угловых коэффициентов. tgφ1=tgφ2 или k1=k2.Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1,k1k2=-1
|
||
|
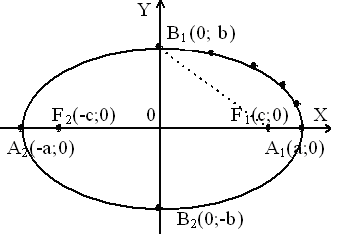
17. Эллипс: определение и вывод канонического уравнения.
Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина равная 2а.
F1(c,0),
F2(-c,0)
– фокусы эллипса.
A1(a,0),A2(-a,0),
B1(0,b),
B2(0,-b)
– вершины
эллипса
Пусть М (х;у) – произвольная точка эллипса. Т.к. MF1 + MF2 = 2a
Т.к.
|
1
18. Гипербола: определение и вывод канонического уравнения. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная. Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1 – MF2|=2a или MF1 – MF2 =±2a,
|
||
|
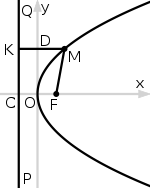
19. Парабола: определение и вывод канонического уравнения.
Каноническое уравнение параболы в прямоугольной системе координат:
|
20. Прямая и плоскость в пространстве. Точка пересечения прямой с плоскостью. Пусть плоскость Q задана уравнением общего типа: Ax+By+Cz+D=0, а прямая L в параметрическом виде: x=x1+mt, y=y1+nt, z=z1+pt, тогда чтобы найти точку пересечения прямой L и плоскости Q, нужно найти значение параметра t, при котором точка прямой будет лежать на плоскости. Подставив значение x, y, z, в уравнение плоскости и выразив t, получим
Значение t будет единственным, если прямая и плоскость не параллельны. Условия параллельности и перпендикулярности прямой и плоскости
Рассмотрим
прямую L:
б) параллельны друг
другу тогда и только тогда, когда
векторы Угол между прямой и плоскостью.
Пучок плоскостей Совокупность всех плоскостей, проходящих через заданную прямую L, называется пучком плоскостей, а прямая L - осью пучка. Пусть ось пучка задана уравнениями
Это уравнение имеет первую степень относительно х, у, z и, следовательно, при любом численном значении λ определяет плоскость. Так как данное уравнение есть следствие двух уравнений, то координаты точки, удовлетворяющие этим уравнениям будут удовлетворять и данному уравнению. Следовательно, при любом численном значении λ данное уравнение есть уравнение плоскости, проходящей через заданную прямую. Полученное уравнение есть уравнение пучка плоскостей. Уравнение вида F(x,y)=0 есть уравнение линии на плоскости, если координаты всех точек, лежащих на этой линии удовлетворяют этому уравнению, а координаты точек, не лежащих на этой линии – не удовлетворяют Уравнение прямой, заданное уравнением первой степени общего вида Ax+By+C=0, называется уравнением прямой общего вида Рассмотрим случаи:
Исследуем уравнение (1).
ОПРЕДЕЛЕНИЕ Угловым коэффициентом прямой называется тангенс угла, на который нужно повернуть против часовой стрелки ось Ох вокруг начала координат О, чтобы прямая стала параллельна этой оси. Уравнение прямой, проходящей через заданную точку (уравнение пучка прямых) Любую прямую не параллельную оси Оу можно записать в виде у=кх+в. Пусть прямая проходит через точку М(х0,у0). тогда справедливо у0=кх0+в. Вычтем у-у0=к(х-х0) Уравнение прямой, проходящей через две заданные точки
Поделим почленно
|
||
|
21.
Системы
линейных уравнений.
Обозначим
через
все возможности для произвольной системы ограничиваются следующими вариантами: 1. система совместна и имеет единственное решение; 2. cистема совместна и имеет бесконечное множество решений; 3. cистема несовместна.
При
этом все решения будут находиться в
том же множестве
|
22. Матрицы и их классификация. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.
*Матрицы равны между собой, если равны все их соответствующие элементы. *Матрица, у которой число строк и столбцов равно – называется квадратной. *Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной. *Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е. *Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной. *Матрица, у которой все элементы равны нулю, называется нулевой.
|
||
|
23. Операции над матрицами. Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицыодинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов. Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами:
Разность двух матриц:
Умножение матрицы на число - процесс, заключающийся в умножении числа на каждый элемент матрицы. Например, пусть дана матрица А:
Умножим число 3 на матрицу А:
Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы. Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца. Можно представить все это в виде схемы:
После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц, можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д.
|
24. Определители и их свойства. Теорема Лапласа. Понятие определителя n-го порядка Пусть дана квадратная таблица, состоящая из чисел, расположенных в n горизонтальных и в nвертикальных рядах. С помощью этих чисел по определённым правилам вычисляют некоторое число, которое называют определителем n-го порядка и обозначают следующим образом:
Воображаемая прямая, соединяющая элементы определителя, у которых оба индекса одинаковы, т.е. элементы
|
||
|
25
Обратная матрица: определение и
алгоритм вычисления.Обратная
матрица.
Для
каждого числа
|
26. N-мерное линейное векторное пространство. N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х1,х2,…хn) , где хi – i-я компонента вектора Х. Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. Х=У, если xi=yi, i=1…n. Суммой двух векторов одинаковой размерности n называется вектор Z=X+Y, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. zi=xi+yi , i=1…n. Произведением вектора Х на действительное число λ называется вектор V=λX, компоненты которого равны произведению λ на соответствующие компоненты вектора Х, т.е. vi=λxi , i=1…n.
|

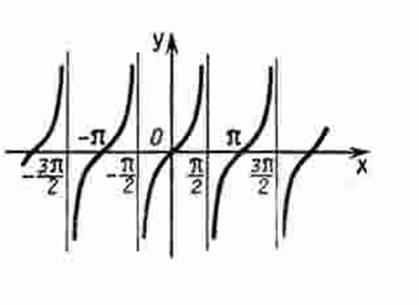 -Рис.
13 График функции
-Рис.
13 График функции 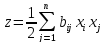 ( bij-
постоянные числа) называется
квадратической. В отличие от предыдущего
примера квадратичная функция не
является сепарабельной, т.е. не
раскладывается на сумму функций одной
переменной. Логарифмическая функция
( bij-
постоянные числа) называется
квадратической. В отличие от предыдущего
примера квадратичная функция не
является сепарабельной, т.е. не
раскладывается на сумму функций одной
переменной. Логарифмическая функция
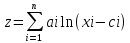 ,
где аi>0,
xi>ci>=0.
Функция постоянной эластичности
,
где аi>0,
xi>ci>=0.
Функция постоянной эластичности
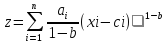 ,
где аi>0,
0<bi<1,
xi>ci>=0.
Производственная функция – z-величина
общественного продукта,х1-затраты
труда, х2- объем производственных
фондов),полагая для простоты n=2:
1) Функция Кобба-Дугласа – z
=b0x1b1x2b2,
2) функция с постоянной эластичностью
замещения: z=
e0
[e1x1-в+e2x2
-в].
,
где аi>0,
0<bi<1,
xi>ci>=0.
Производственная функция – z-величина
общественного продукта,х1-затраты
труда, х2- объем производственных
фондов),полагая для простоты n=2:
1) Функция Кобба-Дугласа – z
=b0x1b1x2b2,
2) функция с постоянной эластичностью
замещения: z=
e0
[e1x1-в+e2x2
-в]. x+
z’y
∇y.
Теорема: если частные производные
функции z’y
(x,y)
существует в окрестности точки (х, у)
и непрерывны в самой точке (х, у), то
функция z=
f(
x,
y)
дифференцируется в этой точке.
x+
z’y
∇y.
Теорема: если частные производные
функции z’y
(x,y)
существует в окрестности точки (х, у)
и непрерывны в самой точке (х, у), то
функция z=
f(
x,
y)
дифференцируется в этой точке.
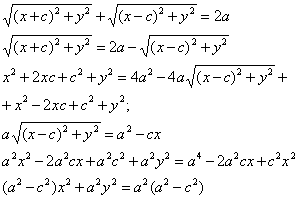
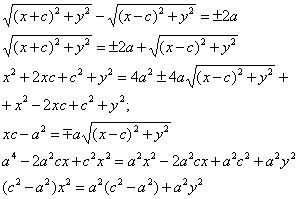

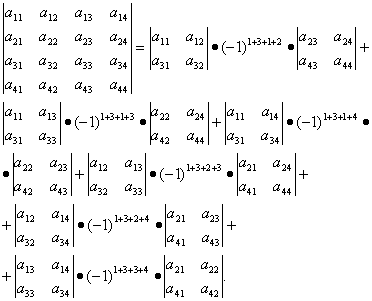 Теорема
Лапласа позволяет сводить вычисление
определителя n-го
порядка к вычислению нескольких
определителей порядка k < n .
Этих новых определителей оказывается
довольно много и поэтому теорему
Лапласа применять целесообразно лишь
в том случае, когда в определителе
можно так выбрать k строк,
что многие из миноров k-го
порядка, расположенных в этих строках,
будут равны нулю.
Теорема
Лапласа позволяет сводить вычисление
определителя n-го
порядка к вычислению нескольких
определителей порядка k < n .
Этих новых определителей оказывается
довольно много и поэтому теорему
Лапласа применять целесообразно лишь
в том случае, когда в определителе
можно так выбрать k строк,
что многие из миноров k-го
порядка, расположенных в этих строках,
будут равны нулю.