
- •Глава 10. Дифференциальное исчисление функций нескольких переменных
- •§10.1. Дифференцируемость функции многих переменных
- •10.1.1.Определение дифференцируемости функции многих переменных. Частные производные
- •10.1.2. Достаточное условие дифференцируемости функции нескольких переменных
- •§10.2. Дифференциал функции многих переменных и дифференциал отображения
- •10.2.1. Дифференциал функции многих переменных
- •10.2.2 Дифференциал отображения
- •§10.3. Производная сложной функции. Инвариантность формы первого дифференциала. Свойства матрицы Якоби
- •10.3.1. Производная сложной функции
- •10.3.2. Инвариантность формы первого дифференциала
- •10.3.3. Свойства матрицы Якоби. Якобиан
- •§10.4.Геометрические приложения
- •10.4.1. Касательная плоскость
- •10.4.2. Производная по направлению, градиент
- •§10.5.Производные и дифференциалы высших порядков
- •10.5.1. Производные высших порядков
- •10.5.2. Дифференциалы высших порядков
- •10.5.3.Второй дифференциал функции. Матрица Гессе
10.5.3.Второй дифференциал функции. Матрица Гессе
Вернемся
к формуле (25).
Она означает, что второй дифференциал
является квадратичной формой от
переменных
![]() .
Как известно из курса алгебры, квадратичной
форме сопоставляется матрица квадратичной
формы, в рассматриваемом случае имеющая
вид
.
Как известно из курса алгебры, квадратичной
форме сопоставляется матрица квадратичной
формы, в рассматриваемом случае имеющая
вид
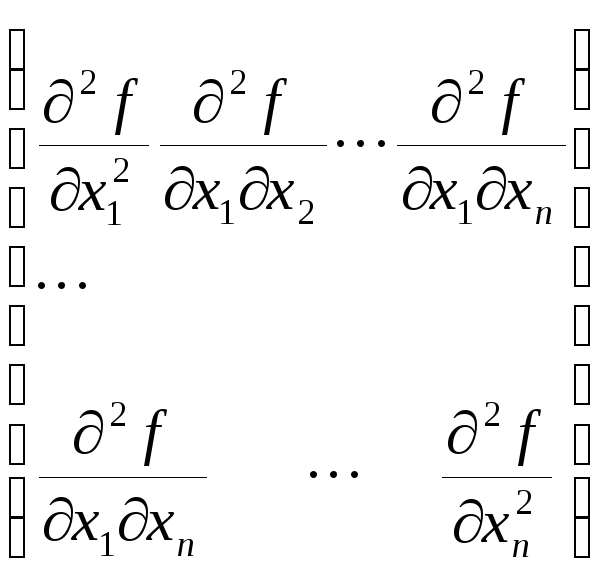 ,
где
все производные вычислены в рассматриваемой
точке и
называемая иногда матрицей
Гессе.
,
где
все производные вычислены в рассматриваемой
точке и
называемая иногда матрицей
Гессе.
§.10.6.Формулы Тейлора.
Теорема 10.7.Пусть
функция
![]() ,
,![]() имеет непрерывные производные до порядка
имеет непрерывные производные до порядка
![]() включительно в окрестности
включительно в окрестности
![]() точки
точки![]() и непрерывные производные порядка
и непрерывные производные порядка![]() в
в![]() .
Тогда для любой точки
.
Тогда для любой точки
![]()
![]() существует число
существует число![]() ,
,![]() такое, что
такое, что (29) ,
(29) ,
где все дифференциалы
вычислены при
![]() .
.
►Соединим в
пространстве ![]() точку
точку
![]() с точкой
с точкой![]() прямолинейным отрезком; запишем
параметрические уравнения этого отрезка:
любая его точка
прямолинейным отрезком; запишем
параметрические уравнения этого отрезка:
любая его точка![]() имеет вид
имеет вид
![]() (30) .
(30) .
При
![]() получаем
получаем![]() ,
при
,
при![]() получаем
получаем![]() .
.
Рассмотрим функцию
одной переменной
![]() ,
определенную на отрезке
,
определенную на отрезке![]() .
Уравнение (30) имеет вид уравнения (28).
.
Уравнение (30) имеет вид уравнения (28).
Поэтому, при
вычислении
![]() получаем, в соответствии с (26), что
получаем, в соответствии с (26), что![]() ,
,![]() ,
,![]() (31)
(31)
Осталось применить
к функции
![]() теорему 7.5:
теорему 7.5:
![]() (32)
(32)
Подставляя в (32) равенства (31), получаем утверждение теоремы.◄
Теорема 10.8. Пусть
функция
![]() имеет непрерывные производные до порядка
имеет непрерывные производные до порядка![]() включительно в
включительно в![]() точки
точки![]() .
Тогда
.
Тогда ,
где
,
где
![]() .
(33)
.
(33)
►Для доказательства
достаточно использовать теорему 10.7.с
заменой числа ![]() числом
числом ![]() :
:
 (34)
(34)
и заметить, что![]() представляет собой конечную сумму
слагаемых вида
представляет собой конечную сумму
слагаемых вида
 .
.
По условию теоремы,
все производные до порядка
![]() включительно непрерывны в окрестности
, поэтому применима теорема 10.6 и, кроме
того,
включительно непрерывны в окрестности
, поэтому применима теорема 10.6 и, кроме
того,
 ,
,
где
![]() .
.
Таким образом,![]() можно
представить в виде
можно
представить в виде ![]()
и суммы конечного
числа слагаемых вида ![]() .Так как
.Так как
![]() и
и![]() ,каждое
слагаемое
,каждое
слагаемое ![]() представляет
собой
представляет
собой  ,
при
,
при
![]() .
.
Это верно и для суммы конечного числа таких слагаемых.◄
