
- •Глава 10. Дифференциальное исчисление функций нескольких переменных
- •§10.1. Дифференцируемость функции многих переменных
- •10.1.1.Определение дифференцируемости функции многих переменных. Частные производные
- •10.1.2. Достаточное условие дифференцируемости функции нескольких переменных
- •§10.2. Дифференциал функции многих переменных и дифференциал отображения
- •10.2.1. Дифференциал функции многих переменных
- •10.2.2 Дифференциал отображения
- •§10.3. Производная сложной функции. Инвариантность формы первого дифференциала. Свойства матрицы Якоби
- •10.3.1. Производная сложной функции
- •10.3.2. Инвариантность формы первого дифференциала
- •10.3.3. Свойства матрицы Якоби. Якобиан
- •§10.4.Геометрические приложения
- •10.4.1. Касательная плоскость
- •10.4.2. Производная по направлению, градиент
- •§10.5.Производные и дифференциалы высших порядков
- •10.5.1. Производные высших порядков
- •10.5.2. Дифференциалы высших порядков
- •10.5.3.Второй дифференциал функции. Матрица Гессе
10.3.3. Свойства матрицы Якоби. Якобиан
Предположим,
что
![]()
![]() и что, в свою очередь,
и что, в свою очередь,![]()
![]() Это приводит к сложному отображению
(или композиции отображений)
Это приводит к сложному отображению
(или композиции отображений)
![]() ,
где
использованы краткие записи
,
где
использованы краткие записи
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() .
.
Для
этого отображения, по теореме о производной
сложной функции,
![]() ,
поэтому
имеет
место равенство:
,
поэтому
имеет
место равенство:
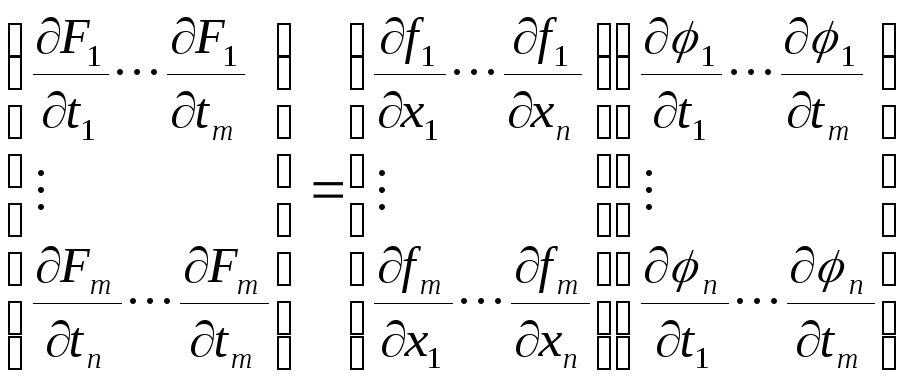 .
.
В
случае, когда
![]() ,
определитель матрицы Якоби
,
определитель матрицы Якоби
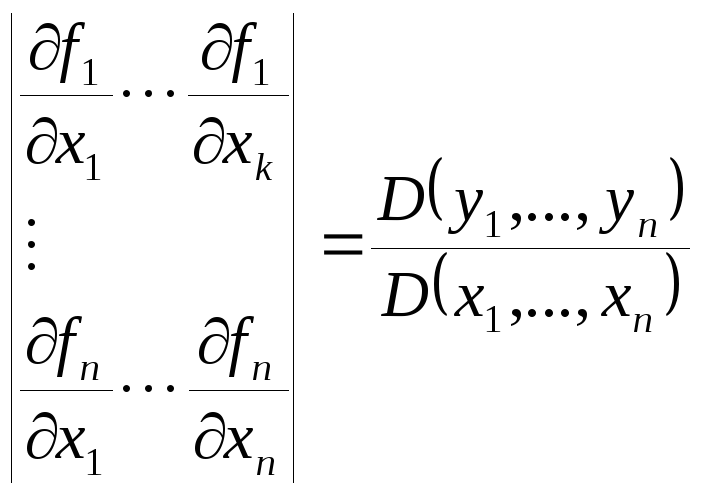 называется
якобианом
отображения.
называется
якобианом
отображения.
По
доказанному, в случае композиции
отображений
![]() ,
,![]() ,
,![]() выполняется
равенство
выполняется
равенство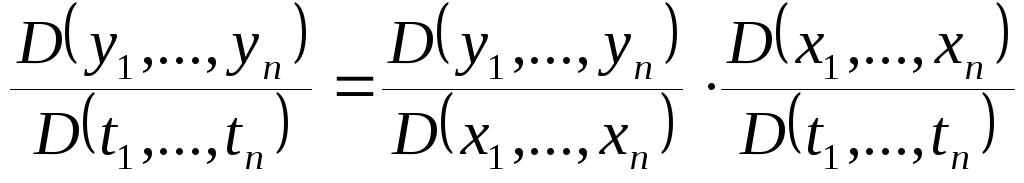 .
Если
отображение
.
Если
отображение
![]() имеет обратное отображение, т.е.
имеет обратное отображение, т.е.
![]() ,
то
,
то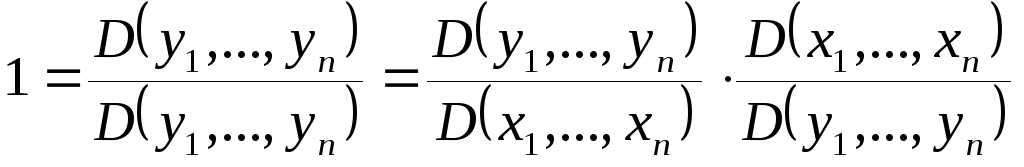 ,
т.е.
,
т.е.
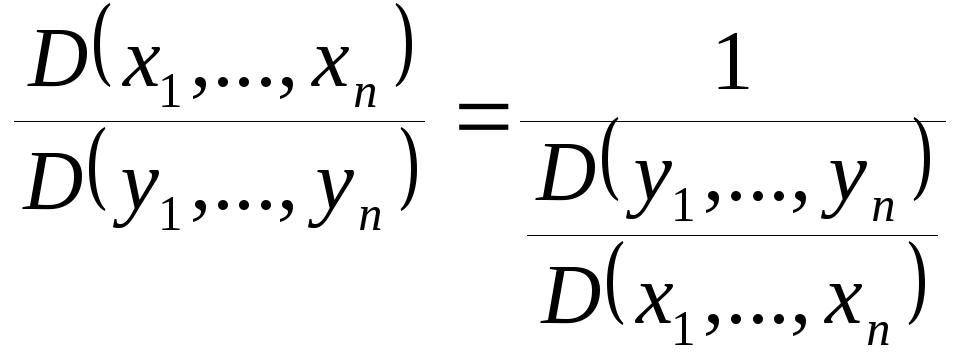 ,
если
,
если
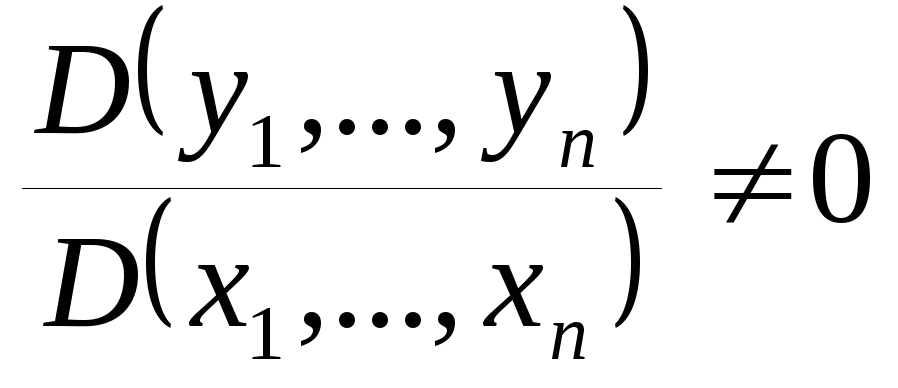 .
Эта
формула обобщает правило для производной
обратной функции :
.
Эта
формула обобщает правило для производной
обратной функции :
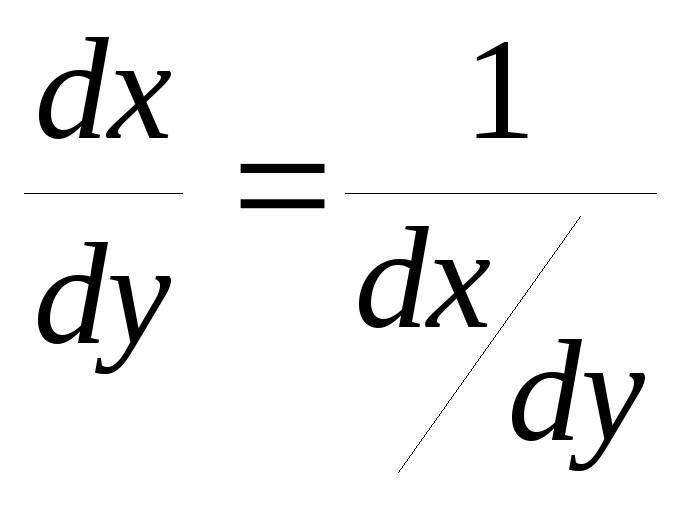 ,
если
,
если![]() .
.
Отметим
важное правило для вычисления якобиана
в случае
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
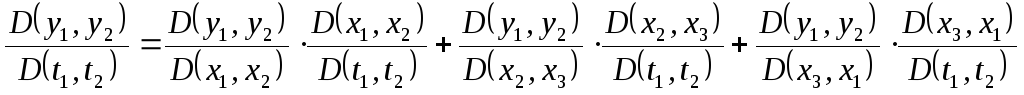 Доказательство этого правила состоит
в применении правила дифференцирования
сложной функции и последующих
алгебраических преобразований. Ввиду
громоздкости мы его опускаем.
Доказательство этого правила состоит
в применении правила дифференцирования
сложной функции и последующих
алгебраических преобразований. Ввиду
громоздкости мы его опускаем.
§10.4.Геометрические приложения
10.4.1. Касательная плоскость
Пусть
![]() дифференцируема в точке
дифференцируема в точке![]() .
Докажем, что существует касательная
плоскость к этой поверхности в точке
.
Докажем, что существует касательная
плоскость к этой поверхности в точке![]() и что она задается уравнением
и что она задается уравнением
![]() .
(14).
.
(14).
По аналогии с
одномерным случаем,( напоминание: прямая
называется касательной
к кривой,
заданной уравнением ![]() в точке
в точке ![]() ,
если расстояние от точки
,
если расстояние от точки
![]() до этой прямой представляет собой
бесконечно малую более высокого порядка,
чем
до этой прямой представляет собой
бесконечно малую более высокого порядка,
чем![]() при
при![]() .
При этом касательная имеет уравнение
.
При этом касательная имеет уравнение![]() ),
будем называть плоскость касательной
к поверхности
в точке
),
будем называть плоскость касательной
к поверхности
в точке
![]() ,
если расстояние от точки
,
если расстояние от точки![]() до этой плоскости есть бесконечно малая
более высокого порядка, чем
до этой плоскости есть бесконечно малая
более высокого порядка, чем![]() при
при![]() .
.
Рассмотрим некоторую
плоскость, проходящую через точку
![]() :
:![]() (15)
(15)
Из курса аналитической
геометрии известно, что расстояние от
точки поверхности
![]() до плоскости (15) равно
до плоскости (15) равно![]() (16)
(16)
(вспомните про нормальное уравнение плоскости).
Если
![]() дифференцируема в точке
дифференцируема в точке![]() ,
то положим в (15)
,
то положим в (15)![]() (17)
(17)
и заметим, что
![]()
![]() ,
(18)
,
(18)
где
![]() при
при![]() .
Тогда из (15)- (18) следует, что расстояние
от рассматриваемой точки до плоскости
есть
.
Тогда из (15)- (18) следует, что расстояние
от рассматриваемой точки до плоскости
есть![]() ,
,
что представляет
собой бесконечно малую более высокого
порядка, чем
![]() .
.
Обратно, если есть
касательная плоскость (15), т.е.
![]() ,
,
где
![]() при
при![]() то, раскрывая модуль, получаем, что
то, раскрывая модуль, получаем, что![]() ,
,
где
![]() при
при![]() ,
т.е.
,
т.е.![]() - дифференцируемая в точке
- дифференцируемая в точке![]() функция и
функция и![]() .
.
10.4.2. Производная по направлению, градиент
Пусть
мы снова рассматриваем график функции
![]() и сечения этой поверхности плоскостями,
проходящими через точку
и сечения этой поверхности плоскостями,
проходящими через точку![]() плоскости OXY и параллельными оси Z. В
сечениях получаются кривые, проходящие
через точку
плоскости OXY и параллельными оси Z. В
сечениях получаются кривые, проходящие
через точку![]() .
Проекция такой кривой на плоскость OXY
есть прямая линия, проходящая через
точку
.
Проекция такой кривой на плоскость OXY
есть прямая линия, проходящая через
точку![]() .
Будем
обозначать направляющий вектор этой
прямой через
.
Будем
обозначать направляющий вектор этой
прямой через
![]() ,
а точки прямой – буквами
,
а точки прямой – буквами![]() .
Введём понятие величины отрезка
.
Введём понятие величины отрезка
![]() :
:
![]() длине
отрезка
длине
отрезка
![]() со знаком “+”, если
со знаком “+”, если![]() и
и![]() имеют одинаковые направления;
имеют одинаковые направления;
![]() длине
отрезка
длине
отрезка
![]() со знаком “-”, если
со знаком “-”, если![]() и
и![]() имеютразные
направления;
имеютразные
направления;
Предположим
теперь, что мы рассматриваем некоторую
плоскость, на ней фиксируем точку
![]() и направление
и направление![]() .
Пусть для этой точки плоскости определена
величина
.
Пусть для этой точки плоскости определена
величина![]() - функция от точки
- функция от точки
![]() .
.
Важно отметить, что пока мы не вводим никакой системы координат (точки на плоскости, направления и функции от точек можно определить без системы координат). Например, температуру воздуха в данной точке обычно просто измеряют термометром, не задумываясь о системе координат в пространстве. Направление тоже часто указывают, не вводя координаты.
Рассмотрим
теперь точки ![]() , лежащие на прямой, проходящей через
, лежащие на прямой, проходящей через
![]() в указанном направлении
в указанном направлении![]() и соответствующую величину
и соответствующую величину![]() ;
если существует предел этой величины
при стремлении
;
если существует предел этой величины
при стремлении![]() к
к
![]() вдоль прямой, то он называется производнойфункции
вдоль прямой, то он называется производнойфункции
![]() в точке
в точке
![]() по направлению
по направлению![]() и обозначается
и обозначается![]() .
Как
мы видим, в определении производной по
направлению координаты не участвовали.
Однако для получения простой формулы
для вычисления этой производной удобно
ввести систему координат. Итак, пусть
.
Как
мы видим, в определении производной по
направлению координаты не участвовали.
Однако для получения простой формулы
для вычисления этой производной удобно
ввести систему координат. Итак, пусть
![]() имеет координаты
имеет координаты![]() ,
,
![]() – координаты
– координаты
![]() ,
,![]() имеет координаты
имеет координаты![]() .
Тогда вводя параметризацию
.
Тогда вводя параметризацию![]() ,
,![]() ,
для прямой, соединяющей
,
для прямой, соединяющей![]() с
с![]() , получаем:
, получаем:
![]()
(т.
к.
мы предположили, что
![]() – дифференцируема в
– дифференцируема в![]() )
)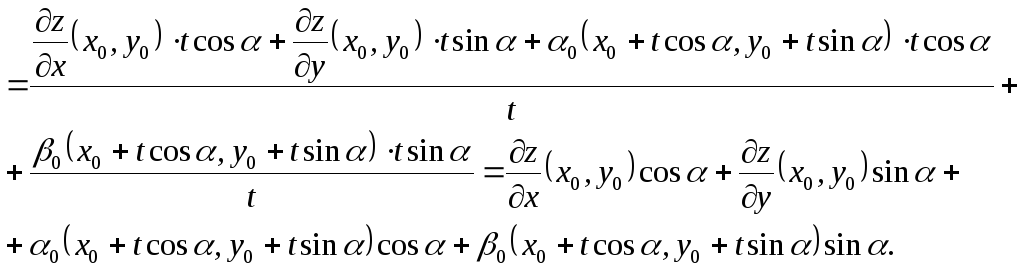
При
![]()
![]() и
и![]() .
Поэтому
.
Поэтому![]() (19)
(19)
Аналогично,
в случае 3-х переменных
![]() (20)
(20)
Скалярное
произведение в правых частях (19)
или (20)
можно представить, как
![]() (поскольку
(поскольку
![]() ),
где
),
где![]() - угол между
- угол между![]() и заданным направлением
и заданным направлением
![]() .
.
Мы
видим, что выражение![]() имеет наибольшую величину, когда
имеет наибольшую величину, когда![]() .
Это позволяет определить градиент, как
вектор, модуль которого равен наибольшей
из величин
производных
по направлению в этой точке. А направление
его как раз такое, в котором производная
по направлению
достигает
наибольшей величины. Это определение
градиента, в котором не участвуют
координаты, позволяет рассматривать
его как характеристику функции, не
зависящую от наблюдателя.
Вместе с тем, выражение градиента через
координаты удобно при его вычислении.
.
Это позволяет определить градиент, как
вектор, модуль которого равен наибольшей
из величин
производных
по направлению в этой точке. А направление
его как раз такое, в котором производная
по направлению
достигает
наибольшей величины. Это определение
градиента, в котором не участвуют
координаты, позволяет рассматривать
его как характеристику функции, не
зависящую от наблюдателя.
Вместе с тем, выражение градиента через
координаты удобно при его вычислении.
Установим ряд важных свойств градиента.
Теорема 10.4.
Пусть
![]() и
и![]() имеют все частные производные 1-го
порядка. Тогда
имеют все частные производные 1-го
порядка. Тогда
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
Если
![]() ,
то
,
то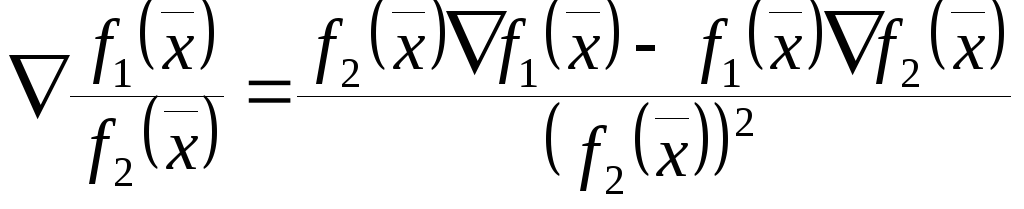 ;
;
5.
Если
![]() - функция одной переменной, имеющая
производную, то
- функция одной переменной, имеющая
производную, то![]() .
.
►Доказательства
всех этих свойств аналогичны. Разберем,
например, свойство 3. Пусть, для
определенности,
![]() .
Тогда, по правилам дифференцирования,
.
Тогда, по правилам дифференцирования,
![]() и
и
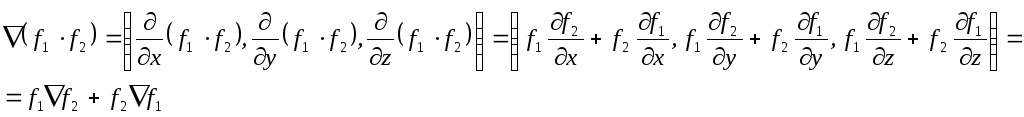 .◄
.◄
Пусть
![]()
![]() .
Найдём
.
Найдём![]() .
.
Для
часто встречающихся в физике радиальных
функций
![]() согласно свойству 5
получаем:
согласно свойству 5
получаем:
![]() .
.
