18

Глава 10. Дифференциальное исчисление функций нескольких переменных

§10.1. Дифференцируемость функции многих переменных

10.1.1.Определение дифференцируемости функции многих переменных. Частные производные

Пусть определена в некоторой окрестности точки,- точка из этой окрестности.

Определение. Величина называетсяприращением функции в точке,соответствующим приращению аргумента.

Определение. Функция называетсядифференцируемой в точке , если существуют такие постоянные числаи функциипри(1)

Часто обозначают и. Тогда (1) перепишем в виде.

При наше определение (1) совпадает с известным определением дифференцируемости(пункт 6.1.1). Для функций одной переменной дифференцируемость равносильна существованию производной( теоремы 6.2 и 6.3). В случае нескольких переменных ситуация несколько сложнее.

Сначала введем в рассмотрение величину . Она представляет собой приращение функции при фиксированных значениях всех производных, кромеi-той.

Пусть дифференцируема в точке. Тогда для любогоравенство (1) дает

при (2)

Поскольку при фиксированных значенияхравносильно тому, что, равенство (2) означает, что функцияодной переменнойдифференцируема в точкеи, значит, существует предел (3) называемый, по определению, частной производной функции по переменнойв точке.

Мы только что, тем самым, доказали теорему:

Теорема 10.1. Если дифференцируема в точке, то для всехсуществуют.

Таким образом, существование частных производных – необходимое условие дифференцируемости. При этом

при .

Другое необходимое условие дифференцируемости – непрерывность функции, как показывает следующая теорема.

Теорема 10.2. Если дифференцируема в точке, то.

►Достаточно доказать, что при ,, (т.к.). Но это сразу следует из равенства (1), так как. ◄

Однако, в отличие от случая , из существования частных производных,определенных равенством (3) не следует даже непрерывность функциив точкеи тем более не следует дифференцируемостьв точке, согласно теореме10.2.

Пример. Тогда , так как. Аналогично,. Однакодаже не непрерывна в точке.

10.1.2. Достаточное условие дифференцируемости функции нескольких переменных

Достаточное условие дифференцируемости дает следующая теорема.

Теорема 10.3. Пусть частные производные существуют в окрестности точкии непрерывны в этой точке. Тогдадифференцируема в точке.

► Рассмотрим сначала простой случай .

Пусть точки ипринадлежат рассматриваемой окрестноститочки. Рассмотрим приращение функции в точке:и представим его в виде:

.

Зафиксировав , рассмотрим функцию от переменнойвида

.

Поскольку в существуют частные производные, функциядифференцируема на любом промежутке, содержащеми. Применим поэтому теорему Лагранжа, согласно которой

, где .

По определению частной производной,

.

Поэтому

.

Аналогичным образом,

.

Следовательно,

.

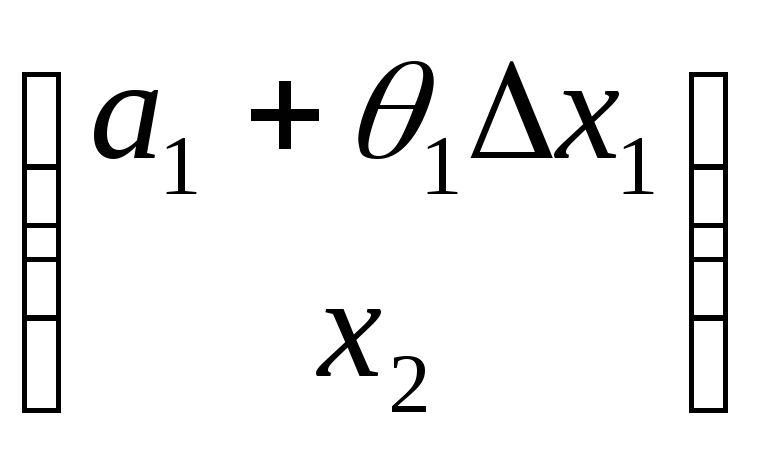Далее, при →точкии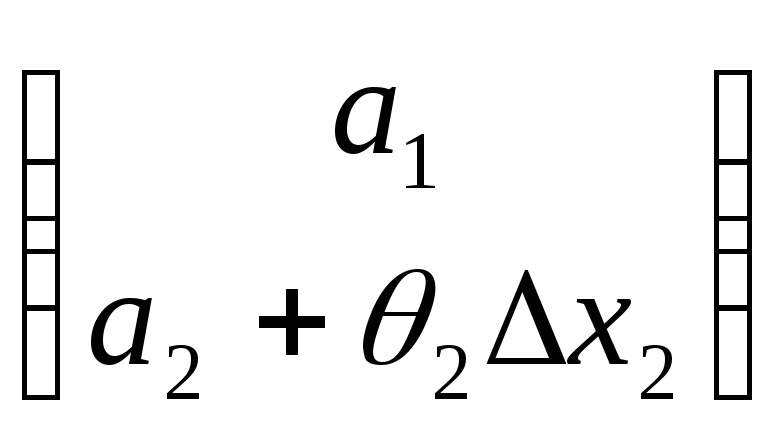стремятся к точке.

Непрерывность частных производных в этой точке означает, что их можно представить в виде

,

, где при→.

Поэтому получаем представление для приращения функции:

,

означающее дифференцируемость функции .Случайрассмотрен.

В общем случае пусть принадлежит рассматриваемой окрестности. При этом все точкитак же принадлежат рассматриваемой окрестности. Приращение функциипредставим в виде

(4)

и рассмотрим разности

, (5)

составляющие в сумме приращение (4).

Положим (то есть фиксируем все переменные, кроме). Тогда рассматриваемая разность (5) имеет вид. Функцияпо условию дифференцируема на отрезке, соединяющеми. Значит, она непрерывна на этом отрезке и можно применить теорему Лагранжа, согласно которой, где. Но. По условию непрерывности частных производных, гдепри.

Поэтому каждая из разностей (5) имеет вид , а приращение (4) совпадает с (3) из определения дифференцируемости. ◄

Замечание. Непрерывность частных производных не является необходимым условием дифференцируемости функций. Например можно доказать, что функция 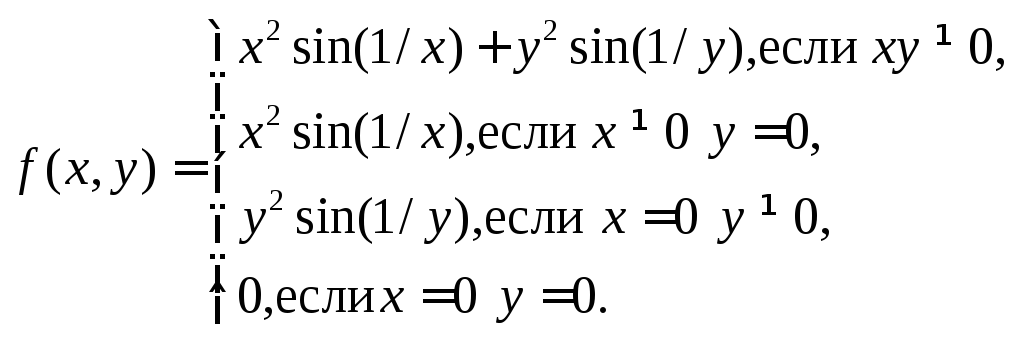дифференцируема в точке , но частные производные в этой точке не непрерывны.

Замечание. Тем не менее, для функции частные производные в точкеравны 0, так каки(в остальных точках,и ясно, что эти производные терпят разрыв в точке. Но функция не дифференцируема в точке (0,0) , так как её приращениене имеет вида

, где при. Действительно, полагаяи предполагая, что,

получаем , иличто невозможно, так как приправая часть стремится к 0, а левая нет!