Изучение свойств последовательного и параллельного колебательных lc – контуров

Цель работы: Изучение резонансных и фильтрующих свойств параллельного и последовательного контуров, измерение их основных параметров, снятие частотных и переходных характеристик. Компьютерное моделирование лабораторного эксперимента.

1. Свободные колебания в lc – контуре

Простой и широко используемой в радиоэлектронике линейной системой является колебательный контур. Он содержит конденсатор С, индуктивность L и сопротивление R. Пусть в момент времени t=0 на конденсаторе имеется заряд q_o = CU_o. Найдем закон изменения во времени заряда на конденсаторе.



L

С

R

На основании второго закона Кирхгофа:

.

Учитывая, что , и вводя обозначения(- коэффициент затухания,- собственная циклическая частота контура), получим:

Если », решение уравнения может быть представлено в виде:

, где .

Таким образом, при »зависимость величины заряда на конденсаторе от времени имеет характер затухающих колебаний, частота которых несколько меньше собственных колебаний контура. Учитывая начальные условияt = 0, q = q₀ , при »можно считать:.

Закон изменения силы тока i = q₀ω₀e^-αtcos(ω₀t + π/2).

Зная, что q₀ = CU₀ и ω₀ = , получим:

.

Следовательно, ток в цепи также совершает затухающие колебания, начальная амплитуда которых . Величина, имеющая размерность сопротивления, называется характеристическим (волновым) сопротивлением контура. Волновое сопротивление контура – это индуктивное или емкостное сопротивление току резонансной частоты:

.

Кроме коэффициента затухания , используют логарифмический декремент затухания:

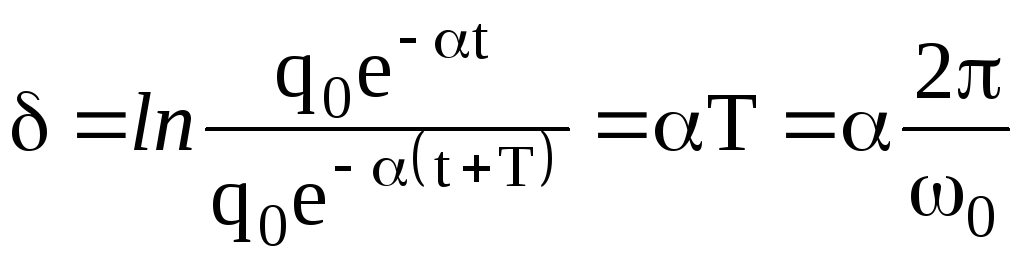
Величина обратная ,, определяет число периодов, за которое амплитуда колебаний убывает в е раз.

Важным параметром колебательного контура является добротность, характеризующая относительную убыль энергии в процессе колебаний.

Энергия, запасенная колебательной системой, равна максимальной энергии, накопленной конденсатором или катушкой индуктивности:

Энергия, теряемая в контуре за период колебаний, равна:

,

где R – активное сопротивление, определяющее полную мощность Р, теряемую в цепи:

Используя эти положения, получим выражение для добротности:

.

2. Вынужденные колебания в последовательном контуре

Подключим контур к источнику гармонического сигнала с амплитудой E_m с начальной фазой φ_e

L

^

e C

R

Тогда дифференциальное уравнение примет вид:

Воспользовавшись методом комплексных амплитуд дифференциальное уравнение можно представить в виде:

,

откуда следует, что

Это есть закон Ома для последовательного колебательного контура. - импеданс последовательного контура. Зная, что, модуль полного комплексного сопротивления будет иметь вид:

,

а фаза: .

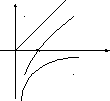
На рис. 1 приведена частотная зависимость реактивного сопротивления последовательного контура.

X_c X ωL

Из условия (ωL – 1/ωC) = 0

X=ωL – 1/ωC определяется резонансная

частота контура.

ω_o ω

1/ωC

Рис. 1

Последовательный колебательный контур есть линейный четырехполюсник:



L

U_вх C U_вых

R

Комплексный коэффициент передачи такой системы:

.

Представив его в показательной форме, получим

.

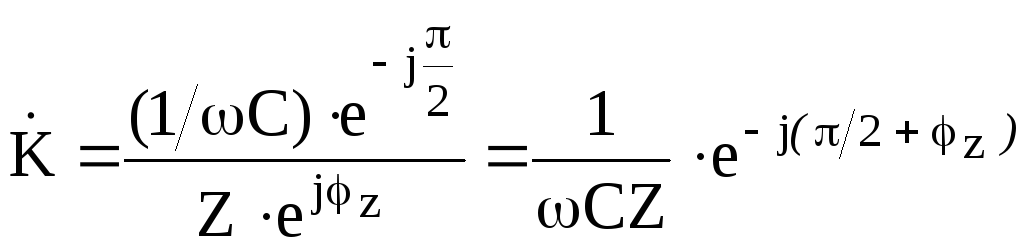Модуль комплексного коэффициента передачи и его фаза примут вид ,.

Выражение K=1/ωCZ – есть амплитудно-частотная характеристика, а φ_к(ω) – фазово-частотная характеристика контура. Для определения этих выражений найдем модуль и аргумент коэффициента передачи в узкой полосе частот в окрестностях резонансной частоты контура ω_о.

Пусть ω = ω_о + Δω, Δω « ω_о. Введем понятие (ω – ω_о)/ω = Δω/ω_о = ξ – относительная расстройка контура.

Учитывая эти понятия, получим для

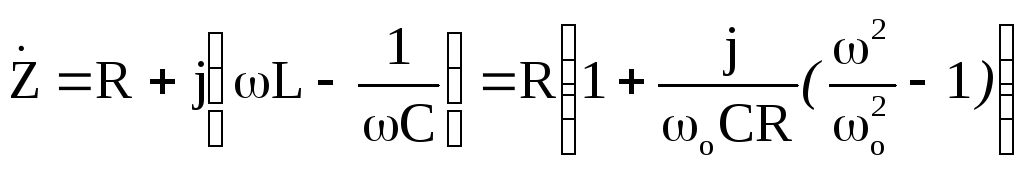
Полагая, что , а, получим

, откуда

Подставим Z и φ_z (ω) в выражение для K и φ_к (ω).

,

Амплитудно-частотная и фазово-частотная характеристики последовательного колебательного контура приведены на рис. 2.

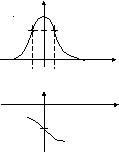K=Q_о Без учета сопротивления ис-

точника сигнала при ξ = 0

K_гр=K/(ω = ω_o) модуль -

добротности. Полоса пропус-

кания контура как полосового

-_гр. _гр.  фильтра при

_к определится выражением

ξ

-π/2

Рис. 2.

Или, переходя к частоте f, выражение для полосы пропускания примет вид Δf_пр = f_o / Q_o.

В реальной ситуации сопротивление генератора R_г не является нулевым и внесет вклад в формулу добротности:

.

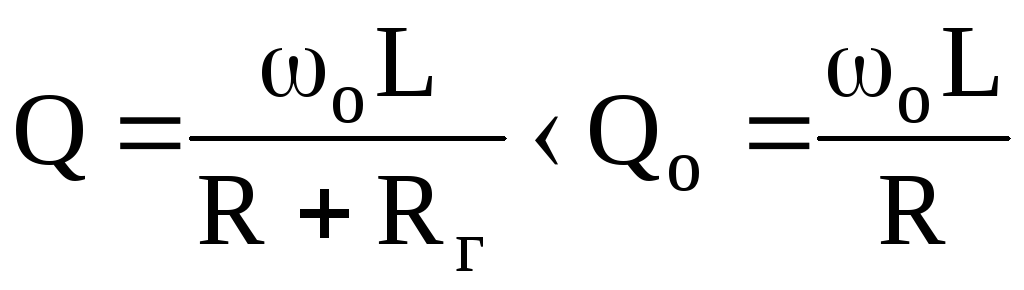Следовательно, для получения или сохранения высокого значения добротности системы сопротивление генератора не следует делать большим.