
физика
.pdfУказания к решению задач по механике.
При решении задач по кинематике следует:
1. Определить характер движения тела (равномерное, неравномерное,
прямолинейное, криволинейное и т.д.;
2.Определить начало отсчета времени;
3.Выбрать систему и начало координат;
4. Записать уравнение в общем виде, например: S S0 t;
5. Записать уравнение в общем виде в проекциях на оси координат.
Например: x x0 xt
При решении задач на второй закон Ньютона нужно использовать следующие общие правила:
1.изобразить схематически тело и указать все действующие на него силы и кинематические величины;
2.выбрать тело отсчета и инерциальную систему отсчета (одну из осей декартовой системы координат обычно проводят в направлении движения тела;
3.указать начало координат и начало отсчета времени;
4.для каждого тела записать уравнение второго закона Ньютона
применительно к условиям задачи |
ma F F |
... F |
|
1 2 |
n |
5. заменить векторные уравнения скалярными, спроецировав все векторы
на оси координат: |
max |
F1x F2x ... Fnx |
|
may |
F1y F2y ... Fny |
6. решить полученное уравнение относительно искомой величины.
Движение тел под действием силы тяжести по вертикали.
Данное движение рассматривается как частный случай равнопеременного движения, но с определенным для всех случаев ускорением свободного падения g = 9,8 м/с2 (для упрощенных расчетов принимают g = 10 м/с2). В задачах используют формулы равнопеременного движения, направляя ось y или x вертикально вверх и обозначая высоту буквой h.
Механическая энергия.
При решении задач по данной теме нужно обратить внимание на то,
что значение потенциальной энергии определяют относительно уровня,
условно принимаемого за нулевой. Обычно это уровень поверхности земли.
Указания к решению задач по электродинамике.
При решении задач необходимо учитывать следующее:
1.Если не указывается относительная диэлектрическая проницаемость среды, подразумевается, что электрические заряды взаимодействуют в вакууме или в воздухе.
2.Относительная диэлектрическая проницаемость вакуума, воздуха считается равной единице (ε= 1).
3.Там где требуется по условию задачи, приводить рисунок или схему физического процесса.
4.При вычислении модулей сил взаимодействия зарядов по закону Кулона знаки зарядов не учитывают.
5.При решении задач на соединение резисторов следует:
а) все точки соединения или разветвления в схемах обозначить буквами, а
сопротивления участков – буквенными индексами, например RAB, RCD и
т.д.;

б) вместо сложных схем соединения начертить так называемые эквивалентные схемы, в которых видны все точки разветвления и характер соединения отдельных участков цепи;
в) расчеты в общем виде в большинстве случаев проводить не следует.
Удобнее вначале определить сопротивление каждого участка цепи, а затем уже – сопротивление цепи в целом.
7. В случае замкнутой электрической цепи силу тока определяют по закону Ома для полной цепи. В задачах обычно принимают, что у источника тока ε = const, r = const.
И, наконец, НЕ забывайте переводить числовые значения физических величин в систему Си.
Примеры решения типовых задач.
1. Автомобиль проехал первую половину пути со скоростью 20 м/с, а вторую половину со скоростью 30 м/с. Найдите среднюю скорость автомобиля на всем пути.
Дано: S1=S2 = |
|
S |
; |
|
υ1 = 20 м/с; |
|
υ2 = 30 м/с. |
|
||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти υср. - ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
υср.= |
S |
|
(1); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Полное время t |
прохождения пути S: |
|||||||||||||||||||||||
t = t1 + t2 |
= |
S |
|
|
|
|
S |
|
|
S |
|
1 |
|
1 |
|
S |
|
1 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 1 |
2 2 |
|
|
|
1 |
|
2 |
1 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||||||||||
υср. = |
|
|
|
S |
|
|
|
|
|
2 1 2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
υср. = 2*20*30 24 м/с 20 30

2. Частота вращения воздушного винта самолета 1500 об/мин. Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч?
Дано: S = 90 км = 9*104 м; υ = 180 км/ч = 50 м/с; ν =1500 об/мин = 25 об/с.
Найти: N - ?
Решение: Определим время движения самолета t= S/υ.
Период обращения винта самолета равен Т = 1 .
Число оборотов за время движения самолета t определяем по
формуле N = |
t |
= |
S |
. |
N = |
9*104 *25 |
4,5*104 (оборотов) |
|
T |
|
|
50 |
|
||
3. Камень, свободно падая с некоторой высоты, имел в конце падения скорость 50 м/с. С какой высоты падал камень?
Дано: υк = 50 м/с. Найти h.
Решение: y = y0 + υ0yt + |
|
g |
y |
*t2 |
; |
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
В нижней точке 0 = h - |
g*t2 |
; |
h = |
g*t2 |
. |
(1) |
|||
|
|
2 |
|
|
|||||
|
|
|
|
|
2 |
|
|
||
υу = υ0у + gyt; тогда скорость в нижней точке -υк = -g t.
Время падения t = к . g
Подставим его значение в (1) и получим:
h = |
g к2 |
|
к2 |
. |
h = |
502 |
125 м. |
|
|||||||
|
2g2 |
|
2g |
2*10 |
|
||
4. Определите силу тока в электрической цепи при нагрузке сопротивлением 6 Ом, если ЭДС источника равна 8 В, а его внутреннее сопротивление 0,4 Ом. Чему равны падения напряжения на внешнем и внутреннем участках цепи?
Дано: R = 6 Oм; ε = 8 В; r = 0,4 Ом.

Найти: U1 - ? U2 - ?
Решение: Запишем закон Ома для общей цепи ε = I (R +r)
Следовательно I = |
|
I = |
8 |
|
8 |
1,25 A |
|
R r |
6 0,4 |
6,4 |
|||||
|
|
|
|
Тогда U1 = IR = 1,25*6 = 7,5 B.
U2 = Ir = 1,25*0,4 = 0,5 B.
5. Величину каждого из двух одинаковых точечных зарядов уменьшили в 10 раза, а расстояние между ними уменьшили в 4 раза. Найдите отношение конечной силы их взаимодействия к начальной.
Решение. Сила взаимодействия между точечными зарядами определяется по закону Кулона:
F = k q1 
 q2 r2
q2 r2
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
q2 |
|
|
|
|
|
|
|
q1 |
|
|
|
|
|
q2 |
|
|||||||
Было: |
|
|
F1 |
= k |
|
|
|
|
|
|
|
|
Стало: |
F2 = k |
|
|
|
10 |
|
|
|
|
|
|
10 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
r2 |
|
|
|
|
|
|
r 2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||||||
F |
|
|
q1 |
|
q2 |
|
|
|
|
|
q1 |
|
|
|
|
|
q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k |
|
|
|
: k |
|
10 |
|
|
|
|
|
10 |
|
= 6,25 раз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F2 |
|
|
r2 |
|
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6. Тело массой 3 кг свободно падает с высоты 5 м. Найти потенциальную и кинетическую энергию тела на расстоянии 2 м от поверхности земли.
Дано: m = 3 кг; h = 5 м. Найти ЕП и ЕК.
Решение: Запишем закон сохранения энергии.
|
EП1 = ЕП2 + ЕК2 |
|
|||
или |
mgh1 |
= mgh2 |
+ |
m 22 |
, |
|
|||||
|
|
|
2 |
|
|
так как ЕК1 = 0, то ЕК2 = mgh1 – mgh2 = mg(h1 – h2)
EК2 = 3*10*3 = 90 Дж.
EП2 = mgh1 - m 22 = 3*10*5 – 3*10*3 = 60 Дж
2
7. Определите модуль и направление силы, действующей на проводник длиной ℓ = 0,2 м при силе тока I = 10 А в магнитном поле с индукцией В =
0,13 Тл, если угол α между В и ℓ равен : а) |
900; |
б) 300. |
Дано: ℓ = 0,2 м; I = 10 А; В = 0,13 Тл. α а) |
900; |
б) 300. |
Найти: F. |
|
|
Решение: а) При α = 900 sin 900 = 1, тогда F1 = BI ℓ ≈ 0,26 H.
б) При α = 300 sin 300 = 0.5. поэтому F2 = BIℓ sin 300 = 0,13 H.
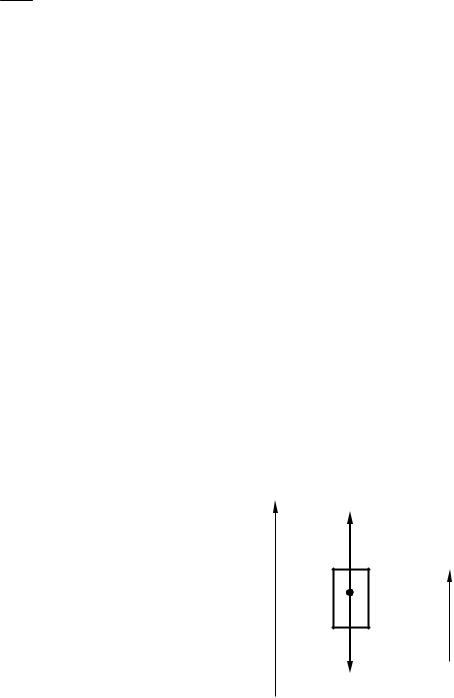
8. Какую работу совершает человек при поднятии груза массой 5 кг на высоту 3 м с ускорением 3 м/с2?
Дано: m = 5 кг; h = 3 м; а = 3 м/с2.
Найти: А -?
Решение: На тела действуют две силы: сила тяжести mg и сила человека F , под y действием которых груз поднимается с ускорение a. Запишем второй закон Ньютона в векторной форме:
ma mg Fч.
Но действия мы производим не с векторами, а с проекциями сил на координатные оси.
Fч
а
mg
В проекциях на ось 0х имеем:
ma = F – mg, |
(1), |
следовательно, сила, с которой необходимо тянуть человеку груз вверх будет равна
F = m(a+g). |
(2) |
Тогда работа при перемещении груза на высоту h,
A = Fч.h = m(a + g)h.
A = 5 *3*(3 + 9,8) ≈ 192 (Дж).
9. Троллейбус, масса которого 12 т, за 5 с проходит по горизонтальному пути 10 м. Определите силу тяги, развиваемую двигателем, если сила трения 2,4 кН.
Дано: m = 12 т = 12*103 кг; υ0 = 0; t = 5 c; S = 10 м; Fтр. = 2,4 кН = 2,4*103 Н.
Решение:
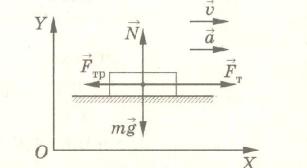
На тело действуют четыре силы: mg – сила тяжести, N - сила реакции опоры;
F тр. – сила трения, F - сила тяги, рис. . Запишем уравнение второго закона Ньютона в векторной форме:
ma mg N Fтр. Fт.
За положительное направление оси Х примем направление движения троллейбуса.
Запишем уравнение движения в проекции на ось Х:
ma Fт Fтр. |
(1) |
Ускорение определим из формулы
S |
at2 |
; |
a |
2S |
(2) |
|
t2 |
||||
2 |
|
|
|
||
Из уравнения (1) находим, что Fт ma Fтр.
Подставим значение ускорения из уравнения (2), получим:
2S
Fт m t2 Fтр.
Подставим числовые значения, получим:
F = 12*103*2*10 + 2?4 *103 = 12*103H = 12 кН.
т |
25 |
|
Ответ: Fт. = 12 кН.
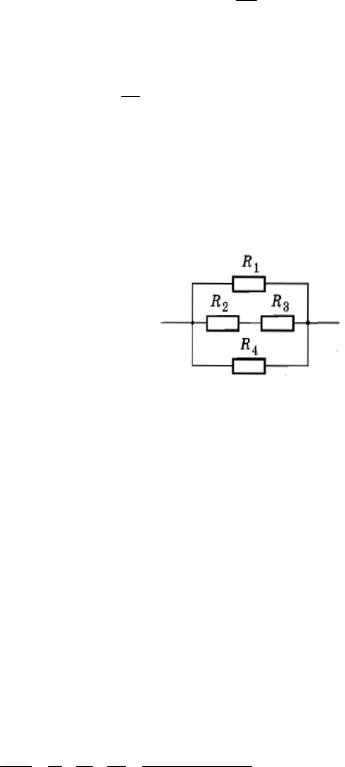
10. Вычислите общее сопротивление участка цепи, изображенного на рисунке, если R1 = 2 Ом, R2 = 3 Ом, R3 = 5 Ом,R4 = 20 Ом.
Решение.
Цепь состоит из двух последовательно включенных проводников R2 и R3.
Сопротивление R двух последовательно соединенных сопротивлений R2 и R3 равно:
R = R2 + R3 = 3 + 5 = 8 (Ом).
В свою очередь сопротивления R1, R4 и R соединены параллельно друг с другом.
1 1 1 1 R1R4 RR4 RR1
Rобщ. R R1 R4 RR1R4
или |
R |
R*R1 *R4 |
|
R1R4 RR4 RR1
Подставляем числовые значения.
Ответ: Rобщ. = 1,48 Ом.
11. Через сколько времени после начала торможения остановиться автомобиль, если его начальная скорость 15 м/с, а коэффициент трения 0,4.
Дано: υ0 = 15м/с, μ = 0,4.
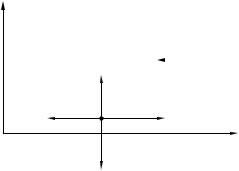
Решение:
На тело действуют три силы: сила y трения, сила реакции опоры и сила тяжести. Запишем второй закон Ньютона
а
N
в векторной форме.
Fтр |
|
Fт |
ma N mg Fтр. |
|
x |
|
||
|
|
Теперь найдем проекции этих сил на |
|
|
|
|
|
|
mg |
|||||||||||
координатные оси: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0х: ma Fтр. |
или |
|
ma Fтр. |
(1) |
|
|
|||||||||
|
|
|
0y: 0 N mg |
или |
|
N mg |
|
|
|
|||||||||
Тогда сила трения Fтр. mg |
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|||
Подставляем (2) в (1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Имеем: |
|
|
ma mg; или |
|
a mg |
|
|
|
||||||||||
Из кинематики нам известно, |
что |
|
|
|
|
|
a |
0 |
, |
но по условию задачи |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
конечная скорость υ=0. Тогда |
a |
0 |
|
|
0 |
; следовательно a |
0 |
. |
||||||||||
|
|
|||||||||||||||||
|
|
t |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
t |
|||||||
Откуда |
t |
0 |
, но a mg , поэтому t |
0 |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a |
|
|
mg |
|
|
|
|
|
|
|
|
|
||||
Подставляем числовые значения t |
15 |
|
3,75 (с). |
|||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
0,4*9,8 |
|
|
|
|
|
|
|
|
|||||
Ответ: |
t 3,75 (с). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Основные физические постоянные
Ускорение свободного падения |
g = 9,8 м/с2 |
(Земля) |
|
|
|
Гравитационная постоянная |
6,67*10-11 Н*м2/кг2 |
|
|
Масса Земли |
Mз = 6*1024 кг |
|
|
Радиус Земли |
Rз = 6400 км |
|
|
Масса Луны |
Mл = 7,35*1022 кг |
|
|
Радиус Луны |
Rл = 1740 км |
|
|
Скорость света в вакууме |
с = 3*108 м/с |
|
|
Магнитная постоянная |
μ0 = 4π*10-7 Гн/м |
|
|
Электрическая постоянная |
ε0 = 8,85 *10-12 Ф/м |
|
|
Масса покоя электрона |
me = 9,1*10-31 кг |
|
|
Масса покоя протона |
mp = 1,67*10-27кг |
|
|
Заряд электрона |
e = 1,6*10-19 Кл |
|
|
Электрон-вольт |
1эВ = 1,6*10-19 Дж |
|
|
Коэффициент пропорциональности |
k = 9*109 Н*м2/Кл2 |
|
|
