
- •4. Блок контроля освоения дисциплины
- •4.1. Методические указания к выполнению контрольных работ
- •4.1.1. Методические указания к выполнению контрольной работы № 5 Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Линейные дифференциальные уравнения
- •Степенные ряды
- •4.1.2. Методические указания к выполнению контрольной работы № 6 Двойные интегралы
- •Криволинейные интегралы
- •4.2. Задания на контрольные работы № 5 и №6
- •Контрольная работа №5
- •Контрольная работа №6
- •4.3. Блок тестов текущего контроля Тренировочные тесты Тест №1
- •Тест №2
- •Тест №3
- •Тест №4
- •Тест №5
- •Тест №6
- •Тест №7
- •Тест №8
- •Тест №9
- •Тест №10
- •4.4. Блок итогового контроля
- •4.4.1. Вопросы для подготовки к экзамену по 3-му семестру
- •4.4.2. Список типовых задач для подготовки к экзамену
Тест №9
1. Используя теорему Вейерштрасса, выяснить вопрос о равномерной сходимости функционального ряда
![]()
1) ряд равномерно сходится при всех x; 2) ряд расходится при всех x;
3)
ряд равномерно сходится только при
![]() ;
;
4)
ряд расходится при
![]() ;
;
2. Исследовать область сходимости степенного ряда

1) ряд сходится абсолютно и равномерно в интервале [-5,3];
2) ряд сходится абсолютно и равномерно в интервале (-5,3);
3) ряд сходится абсолютно и равномерно в интервале (-3,1);
4) ряд сходится абсолютно и равномерно в интервале [-3,1].
3.
Найти область сходимости и радиус
сходимости степенного ряда
 .
.
1)
ряд сходится
абсолютно и равномерно в интервале
[-4,-2], радиус сходимости равен
![]() ;
;
2)
ряд сходится абсолютно и равномерно в
интервале (-4,-2), радиус сходимости равен
![]() ;
;
3)
ряд сходится абсолютно и равномерно в
интервале (-1,1), радиус сходимости равен
![]() .
.
4)
ряд сходится абсолютно и равномерно в
интервале [1,1], радиус сходимости равен
![]()
4.
Написать
разложение в ряд Тейлора функции
 в окрестности точки
в окрестности точки![]() .
.
1)
 ;2)
;2)
 ;3)
;3)
 .
.
5.
Разложить
в ряд Маклорена функцию
![]() .
.
1)
 ,
-∞<x<∞;
2)
,
-∞<x<∞;
2)
 ,
|x|<1;
3)
,
|x|<1;
3)
 ,
|x|<1.
,
|x|<1.
Тест №10
Определите, чему равен
 ,
не вычисляя его, если
,
не вычисляя его, если -
область, ограниченная координатными
осями и прямой
-
область, ограниченная координатными
осями и прямой .
.
1) 4; 2) 8; 3) 16; 4) 0.
 Выберите
повторный интеграл, к которому сведется
двойной интеграл
Выберите
повторный интеграл, к которому сведется
двойной интеграл
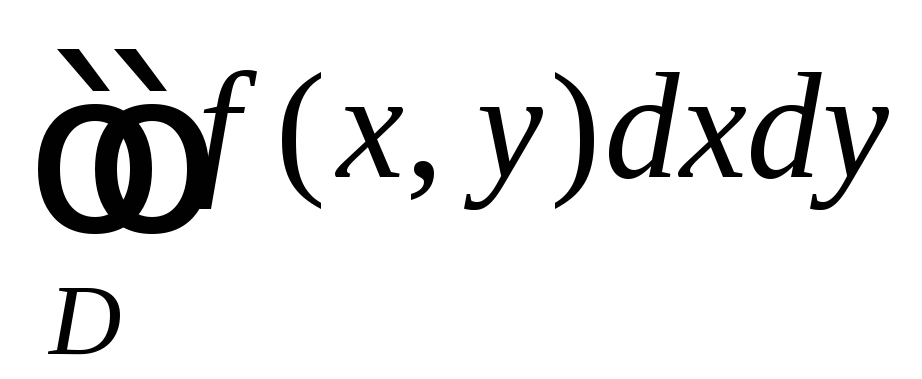 по области
по области ,
заштрихованной на рисунке.
,
заштрихованной на рисунке.
1)
 ;
;
2)

3)
 ;4)
;4)
 .
.
3 .
Выберите повторный интеграл, к которому
сведется двойной интеграл
.
Выберите повторный интеграл, к которому
сведется двойной интеграл при переходе к полярным координатам.
Область
при переходе к полярным координатам.
Область![]() заштрихована на рисунке.
заштрихована на рисунке.
1)
 ;2)
;2)
 ;
;
3
Рис. 6.17 ;4)
;4)
 .
.
4.
Вычислите
 ,
где
,
где![]() - область, ограниченная осями координат,
прямой
- область, ограниченная осями координат,
прямой![]() и кривой
и кривой![]() .
.
1)
 ;2)
;2)
![]() ;3)
;3)
 ;4)
;4)
![]() .
.
5.
Переходя к полярным координатам,
вычислите
 ,
где область
,
где область![]() задается неравенствами:
задается неравенствами:![]() .
.
1)
0; 2)
![]() ;3)
2; 4)
4.
;3)
2; 4)
4.
Тест №11
Найдите дифференциал
 длины дуги кривой
длины дуги кривой .
.
1)
![]() ;2)
;2)
![]() ;3)
;3)
![]() ;4)
;4)
![]() .
.
Найдите дифференциал длины дуги кривой
 .
.
1)
![]() ;2)
;2)
![]() ;
;
3)
![]() ;4)
;4)
![]() .
.
Найдите массу дуги материальной кривой
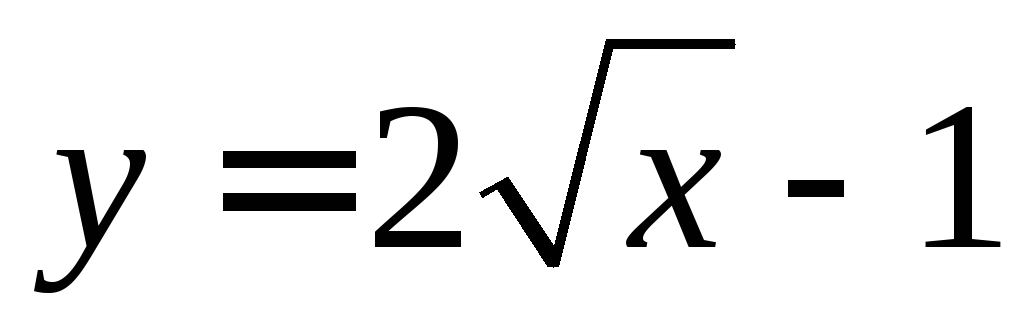 между точками
между точками
 и
и ,
если плотность вещества
,
если плотность вещества .
.
1)
4;
2)
1; 3)
![]() ;4)
;4)
 .
.
Вычислите интеграл
 ,
где
,
где
 - дуга кривой
- дуга кривой от точки
от точки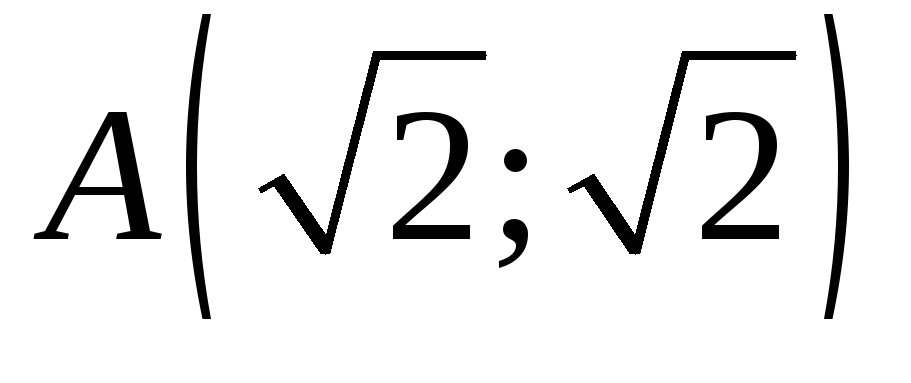 до точки
до точки .
.
1)
![]() ;2)
;2)
 ;3)
;3)
![]() ;4)
2.
;4)
2.
Вычислите интеграл
 ,
где
,
где
 - дуга кривой
- дуга кривой от точки
от точки до точки
до точки .
.
1)
 ;2)
;2)
![]() ;3)
;3)
![]() ;4)
;4)
![]() .
.
Тест №12
Вычислите интеграл
 ,
где
,
где - отрезок прямой
- отрезок прямой от точки
от точки до точки
до точки .
.
1) -2; 2) 2; 3) 3; 4)-6.
Вычислите интеграл
 ,
где
,
где - дуга верхней половины эллипса
- дуга верхней половины эллипса
 от точки
от точки до точки
до точки .
.
1)
![]() ;2)
;2)
![]() ;3)
2; 4)-2.
;3)
2; 4)-2.
Выберите двойной интеграл, к которому с помощью формулы Грина сведется криволинейный интеграл
 .
.
1)
 ;2)
;2)
 ;3)
;3)
 ;4)
;4) .
.
Проверьте справедливость утверждения: криволинейный интеграл
 не зависит от пути интегрирования.
не зависит от пути интегрирования.
1) утверждение справедливо; 2) утверждение несправедливо.
Найдите функцию
 ,
если
,
если .
.
1)
![]() ;2)
;2)
![]() ;
;
3)
![]() ;4)
;4)
![]() .
.
Ответы на тренировочные тесты
|
№ п/п |
№ темы (раздела) |
№ вопроса | ||||
|
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
1.1 |
4 |
3 |
2 |
3 |
2 |
|
2 |
1.2 |
1 |
3 |
1 |
2 |
3 |
|
3 |
2.1 |
3 |
3 |
2 |
2 |
1 |
|
4 |
2.2. |
3 |
3 |
3 |
1 |
1 |
|
5 |
2.3 |
1 |
2 |
3 |
1 |
3 |
|
6 |
3 |
1 |
3 |
2 |
2 |
1 |
|
7 |
4 |
1 |
2 |
3 |
4 |
3 |
|
8 |
5.1 |
2 |
2 |
3 |
1 |
3 |
|
9 |
5.2 |
1 |
3 |
1 |
1 |
1 |
|
10 |
6.1 |
2 |
4 |
4 |
1 |
3 |
|
11 |
6.2 |
3 |
1 |
1 |
4 |
4 |
|
12 |
6.3 |
2 |
2 |
2 |
1 |
3 |
