4. Блок контроля освоения дисциплины

4.1. Методические указания к выполнению контрольных работ

На втором курсе, в третьем семестре студенты выполняют контрольные работы № 5 и № 6.

Прежде чем выполнять контрольные работы, следует изучить теоретический материал по указанной литературе, разобрать решения типовых задач, приведенных в данном комплексе, выработать навыки решения примеров и задач по соответствующей теме, проверив себя по тренировочным тестам, приведенным в 4.3. При выполнении контрольных работ студентам необходимо придерживаться указанных ниже правил:

1. Контрольная работа должна быть выполнена студентом в отдельной ученической тетради в клетку, с полями не менее 3 см для замечаний преподавателя. Студенты, занимающиеся с применением ДОТ, могут выполнить работу письменно (для отправки на проверку письменные работы  необходимо отсканировать)  или в любом текстовом редакторе поддерживающим ввод формул (в формате .doc или .rtf).

2. На титульном листе работы указывается фамилия, имя, отчество студента, шифр (номер студенческого билета), курс, факультет и специальность, по которой студент обучается, номер контрольной работы, год издания методических указаний, из которых взято контрольное задание.

3. Условия задачи переписываются полностью, без сокращения слов, после чего приводится подробное решение со ссылками на использованные при решении определения, теоремы, формулы; в конце решения записывается ответ; чертежи можно выполнять аккуратно от руки.

4. В работу должны быть включены все задачи, указанные в задании, строго по варианту. Контрольные задания, содержащие не все задачи, а также задачи не своего варианта, не зачитываются.

5. Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку.

6. Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления.

4.1.1. Методические указания к выполнению контрольной работы № 5 Дифференциальные уравнения первого порядка

Теоретический материал по теме изложен на с. 20-30 данного издания.

Пример 1. Найти общее решение уравнения

Решение. Разделим обе части уравнения на , полагая, что. Получим

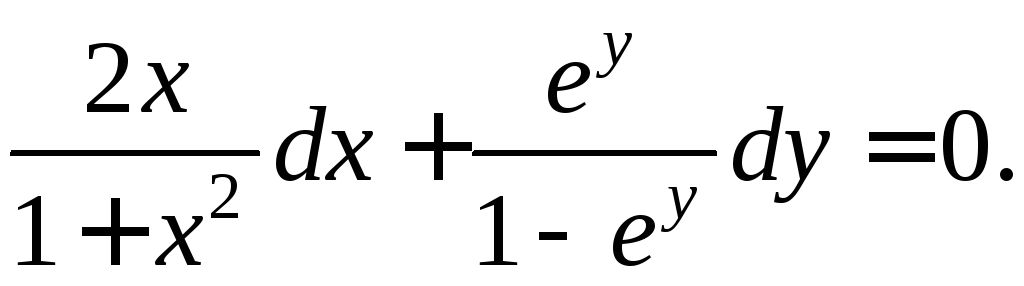
Выполняя интегрирование, будем иметь где- произвольная положительная постоянная, или в таком виде

Если считать, что , то сможем написатьилиСлучайрассматривается аналогично.

Предполагалось, что . Если , тогда . Эта функция является решением уравнения, но получается из общего решения прии не является особым решением.

Пример 2. Найти общее решение уравнения

для и его частное решение, удовлетворяющее начальному условию.

Решение. Переменные в этом уравнении не разделяются. Рассмотрим две функции

Так как обе функции и- однородные первой степени, то уравнение однородное. Чтобы получить уравнение с разделяющимися переменными, сделаем подстановку: где- новая искомая функция. Тогдаили, и исходное уравнение принимает вид:

Упростим его, учитывая, что . ПолучимРазделим переменные и проинтегрируем:

где - произвольная положительная постоянная. Запишем последнее равенство в виде .Подставляя , получаем. Отсюда имеем общее решение:

Найдем теперь частное решение, удовлетворяющее заданному начальному условию. Подставим в выражение общего решения ии найдем значение

Таким образом, частное решение имеет вид: .

Пример 3. Найти общее решение уравнения прии его частное решение, удовлетворяющее начальному условию.

Решение. Это линейное дифференциальное уравнение первого порядка, так как искомая функция и ее производная входят в него в первой степени. Найдем его общее решение, считая, что (случайрассматривается аналогично). Применим метод Лагранжа.

1. Находим общее решение соответствующего однородного уравнения: или. Разделим переменные и проинтегрируем:

где - произвольная положительная постоянная.

2) Общее решение неоднородного уравнения ищем в виде, определяемом общим решением однородного уравнения: , где - новая искомая функция. Найдем и подставимив исходное уравнение:

Отсюда , где- произвольная постоянная. Получаем общее решение:

.

3) Для нахождения частного решения, удовлетворяющего заданному начальному условию, подставляем в выражение общего решения ии находим значение:

Частное решение имеет вид: