prepod / ЛР№18

Лабораторная работа № 18.

Аппроксимация функции, заданной таблично методом наименьших квадратов

Общие сведения

Пусть в результате наблюдений получена таблица совместно наблюдаемых значений:

Таблица 1

x					
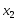
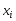
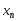
y					

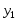
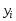
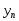
Требуется найти некоторую функцию, заданную аналитически и удовлетворительно описывающую зависимость y от x. Приближенное представление исходной функции с помощью другой функции называется ее аппроксимацией. Выбор вида аппроксимирующей функции остается за исследователем и зависит от ряда соображений. Как правило, предпочтение отдается достаточно простым функциям: линейной, квадратичной, экспоненциальной, логарифмической, обратно пропорциональной. Зачастую выбору конкретной зависимости помогает анализ графика табличной функции, а также физические основания. Выберем класс аппроксимирующих функций, зависящий от нескольких параметров:

(1)

Подставив в формулу (1) эмпирическое значение переменной x= x_i , получим теоретическое значение величины y=y_i^т , вычисленное по формуле

(2)

Разности называются отклонениями и представляют ошибку аппроксимации одного значения данной табличной функции. Для оценки качества аппроксимации функции в целом требуется оценить суммарную ошибку.

Есть разные способы оценки суммарной ошибки аппроксимации, Чаще всего оценивают суммарную квадратичную ошибку, равную сумме квадратов отклонений эмпирических значений функции от теоретических:

(3)

Параметры a₁, a₂, … , a_m должны быть определены из условия минимума суммарной квадратичной ошибки. Запишем необходимое условие экстремума функции многих переменных S(a₁, a₂, … , a_m):

(4)

Формулы (4) представляют собой систему m уравнений с m неизвестными для определения наилучших значений параметров. Если функция (1) линейна относительно параметров a₁, a₂, … , a_m, то система (4) представляет собой систему линейных уравнений.

Метод определения параметров из условия минимума суммарной квадратичной ошибки называется методом наименьших квадратов.

Задаваясь конкретным видом зависимости (1), а именно

1. линейной функцией

y=a₁+a₂x. (5)

2. квадратичной функцией

y=a₁+a₂x+a₃x². (6)

3. экспоненциальной функцией:

. (7)

4. логарифмической функцией

, (8

и т.д., можно получить конкретный вид системы для определения параметров; зная параметры, можно вычислить теоретические значения и построить как график экспериментальной зависимости, так и теоретической.

Достоверность аппроксимации

Квадратичная ошибка (погрешность) аппроксимации функции в соответствии с формулой (3) равна

.

С целью оценки относительной погрешности при аппроксимации функции рассматривают величину суммарной погрешности по отношению к общему разбросу данных. Общий разброс данных складывается из отклонений теоретических значений от среднего и эмпирических значений от теоретических значений. Вводятся обозначения

(9)

(10)

(11)

Величина

(12)

называется коэффициентом детерминированности и характеризует меру точности аппроксимации табличных данных функцией любого вида. Если К² = 1, то ошибка аппроксимации равна 0 и теоретические значения функции совпадают с эмпирическими значениями.

Табличный процессор MS Excel содержит встроенные функции для определения параметров аппроксимации методом наименьших квадратов, а также автоматические средства построения графика аппроксимирующей функции. Графики аппроксимирующих функций в Excel называются линиями тренда.

Задание 1

Построить график зависимости зарплаты от текущего месяца, если рассматривался период относительно устойчивого роста зарплаты в течение четырнадцати месяцев. Данные представлены в таблице 2. Построить графики аппроксимирующих функций (линии тренда)с помощью встроенных средств MS Excel

Таблица 2

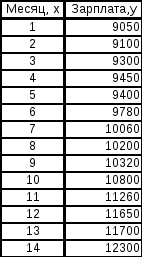
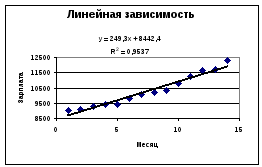Рис.1.

Решение

1. Открыть MS Excel

2. Набрать таблицу данных и оформить ее по образцу

3. Сохранить файл в личной папке

4. Построить график данной функции, заданной таблично с применением Мастера диаграмм. При этом выбрать Тип диаграммы – Точечный, Вид диаграммы – соответствующей отдельным точкам графика

5. Далее построить график линейной аппроксимирующей функции – линию тренда, заданную линейным уравнением. Для этого выполним следующие действия

а) выделим щелчком мыши график функции;

б) вызовем контекстное меню щелчком правой кнопки

в) выполним команду Добавить линию тренда, которая вызовет диалоговое окно этой команды;

г) в диалоговом окне команды Линия тренда зададим Тип аппроксимации - линейная на вкладке Тип;

д) перейдем на вкладку окна Параметра, где установим опции:

показывать на диаграмме уравнение;

поместить на диаграмму величину достоверности аппроксимации R^2;

е) подтвердить выбор нажатием клавиши OK

Результат построения представлен на рис.

6. Построить график квадратичной аппроксимации – квадратичную линию тренда и найти уравнение квадратичной аппроксимации. Для решения этой задачи нужно повторить все действия пунктов 4, 5, но при построении линии тренда выбрать Тип аппроксимации -Полиномиальная степени 2. Если вторая линия тренда строится на той же диаграмме что и первая, то нужно выполнить только п.5

7. Построить график экспоненциальной аппроксимации. Решение очевидно

Результаты решения задачи 1 показаны на рис.1-3.

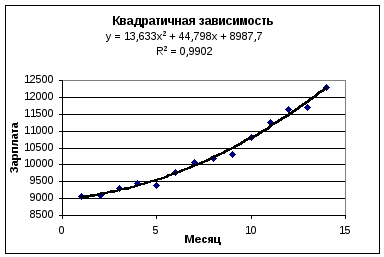
Рис. 2.

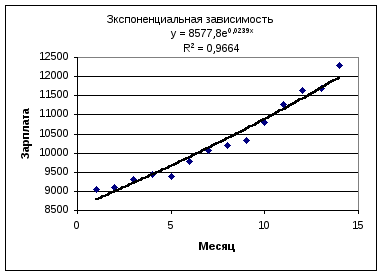
Рис. 3.

Сравним различные способы аппроксимации эмпирических данных различными аналитическими функциями. Наибольшее значение коэффициента детерминированности соответствует квадратичной аппроксимации.

Задание 2

Построить график зависимости загрязнения воздуха сернистым газом от расстояния до источника загрязнения (высокой трубы) и определить, в каком диапазоне расстояний концентрация превосходят предельно допустимую. Предельно допустимая концентрация равна С=0,:6 мг/и³. Наблюдения проводились на различных расстояниях от источника загрязнения период наименьшей интенсивности.

Данные получены в утренние часы при наименьших выбросах промышленного объекта. В дневное и вечернее время загрязненность выше

Решение:

1. Предварительно выполним сортировку данных. Для этого выделим ряды данных по R и C вместе с заголовками и выполним команду Данные|Сортировка. В диалоговом окне укажем Сортировку по возрастанию и по ряду R.

2.

Таблица 2

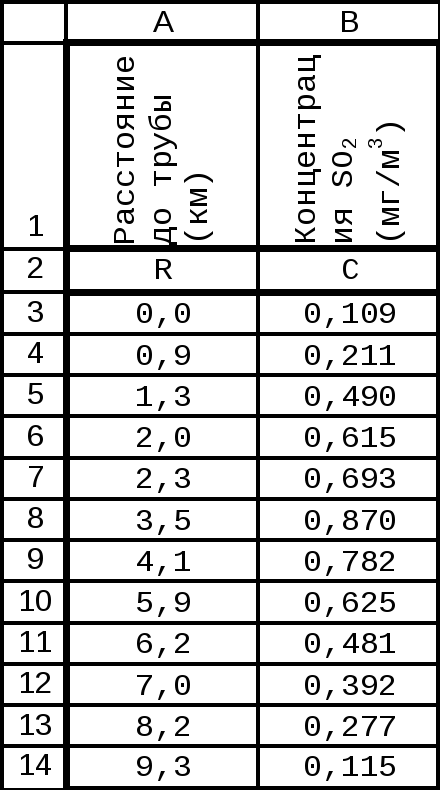
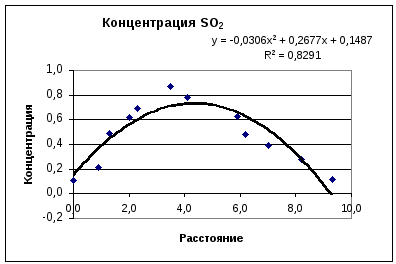Рис. 4.

Сравнение квадратичной линии тренда и графика исходной функции показывает, что выбор уравнения аппроксимации не является удачным. Попробуем использовать полиномиальную аппроксимацию данной функции степени 3. Результат , показанный на рис.5, иллюстрирует улучшение качества аппроксимации, т.к. в большей степени учтена асимметричность исходной функции и сложность ее формы.

Рис. 5.

0