ФИЗИКА3 БОЛЬШЕ ГОТОВОГО1 / 1-st / Механика / alexlab15

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт

имени Г.В. Плеханова (технический университет)

Кафедра общей и технической физики

ЛАБОРАТОРИЯ МЕХАНИКИ

РАБОТА 15

изучение прецессии гироскопа

Выполнил: студент 1 курса, геологоразведочного факультета,

группы РФ-02, Гончаров А.Е.

Проверил: Мезенцев А.П.

САНКТ – ПЕТЕРБУРГ

2003

Цель работы – экспериментально исследовать основные свойства гироскопа, изучить законы вращательного движения твёрдого тела.

Общие сведения

Гироскопом называют массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии. Основное свойство гироскопа - способность сохранять неизменное направление оси вращения при отсутствии действующего на него момента внешних сил. Гироскопы широко применяются в технике: в качестве указателей направления при движении судов, самолетов и т.д.

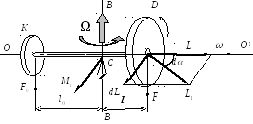Рассмотрим гироскоп, основным элементом которого является диск D, вращающийся со скоростью вокруг горизонтальной оси ОО' (см. рисунок). Ось гироскопа шарнирно закреплена в точке C. Прибор снабжен противовесом К. Если противовес установлен так, что точка C является центром масс системы (m - масса гироскопа; m₀ - масса противовеса К; масса стержня пренебрежимо мала), то без учёта трения запишем:

т.е. результирующий момент сил, действующий на систему, равен нулю. Тогда справедлив закон сохранения момента импульса :

. (1)

Иными словами, в этом случае const; где J - момент инерции гироскопа, - собственная угловая скорость вращения гироскопа.

Поскольку момент инерции диска относительно его оси симметрии есть величина постоянная, то вектор угловой скорости также остается постоянным как по величине, так и по направлению. Вектор направлен по оси вращения в соответствии с правилом правого винта. Таким образом, ось свободного гироскопа сохраняет своё положение в пространстве неизменным.

Если к противовесу К добавить еще один с массой m₁, то центр масс системы сместится и возникнет вращающий момент относительно точки C. Согласно уравнению моментов, . Под действием этого вращающего момента вектор момента импульса получит приращение , совпадающее по направлению с вектором :

                    (2)

Векторы сил тяжести и направлены вертикально вниз. Следовательно, векторы , а по (2), и , лежат в горизонтальной плоскости. Спустя время действующий на систему момент импульса равен

.

Таким образом, вектор изменяет своё направление в пространстве, всё время оставаясь в горизонтальной плоскости. Учитывая, что вектор момента импульса гироскопа направлен вдоль оси вращения, поворот вектора на некоторый угол d за время dt означает поворот оси вращения на тот же угол. В результате ось симметрии гироскопа вращается вокруг неподвижной вертикальной оси ВВ' с угловой скоростью:

.                                      (3)

Такое движение называется регулярной прецессией, а величина - угловой скоростью прецессии.

Выясним зависимость угловой скорости прецессии гироскопа от основных параметров системы. Спроецируем равенство (2) на горизонтальную ось, перпендикулярную ОО'

.

Из геометрических соображений (см. рисунок) при малых углах поворота , а тогда , и угловая скорость прецессии выражается:

.                              (4)

Основные формулы:

• = / t – угловая скорость;

- момент инерции гироскопа;

- максимальная ошибка;

- момент инерции гироскопа с учетом погрешности.

				t	 t					 J
Об/с		Рад.		с.		Рад/с.			кг∙м2
16,7	1,7	141,1	0,005	1. 5,991	0,005	1. 23,602	24,929	0,005	1,295∙10-4	5∙10-8
				2 5,439		2. 25,997
				3. 5,614		3. 25,187
33,3		141,1		1. 8,051		1. 17,563	17,198		0,941∙10-4
				2. 8,193		2. 17,259
				3. 8,431		3. 16,771
50		141,1		1. 15,330		1. 9,224	9,230		1,168∙10-4
				2. 15,189		2. 9,309
				3. 15,440		3. 9,158
66,7		141,1		1. 18,915		1. 7,475	7,359		1,098∙10-4
				2. 19,809		2. 7,138
				3. 18,943		3. 7,464
83,3		141,1		1. 25,491		1. 5,731	5,711		1,133∙10-4
				2. 24,146		2. 5,856
				3. 24,669		3. 5,547

Значение момента инерции гироскопа с учетом погрешностей:

Опыт №1: J=(1.295±0.247)∙10^-4 =(1,127±0,329)∙10^-4

Опыт №2: J=(0.941±0.131)∙10^-4

Опыт №3: J=(1.168±0.11)∙10^-4

Опыт №4: J=(1.098±0.099)∙10^-4

Опыт №5: J=(1.133±0.092)∙10^-4

Вычисления:

Опыт 1.

; ; ;

; ;

.

Вывод: с помощью этого опыта я исследовал основные свойства гироскопа и изучил законы вращательного движения твердого тела.