
- •1. ИНФОРМАЦИЯ О ДИСЦИПЛИНЕ
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •2. РАБОЧИЕ УЧЕБНЫЕ МАТЕРИАЛЫ
- •2.1. Рабочая программа
- •2.2. Тематический план дисциплины
- •2.4. Практический блок
- •2.5. Временной график изучения дисциплины
- •2.6. Балльно - рейтинговая система
- •3. ИНФОРМАЦИОННЫЕ РЕСУРСЫ ДИСЦИПЛИНЫ
- •3.1. Библиографический список
- •Раздел 1. ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- •Раздел 3. ТЕОРИЯ ЛИНЕЙНЫХ И НЕПРЕРЫВНЫХ СИСТЕМ
- •Раздел 4. АНАЛИЗ И СИНТЕЗ ЛИНЕЙНЫХ САУ
- •Раздел 5. ТЕОРИЯ ДИСКРЕТНЫХ САУ
- •Раздел 6. НЕЛИНЕЙНЫЕ СИСТЕМЫ
- •ЗАКЛЮЧЕНИЕ
- •4. БЛОК КОНТРОЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ
- •4.1. Методические указания к выполнению курсовой работы
- •4.2. Методические указания к выполнению контрольной работы
- •4.4. Итоговый контроль. Вопросы к экзаменам и зачету
- •СОДЕРЖАНИЕ
- •Учебно-методический комплекс

Раздел 5. ТЕОРИЯ ДИСКРЕТНЫХ САУ
При работе с данным разделом Вам предстоит:
1) Изучить:
а. Основные понятия о дискретных САУ; б. Математическое представление;
в. Z-преобразование; г. Анализ устойчивости;
д. анализ качества переходных процессов
2)Ответить на вопросы теста № 5.
5.1.Понятия о дискретных САУ
Изучаемые вопросы:
•Представление о дискретных САУ;
•Z-преобразование;
•Преобразование структурных схем
•Анализ качества.
Дискретной системой называется такая САУ, в которой имеет место прерывистый характер передачи информации управления. Такой характер сигналов управления может быть обусловлен включением в систему импульсных или цифровых устройств. В связи с этими все дискретные системы разделяются на две большие группы:
-импульсные САУ;
-цифровые САУ.
Как в импульсных, так и в цифровых системах идет процесс преобразования
непрерывных величин в дискретные (импульсные или цифровые) величины, называемый процессом квантования. Различают три вида квантования: квантование по времени, квантование по уровню, смешанное квантование.
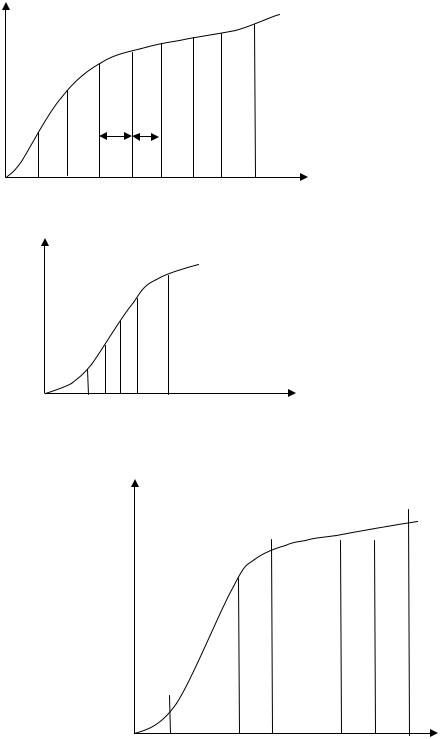
При квантовании по времени осуществляется выборка из множества значений непрерывной величины дискретных значений через равноотстоящие промежутки времени (рис. 5.1). Временной интервал между двумя соседними выборками называется периодом квантования или дискретизации и обозначается через Т.
При квантовании по уровню из множества значений непрерывной величины выбираются значения, совпадающие с одним из уровней квантования (рис. 5.2).
123
f(t)
ТТ
0 1T 2T 3T 4 5 6 7 8T |
t |
|||||||
|
|
|
Рис. 5.1 |
|
||||
f(t) |
|
|||||||
q5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
q4 |
|
|
|
|
|
|||
|
|
|
||||||
q3 |
|
|
|
|
||||
|
|
|||||||
q2 |
|
|
|
|||||
|
|
|||||||
q1 |
|
|
|
|
||||
|
|
|||||||
|
0 |
|
|
|
t |
||
|
|
|
|
|
|||
|
|
Рис. 5.2 |
|||||
При смешанном квантовании выборка осуществляется с постоянным шагом |
|||||||
квантования Т, но в качестве |
f(t) |
|
|
|
|
||
дискретный значений прини- |
q6 |
|
|
|
|
|
|
|
|
|
|
|
|||
маются значения ближайших |
q5 |
|
|
|
|
||
|
|
|
|
||||
уровней квантования (рис. 5.3). |
q4 |
|
|
|
|
||
Смешанное квантование |
|
|
|
|
|||
|
|
|
|
||||
имеет место в цифровых сис- |
q3 |
|
|
|
|
||
темах при преобразовании не- |
q2 |
|
|
|
|
||
прерывных сигналов в цифро- |
|
|
|
|
|||
|
|
|
|
||||
вую форму. |
|
q1 |
|
|
|
|
|
Импульсные |
системы |
|
|
|
|
|
|
разделяются также по типу мо- |
0 |
|
|
|
|
|
|
1T 2T 3T 4 5 6 7 8T t |
|||||||
дуляции в зависимости от того, |
|
|
|
Рис 5 3 |
|||
какой параметр импульса мо- |
|
|
|
||||
делируется непрерывным сигналом. Различают системы с амплитудноимпульсной модуляцией (АИМ), с широтно-импульсной модуляцией (ШИМ), фазоимпульсной модуляцией (ФИМ), частотно-импульсной модуляцией (ЧИМ).
124
В дискретных системах вследствие наличия импульсных или цифровых элементов имеет место прерывистый во времени процесс передачи сигналов управления, поэтому для составления математических моделей приходится пользоваться аппаратом дискретных (решетчатых функций).
Решетчатой функцией времени называется функция дискретного аргумента
– времени. Обозначается она f(nT) или просто f(n), где T –период дискретизации (квантования); n – число периодов с начала отсчета. Для характеристики дискретной функции в интервалах между моментами квантования вводят понятие смещенной решетчатой функции f(nT + σT) или f(n, σ), где σ - относительный сдвиг внутри периода дискретности:
0 ≤ σ < 1.
Аналогом производной непрерывной функции для решетчатых функций является конечная разность:
f(n, σ) = f(n, σ) − f(n−1, σ).
Конечной разностью к-ого порядка называется решетчатая функция kf(n, σ) = k−1f(n, σ) − k−1f(n −1, σ).
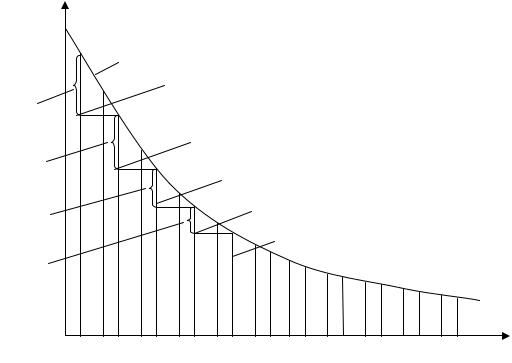
Определение разностей первого порядка для различных n показано на рис. 5.4. f (n,σ)
f (t)
f (0,σ)
f (1,σ)
f (1,σ)
f (2,σ) |
f (2,σ) |
|
f (3,σ)
f (3,σ)
f (4,σ)
f (4,σ)
1T 2T 3T 4T 5T 6 7 |
8 |
9 10 t,n |
Рис. 5.4
Аналогом интеграла непрерывной функции для решетчатой функции является конечная сумма
n−1
f∑ (n,σ) = ∑ f(i, σ).
i= 0
125
Уравнение, связывающее между собой решетчатые функции, их разности различных порядков и конечные суммы, называется разностным уравнением:
a |
0 |
l y(n,σ) + a |
l −1y(n,σ) +... + a y(n,σ) = |
|
1 |
l |
|
= b0 |
k u(n, σ) + b1 |
k −1u(n, σ) + ... + bk u(n, σ) . |
|
Разностные уравнения являются удобной формой представления зависимости между дискретными функциями и широко используются для записи алгоритмов работы цифровых устройств управления.
5.2.Математическое представление дискретных функций
Врассматриваемых системах непрерывная часть имеет значительный вес в сравнении с дискретной и, кроме того, импульсные элементы преобразуют непрерывные сигналы в последовательность импульсов определенной формы. Появляется необходимость учитывать реальную форму импульсов и отразить зависимость того или иного параметра импульсов от мгновенных значений непрерывного сигнала. Использование аппарата решетчатых функций для таких систем оказалось недостаточным. Решетчатая функция дискретного аргумента не может быть непосредственно подвергнута преобразованию Лапласа. Значит, отсутствует возможность составить математические модели, например, в форме передаточных функций или частотных характеристик, широко используемых для моделирования непрерывных частей таких систем. Возникшее противоречие было преодоле-
но за счет применения аппарата δ-функций.
Для того, чтобы описать дискретные сигналы с помощью δ-функций было предложено заменять реальные импульсные элементы (РИЭ) комбинациями из идеальных импульсных элементов (ИИЭ) и формирующих элементов (ФЭ) как показано на рис. 5.3.
Идеальным импульсным элементом называется абстрактный математический элемент, который под воздействием непрерывного сигнала на его входе генерирует мгновенные типа δ-функций импульсы, следующие с интервалом, равным периоду дискретности РИЭ, и по площади равные значения непрерывного сигнала в моменты квантования.
Последовательность δ-функций на выходе ИИЭ
∞
U*f (t) = ∑ f (nT )δ(t −nT ) n=0
126

Формирующим называется элемент, который под воздействием мгновенных модулированных по площади импульсов формирует на выходе импульсы, соответствующие выходному сигналу РИЭ.
Для описания ФЭ привлекается понятие импульсной переходной характеристики. Действительно, каждый импульс на выходе ФЭ есть реакция на входной мгновенный импульс типа δ-функции, т. е. его импульсная переходная характеристика w(t). Подвергнув w(t) преобразованию Лапласа, получают передаточную функцию формирующего элемента
WФЭ(s) = L{w(t)}.
Так, например, для импульса прямоугольной формы, единичной амплитуды и длительностью τ = γT
w(t) =1(t) −1(t − γT ).
Передаточная функция ФЭ W |
(t) = |
1− e−γsT |
. |
|
|
|
|
ФЭ |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При γ = 1 получаем передаточную функцию |
W |
(s) = |
1− e |
−sT |
|||
|
|
так называемого |
|||||
|
|
||||||
|
|
|
ЭО |
s |
|
|
|
|
|
|
|
|
|
|
|
экстраполятора нулевого порядка. В технике такая передаточная функция соответствует преобразователю “код – напряжение”.
Подобным образом получены передаточные функции часто встречающихся на практике импульсных элементов.
Составив математическое описание формирующего элемента, его объединяют с непрерывной частью системы, благодаря чему получается приведенная непрерывная часть (ПНЧ) – рис. 5.5.
f(t) |
|
|
|
f*(t) |
|
|
|
y(t) |
|
|
|
f(t) |
|
|
|
Uf*(t) |
|
|
|
y(t) |
|
РИЭ |
НЧ |
ИИЭ |
ПНЧ |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.5
Преимуществом такого представления участка дискретно-непрерывной системы является то, что выходной сигнал ИИЭ Uf*(t) может быть преобразован по Лапласу, тогда как для сигнала f*(t) на выходе РИЭ преобразование Лапласа недопустимо.
К функции дискретного аргумента f(nT) или f[(n + σ)T] непрерывное преобразование Лапласа не может быть применено, так как функции f(nT) и f[(n + σ)T] не являются однозначными. Для того, чтобы выполнить преобразование Лапласа над функцией дискретного аргумента, последняя должна быть представлена как бесконечная сумма модулированных по площади δ-функций
127
∞
f (t) = ∑ f (nT )δ(t − nT ).
0
Преобразование Лапласа выполненное над суммой модулированных δ- функций, называется дискретным преобразованием Лапласа
∞∞ |
|
|
F*(s) = ∫ |
∑ f (nT )δ(t − nT )e−st dt = |
|
0 0 |
|
|
∞ |
∞ |
∞ |
= ∑ f (nT ) ∫ |
δ(t − nT )e−st dt = ∑ f (nT )e−snT , |
|
0 |
0 |
0 |
∞ |
|
∞ |
так как ∫δ(t − nT )e−st dt = ∫δ(t − nT )e−snT esnT e−st dt = |
||
0 |
|
0 |
∞
= ∫δ(t − nT )e−s(t −nT )e−snT dt = e−snT
0
Для символического обозначения дискретного преобразования Лапласа используется символ
D{f (t)} D{f (nT )} ∞ f (nT )e−snT F*(s) .
= = ∑ =
0
Для записи преобразования над смещенной дискретной функцией f[(n + σ)T] используется символ модифицированного преобразования
D |
{f (t)}= |
∞ |
[(n + σ)T ]e−snT = F*(s,σ) . |
σ |
|
∑ |
|
|
|
0 |
|
Результатом дискретного преобразования функции f(t) является функция трансцендентная, использование которой в преобразованиях затруднительно. Поэтому для описания дискретных систем получило распространение так называемое Z-преобразование, получающееся из дискретного преобразования Лапласа путем формальной замены
|
|
|
|
z = esT , s = |
1 |
ln z . |
|
|
|
|
|
||
|
|
|
|
|
T |
|
Таким образом, F*(s) |
|
|
|
∞ |
|
|
|
s= |
ln z = ∑ f (nT )z−n = F(z) называется Z - преобразованием |
||||
|
|
|
0 |
|
|
|
|
|
T |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
функции f(t). Если в рассмотрение вводится местный локальный сдвиг σ, то вводится понятие модифицированного Z-преобразования.
Zσ{f (t)}= ∑ f [(n + σ)T ]z−n = F(z,σ) .
128

Приведем в качестве примеров непрерывного – и Z-преобразований изображения единичной ступенчатой функции f(t) = 1(t).
|
|
|
|
|
|
∞ |
1 |
|
|
L{f (t)}= L{1(t)}= ∫1(t)e−st dt = |
. |
||||||||
|
|||||||||
|
|
|
|
|
|
0 |
s |
||
|
|
|
|
|
|
|
|
||
Z{1(t)}= Zσ {1(t)}= ∑∞ z−n = |
1 |
= |
|
z |
|
(сумма бесконечной геометрической |
|||
1− z−1 |
z |
−1 |
|||||||
0 |
|
|
|
|
|||||
прогрессии s = 1−a q , где a = 1, q = z-1).
5.3. Z-преобразования
1. Свойство линейности.
Оба преобразования: непрерывное Лапласа и Z-преобразование, - являются линейными, т. е. изображение линейной комбинации функций равно линейной комбинации их изображений.
n |
|
|
|
Так если f (t) = ∑ci fi (t) , то |
|
|
|
i=1 |
|
|
|
L{f (t)}= ∑n |
ci Fi (s), Zσ{f (t)}= ∑n |
ci Fi (z,σ) . |
|
i=1 |
i=1 |
||
• Изображение смещенной функции (теорема сдвига) |
|||
Сдвигу функции оригинала на τ, т. е. |
f1(t) = f (t − τ) соответствует умноже- |
||
ние непрерывного изображения на e−sτ: |
|
|
|
L{f (t − τ)}= e−sτL{f (t)}= e−sτF(s) .
Если сдвиг τ = mT (T - интервал дискретности), то Z – или Zσ - изображения функции f(t) умножаются на Z-m
Zσ{f (t − mT )}= z−mF(z,σ) .
Частотные случаи последнего свойства: 1) m = +1; Zσ{t −T}= z−1F(z,σ) .
Т. е. Z−1 – оператор запаздывания на один период дискретности; 2) m = −1; Zσ{t +T}= zF(z,σ);
Z – оператор опережения на один период дискретности.
• Изображение производной (конечной разности) n -порядка
129
|
n |
|
|
df |
k |
|
|
|
d |
|
|
= sn F(s) , при f(0) = 0 и всех |
|
|
|
||
Если L{f (t)}= F(s), то L |
|
|
f (t) |
|
|
= 0 |
, |
|
|
n |
|
k |
|||||
|
|
|
dt |
|
|
|||
dt |
|
|
|
|
|
|
||
k = 1, 2, …, n-1. Другими словами взятию производной n-го порядка соответствует при нулевых начальных условиях умножение изображения на sn.
Аналогично для Z-преобразования (приводим формулировку свойства для σ = 0) взятию разности k-го порядка дискретной функции f(nT) соответствует умно-
|
|
|
|
z −1 |
k |
z −1 |
k |
|||||||
жение |
ее |
изображения |
на |
|
|
|
|
: |
Z{k f (nT )}= |
|
|
|
F (z) , |
|
z |
z |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
гдеF(z) = Z{f (nT )}.
2. Изображение интеграла (конечной суммы) функции-оригинала Свойства изменения изображений функции после ее интегрирования или
взятия конечной суммы в дискретном варианте является “обратными” по отношению к свойствам дифференцирования или взятия конечных разностей:
L{ |
|
f (t)dt}= 1 F(s), |
где F(s) = L{f (t)}, |
|||||||||
|
∫ |
|
|
s |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
n |
|
|
z |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Z |
∑ f (i) |
= Z |
σ ∑ f (i,σ) |
= |
|
|
F (z,σ) |
|||||
z −1 |
||||||||||||
|
|
=0 |
|
|
|
|
|
|
||||
i |
|
|
i=0 |
|
|
|
|
|
||||
Резюмируя свойства 3 и 4 отметим, что s – оператор дифференцирования в непре-
рывной области; 1/s – оператор интегрирования в непрерывной области; |
z |
|
- |
|||
z− |
1 |
|||||
оператор суммирования в дискретном времени; |
z− |
1 |
- оператор взятия конечной |
|||
z |
|
|||||
разности 1-го порядка.
• Свойство изображения свертываемых функций (теорема свертки) Сверткой двух непрерывных или дискретных функций называется функция,
t
значения которой вычисляются согласно f (t) = ∫ f1(τ) f2(t − τ)dτ для непрерывно-
0
n
го времени и f (n,σ) = ∑ f1(i,σ) f2(n − i,σ) для дискретного времени. i=0
Формулировка свойства об изображении свертки одинакова для непрерывного и дискретного времени:
- изображение свертки равно произведению изображений свертываемых функций.
Если L{f1(t)}= F1(s) и L{f2(t)}= F2(s) , то
130

t
L ∫ f1(τ)
0
Если Zσ{f1(n,σ)}= F1(z,σ) и Zσ{
∑n
Zσ f1(i,σ)
i=0
f2(t − τ)dτ = F1(s)F2(s) .
f2(n,σ)}= F2(z,σ) , то
f2(n − i,σ) = F1(z,σ)F2(z,σ) .
3.Определение начального значения функции оригинала по известному изображению
Зная изображение (F(s) в непрерывном случае и F(z) или F(z,σ) в дискретном случае) можно сравнительно просто вычислить начальное и конечное значения функции-оригинала.
Начальное значение непрерывной функции |
|||||||
f (t) = limsF(s) . |
|||||||
t →0 |
|
s→∞ |
|
|
|||
Начальное значение дискретной функции |
|
|
|
|
|
|
|
f (nT ) = lim |
z −1 |
F(z) . |
|||||
|
|
||||||
n=0 |
z→∞ |
z |
|
|
|||
4. Конечное значение функции-оригинала |
|||||||
В непрерывном времени f (t) = limsF(s) . |
|
|
|||||
t →∞ |
s→0 |
|
|
||||
В дискретном времени f (nT ) = lim |
z −1 |
F(z) и при σ ≠ 0 |
|||||
|
|||||||
n→∞ z→1 |
|
z |
|
|
|||
lim f [nT + σT ] = |
|
lim |
z −1 |
F(z,σ) . |
|||
z |
|
||||||
n→∞ |
|
→1 |
z |
||||
0≤σ<1 |
|
0≤σ<1 |
|
|
|||
Рассмотрим еще несколько свойств, полезных для выполнения несложных преобразований.
5. Свойство изображения функции, умноженной на e±αt
Для дискретного времени это свойство записывается следующим образом:
Если F(z,σ) = Zσ{f (t)}, то Zσ{f (t)e±αt }= d σF(dz ,σ), где d = e±αT .
В частном случае σ = 0 имеем
Z{f (t)e±αt }= F(dz ) , где d = e±αT .
Записанное свойство позволяет без труда найти изображение экспоненциальной функции
131

Z{e |
±αt |
}= Z{1e |
±αt |
}= Z{1(t)} |
|
z= ±αT |
= |
z |
z= z |
= |
z |
; |
||||
|
||||||||||||||||
|
|
|
z −1 |
|
z − e±αT |
|||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e±αt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z
z − e±αT .
Для непрерывного времени в рамках этого свойства определяется изображение f (t) = e±αt
L{e±αt }= s 1 α.
6. Свойство изображения функции, умноженной на tm (m – целое число) Это свойство имеет особое значение для дискретных систем, так как для не-
прерывных систем составлены подробнейшие таблицы соответствий функций и их изображений [6].
Для дискретных систем свойство формулируется отдельно для случаев σ = 0
и σ ≠ 0.
Для σ = 0 имеем
Z{f (t)t m }= (−Tz)m d m F (z). dZ m
Словами: умножению функции-оригинала tm соответствует, с точностью до множителя, взятие m-производной в области изображений.
Пример. f (t) =1(t), m =1.
Z{1(t)t}= Z{t}= −Tz |
d |
|
z |
|
= −Tz |
z −1− z |
= |
Tz |
. |
|
|
|
|
|
|
|
|
||||
|
|
|
(z −1)2 |
(z −1)2 |
||||||
|
dz z −1 |
|
|
|
|
|||||
Для σ ≠ 0 выражение изображения находится более сложно:
Zσ{f (t)t m }= ∑m (−1)i (σT )m−i Cmi d i F(z,σ) |
|
||
|
. |
||
i=0 |
dsi |
|
z=esT |
|
|
||
Здесь Cmi - число сочетаний из m элементов по i.
5.3.1. Связь спектров непрерывного и дискретного сигналов
Для выяснения соотношения между Z-преобразованием и непрерывным преобразованием Лапласа, а также соотношения частотных свойств дискретного и непрерывного сигналов рассмотрим связь спектров этих сигналов.
132

Спектр непрерывного сигнала x(t) определяется его преобразованием Фурье
∞
X ( jω) = ∫x(t)e− jωt dt , где ω = 2πf – круговая частота сигнала, −∞ ≤ ω ≤ ∞.
0
Чтобы найти выражение спектра дискретного сигнала, его надо предварительно представить в непрерывной форме с помощью δ-функций
∞
x*(t) = ∑x(nT )δ(t − nT ) = x(t)U *(t) ,
−∞
где U*(t) – последовательность δ-функций, следующая с периодом T. Как периодическую функцию U*(t) можно разложить в ряд Фурье
∞ |
∞ |
U *(t) = ∑δ(t − nT ) = ∑Uk e jkω0t , |
|
−∞ |
−∞ |
где ω0 = 2Tπ - круговая частота квантования, Uk – коэффициент ряда Фурье:
|
|
|
|
|
T |
|
|
T |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
2 ∞ |
− jkω0t dt = |
1 |
2 |
|
|
1 |
|
||||||
U |
|
= |
|
|
|
|
∑δ(t − nT )e |
|
|
|
δ(0)dt = |
; |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
k |
|
T |
|
∫T −∞ |
|
T |
|
∫T |
T |
|
|||||||
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
следовательно все коэффициенты ряда Фурье равны независимо от значения k. Для всей суммы δ-функций
∞ |
1 |
|
U *(t) = ∑Uk e jkω0t = |
||
T |
||
−∞ |
Подставляя U*(t) в выражение сигнала, получим
∞
∑e jkω0t .
−∞
x*(t) = x(t) 1 ∑∞ e jkω0t .
T −∞
В таком виде сигнал x*(t) может быть подвергнут преобразованию Фурье:
∞ |
1 |
∞ |
1 |
∞ ∞ |
1 |
∞ |
|
X *( jω) = ∫x(t) |
∑e jkω0te jωt dt = |
∑ ∫x(t)e j(ω−kω0 )t dt = |
∑X[ j(ω− kω0)] |
||||
T |
T |
T |
|||||
0 |
−∞ |
−∞0 |
−∞ |
где X[ j(ω− kω0)] - смещенный на kω0 спектр непрерывного сигнала.
Общий вывод: спектр дискретного сигнала представляет бесконечную сумму (рис. 5.6) смещенных спектров непрерывного сигнала.
133
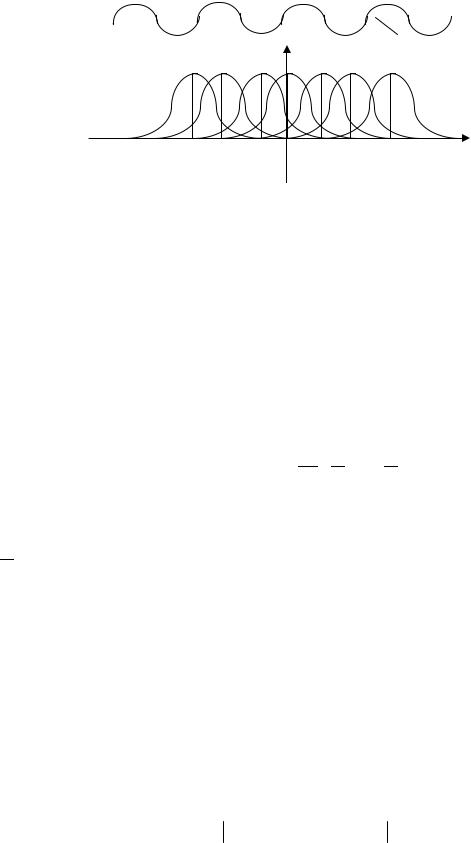
(1/T)/X(jω)/ /X*(jω)/
-3ω0 -2ω0 -ω0 0 ω0 2ω0 3ω0 |
ω |
Рис. 5.6
Это значит, что при определенной частоте квантования частотные характеристики дискретных систем будут представлять сумму смещенных частотных характеристик соответствующих непрерывных систем. Это также означает, что если максимальная частота спектра непрерывного сигнала (ωм) или, максимальная частота пропускания непрерывной части системы (ωп) меньше половины частоты квантования ω0, то наложение отдельных составляющих спектра не будет, и характеристики дискретной системы в существенном диапазоне частот будут совпадать с характеристиками непрерывной системы.
И так для системы необходимо ωп≤ ω20 = Tπ ,ωп≤ Tπ .
Для неискаженной передачи непрерывного сигнала его дискретными значениями необходимо, чтобы максимальная частота спектра непрерывного сигнала
ωм≤ Tπ .
Последнее условие является стержнем знаменитой импульсной теоремы Котель- никова-Шеннона, согласно которой частота квантования ω0 =2π/T должна быть по крайней мере в 2 раза больше максимальной частоты спектра непрерывного сигнала, передаваемого его дискретными значениями.
5.3.2.Связь между непрерывным преобразованием Лапласа
иZ-преобразованием
Из выражений непрерывных преобразований Лапласа и Фурье, приводимых ранее, следует, что F( jω) = F (s) s= jω и F(s) = F( jω) jω=s . Используем эти соотношения для преобразований дискретных сигналов и получим
134
|
|
|
|
1 |
∞ |
|
|
|
|
|
F*(s) = F*( jω) |
|
= |
∑F(s − jkω0) . Если ввести замену esT = z , получим |
|||||||
jω=s |
T |
|||||||||
|
|
−∞ |
|
|
|
|
||||
|
|
|
|
|
|
|||||
связь непрерывного преобразования Лапласа и Z-преобразования |
||||||||||
|
|
|
|
|
|
1 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
F(z) = |
|
∑ f (s − jkω0) |
|
. |
|
|
|
|
|
|
T |
|||||
|
|
|
|
|
|
-∞ |
|
esT =z |
||
|
|
|
|
|
|
|
|
|||
Символически эту связь записывают следующим образом:
|
1 |
∞ |
|
|
|
|
F(z) = Z{F(s)}при σ = 0 и F(z,σ) = |
Tσ(s− jkω0 ) |
|
|
|
||
T |
∑F(s − jkω0)e |
|
|
, |
||
|
−∞ |
|
s= |
ln z |
|
|
|
|
|
T |
|||
|
|
|
|
|||
что символически означает F(z,σ) = Zσ{F(s)}.
Записанные выражения связи F(z), F(z,σ), F(s) имеют главным образом, теоретическое значение и не используются для практического определения F(z) и F(z,σ) по F(s). Существует два способа практического перехода от F(s) к F(z) и F(z,σ).
1 способ.
Предварительно определяется временная функция, соответствующая исходному изображению f (t) = L−1{F(s)}.
Чтобы облегчить переход в дискретную область, можно предварительно разложить F(s) на сумму простых слагаемых.
Пример. Пусть |
F(s) = |
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
s2(s +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Разложение на простые слагаемые дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
= |
1 |
− |
1 |
+ |
|
1 |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
s |
+1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
s2(s +1) s2 |
|
|
|
|
|
|
= L{e−t }. Таким обра- |
||||||||||||||
Из таблиц соответствия имеем: |
|
1 |
|
= L{t}; |
−1 = L{−1}; |
1 |
|
||||||||||||||||||||||
|
s2 |
s +1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
||||||
−1 |
|
|
1 |
|
|
|
|
−t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
зом f (t) = L |
|
|
|
|
|
= t −1 |
+ e |
|
|
. Подвергая f(t) Z-преобразованию, получим: |
|||||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
s |
|
(s +1) |
|
|
|
|
|
|
|
|
}= |
|
|
|
|
|
|
|
|
|
|
|
||||||
Z{f (t)}= Z{t}− Z{1(t)}+ Z{e−t |
Tz |
|
− |
|
z |
|
+ |
z |
. |
||||||||||||||||||||
(z −1)2 |
|
z −1 |
z − e−t |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 способ.
Осуществляется непосредственный переход от F(s) к F(z), используя таблицу соответствия изображений [6]. Если в таблице нет изображения, соответствующего заданному F(s), выполняют разложение F(s) на сумму более простых выражений.
135

Пример. Пусть F(s) = |
|
|
|
|
|
k |
|
|
|
. Представим заданное F(s) суммой сла- |
|||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 П (T s +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
=3 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k1 |
|
|
|
k2 |
|
|
|
|
5 |
|
|
ki |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
гаемых |
F(s) = |
+ |
|
+ ∑ |
|
|
|
|
, где si = − |
|
. Определим модифицированное Z- |
||||||||||||||||||||||||||
|
|
s |
|
|
|
s2 |
|
|
|
|
i=3s − si |
|
|
|
|
|
|
Ti |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
преобразование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
k |
|
|
5 |
|
k |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
i |
|
|
||||||||||||||||||
|
Zσ |
|
|
|
|
|
|
|
|
|
|
Zσ |
1 |
+ Z |
σ |
|
|
|
+ ∑Zσ |
|
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
|
s2 П (T s |
+1) |
s |
|
|
|
|
s |
|
i=3 |
s − si |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
i |
=3 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
σTz |
|
|
|
|
|
|
Tz |
|
|
|
5 |
|
|
|
z |
|
|
|
||||||
|
= k1 |
|
|
|
|
|
+ k2 |
|
|
+ k2 |
|
|
|
|
+ ∑kie−siTσ |
|
|
|
. |
||||||||||||||||||
|
|
z −1 |
z −1 |
|
(z −1)2 |
|
z − e−siT |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=3 |
|
|
|
||||||||||||||||||||
Частный случай, важный в практике записи Z-изображений по заданному
F(s).
Если |
F(s) = F |
(esT )F |
(s) , то Z |
σ |
{F(s)}= F (esT ) |
|
|
|
|
|
F (z, |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
esT =z |
2 |
|
|
|||||
|
Пример. Пусть F(s) = k(1− e−sT ) |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||
|
s(T s +1) |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
Zσ{F(s)}= k(1− z−1)Zσ |
|
|
|
|
|
. |
|||||||||||||||||||
|
|
|
|
s(T s |
+1) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tσ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
z |
|
− T1 |
||||||
|
Z |
σ |
|
|
|
= Zσ |
|
− |
|
|
|
|
|
= |
|
|
|
|
|
|
− e |
|
|
||||||
|
|
|
|
|
|
1T |
|
|
z −1 |
|
|
||||||||||||||||||
|
|
s(T1s |
+1) |
|
|
|
s |
|
s + |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
Tσ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
F(z,σ) = k(1− z−1 |
|
z |
|
|
|
− e |
T1 |
|
|
|
|
|
|
= k(1 |
− e |
|||||||||||||
|
|
|
|
|
|
|
|
T |
|
|
|||||||||||||||||||
|
|
|
|
|
|
z −1 |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z − e |
T1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
σ).
|
|
|
z |
|
|
|
. |
|
|
|
|
|
|
|
− |
T |
|
|
|
||
|
z − e |
T1 |
|
|
|
|
||||
|
|
|
|
|
|
|||||
Tσ |
|
z −1 |
|
|
||||||
T1 |
|
|
). |
|||||||
|
|
|
|
|
− |
|
T |
|
||
|
|
|
|
|
T1 |
|
|
|||
|
|
|
z − e |
|
|
|||||
5.3.3. Обратное преобразование Лапласа
Обратным преобразованием Лапласа L−1{F(s)}называется определение временной функции f(t), для которой прямое преобразование Лапласа
136
L{f (t)}= ∞∫ f (t)e−st dt = F(s) .
0
Обратным Z-преобразованием Z −1{F(z)} или Zσ−1{F(z,σ)} называется оп-
ределение дискретной функции времени f(nT) (f[(n + σ)T]), для которой
Z{f (nT )}= F(z)или Zσ{f [(n + σ)T ]}= F(z,σ) .
Отметим ограничения, которые следует иметь в виду, выполняя обратное преобразование Лапласа или обратное Z-преобразование.
1.Не каждая функция F(s) имеет обратное преобразование. Существование обратного преобразования определяется необходимыми и достаточными условиями, накладываемыми на F(s).
2.Прямое преобразование Лапласа L{f (t)} единственно для каждой f(t),
имеющей такое преобразование. Обратное утверждение, в общем случае, несправедливо. Различные разрывные функции могут иметь одинаковое преобразование Лапласа. Например, единичная ступенчатая функция f(t) = = 0 для t < 0 и f(t) = 1 для t > 0 имеет преобразование Лапласа 1/s независимо от значения, принимаемого при t = 0.
3. Обратное Z – или Zσ - преобразование, если оно существует, позволяет определить лишь последовательность отдельных значений непрерывной функ- ции-оригинала, существующих в моменты времени t = nT или t = (n + σ)T. Одной и той же последовательности дискретных значений f(тT) или f[(n + σ)T] может соответствовать множество огибающих f(t). Поэтому по обратному Z – преобразованию принципиально невозможно восстановить непрерывную функцию f(t).
Существует два общих практических способа определения обратных преобразований как для непрерывных, так и для дискретных систем.
1.Использование таблиц обратных преобразований Лапласа и обратных Z– преобразований, например в [6]. Если исходного F(s) и F(z) изображения нет в таблице следует использовать разложение его на сумму или произведение изображений, имеющихся в таблице.
2.Использование формулы обращения.
Для непрерывного изображения
|
σ + j∞ |
||
f (t) = |
1 |
1 |
∫ F(s)est ds . |
2πj |
|
||
|
|
− j∞ |
|
|
σ1 |
||
137

Значение контурного интеграла определяется в открытом интервале, где f(t) ограничена и имеет конечное число точек экстремума и разрыва. Решение часто удается получить при помощи теоремы о вычетах:
1 |
|
n |
|
|
|
|
F(s)est ds = ∑ResF(z |
|
), |
||
2πj c∫ |
k |
||||
k =1 |
|
||||
где z1, z2, …, zn особые точки F(s)est .
Вычисление интеграла обращения как суммы вычетов широко используется в различных программных продуктах, используемых при компьютерном моделировании систем автоматического управления.
Для дискретного изображения формула обращения имеет вид
f (n,σ) = 1 ∫F(z,σ)zn−1dz . 2πj R
Контур интегрирования R должен охватывать начало координат плоскости Z и все особые точки подынтегральной функции. Как и в непрерывном случае, круговой интеграл обычно рассчитывается как сумма вычетов подынтегральной функции в особых точках:
f (n,σ) N Resi[F(z,σ)zn−1].
= ∑
i=1
N – число вычетов; N = q + 1 для n = q для n > 0, где q – число особых точек
функции F(z,σ). |
|
|
|
|
|
|
|
Вычеты вычисляются следующим образом: |
|
|
|
||||
- для простого полюса z = zi |
|
|
|
|
|
||
Res [F(z,σ)zn−1] = |
lim [F(z,σ)zn−1(z −z |
)]; |
|
||||
i |
|
|
z→zi |
|
i |
|
|
z=zi |
|
|
|
|
|
|
|
- для кратного полюса кратности m |
|
|
|
|
|||
Res [F(z,σ)zn−1] = |
1 |
|
lim |
d m−1 |
[F(z,σ)zn−1(z −z |
)m ]. |
|
|
|
|
|||||
i |
(m −1)!z→zi |
dzm−1 |
|
i |
|
||
z =zi |
|
|
|
||||
Кроме двух общих методов, в случае обратного Z–преобразования используется также разложение F(z,σ) в ряд по возрастающим степеням z-1 в соответствии с основной формулой Z–преобразования
F(z,σ) ∞ f (n,σ)z−n .
= ∑
n=0
138

Когда F(z,σ) представлено рациональной дробью разложение по степеням z-1 может быть выполнено простым делением числителя на знаменатель.
Пример. Пусть F(z) = |
z |
. |
|
||
|
|||||
|
|
|
z − 0.2 |
||
z |
|
z-0.2 |
|
|
|
|
|
|
|
||
z-0.2 |
|
1+0.2z-1 + 0.04z-2 + 0.008z-3 + … |
|
||
0.2 |
|
|
|
|
|
0.2– 0.04z-1 0.04z-1
0.04z-1 – 0.008z-2 0.008z-2
Получаем f(n) = 1 0.2 0.04 0.008.
При более сложных выражениях F(z) и F(z,σ) лучше использовать вычисление по рекуррентной формуле:
|
b0 |
|
1 |
k |
|
f (q − p,σ) = |
; f (k + q − p,σ) = |
[bk − ∑ai f (k − i + q − p,σ)]. |
|||
|
a0 |
||||
|
a0 |
i=1 |
|||
Здесь b0, …, bk, …, bp – коэффициенты числителя F(z,σ) a0, …, ai, …, aq – коэффициенты знаменателя F(z,σ). При q = p формулы значительно упрощаются
|
b0 |
|
|
1 |
k |
|
f (0,σ) = |
; |
f (k,σ) = |
[bk − ∑ai f (k − i,σ)] |
|||
|
a0 |
|||||
|
a0 |
|
i=1 |
|||
Аналогично преобразованию дифференциального уравнения непрерывной системы осуществляется Z-преобразование разностного уравнения дискретной системы.
Пусть дискретная система описывается уравнением
a0 n y(n,σ) = b0 m g(n)
+ a |
n−1y(n,σ) +... + a |
n |
y(n,σ) |
= |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
+ b |
m−1g(n) +... + b g(n) + c |
0 |
e f (n) + c |
e−1 f (n) +... + c |
e |
f (n), |
||
1 |
m |
|
|
1 |
|
|
||
Подвергнем это разностное уравнение Z-преобразованию, принимая начальные условия нулевыми:
a0(z z−1)nY (z,σ) + a0( zz−1)n−1Y (z,σ) +... + anY (z,σ) =
=b0( zz−1)m G(z) + b1( zz−1)m−1G(z) +... + bmG(z) +
+c0(zz−1)e F(z) + c1( z−z 1)e−1F(z) +... + ceF(z).
Записывая полученное уравнение в сжатой форме, получим
A(z,σ)Y (z,σ) = B(z)G(z) +C(z)F(z).
139

Беря отношения Z-изображений, получим передаточные функции дискретной системы по управляющему и возмущающему воздействиям:
Wg (z,σ) = |
B(z) |
= |
Y (z,σ) |
; W f (z,σ) = |
C(z) |
= |
Y (z,σ) |
. |
A(z,σ) |
G(z) |
A(z,σ) |
|
|||||
|
|
|
|
F (z) |
||||
Для дискретно-непрерывной системы определение дискретной передаточной функции выполняется на основе перехода от непрерывной передаточной функции приведенной непрерывной части к ее дискретному эквиваленту в Z- области. Покажем этот переход на примере разомкнутой дискретно-непрерывной системы с одним импульсным элементом на ее входе (рис. 5.7). На схеме
∞
U *g (t) = ∑g(nT )δ(t − nT ), WПНЧ(s) =WФЭ(s)WНЧ(s).
0
|
|
|
|
|
|
|
Ug*(t) |
|
g(t) |
|
|
|
|
|
WПНЧ(s) |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.7
ПНЧ на δ-функции; т.
Так как входной сигнал приведенной непрерывной части представляет собой сумму модулированных по площади входным сигналом g(t) δ-функций, выходной сигнал y(t) будет представлять сумму реакции
е. сумму функций веса ПНЧ
t
y(t) = ∑g(iT )wПНЧ(t − iT ).
0
Если вместо непрерывного сигнала y(t) отмечать лишь его дискретные значения y(nT) или y[(n + σ)T], то получим решетчатую функцию y(n) или y(n, σ):
n
y(n,σ) = ∑g(i)wПНЧ(n − i,σ).
i=0
Подвергнем эту решетчатую функцию модифицированному Z- преобразованию
n |
|
|
|
|
|
Zσ{y(n,σ)}= Zσ |
∑g(i)wПНЧ(n − i,σ) . |
|
|
|
|
i=0 |
|
|
С учетом теоремы свертки имеем
Y (z,σ) = G(z)Zσ{wПНЧ(n,σ)},
Zσ{wПНЧ(n,σ)}= Zσ{L−1{WПНЧ(n,σ)}}= Zσ{WПНЧ(n,σ)}=W (z,σ).
Таким образом
Y (z,σ) = G(z)W(z,σ).
Здесь W (z,σ) = Y (z,σ) - дискретная передаточная функция разомкнутой дискрет-
G(z)
но-непрерывной системы. С одной стороны, она связывает Z-изображения дис-
140
кретных сигналов, с другой стороны, она определяется как Z-форма передаточной функции приведенной непрерывной части.
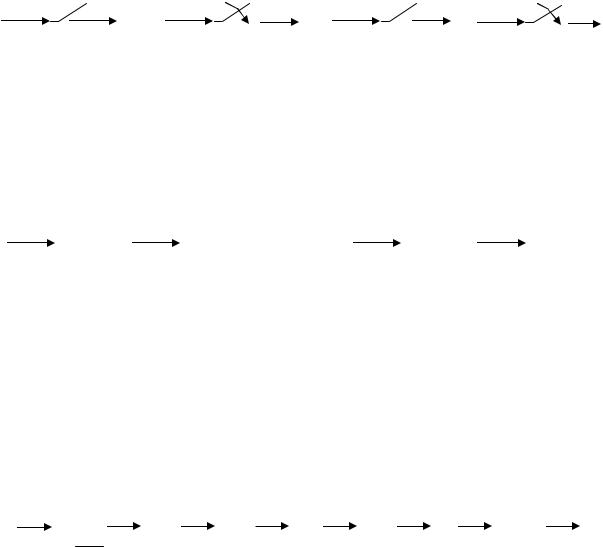
5.4.Структурные схемы
Вструктурных схемах дискретных систем импульсные (дискретные) элементы изображаются ключами (рис. 5.8.). Иногда ключ снабжается замыкающей стрелкой и большой буквой T, которая означает, что элемент осуществляет квантования с периодом T.
≡ |
T |
T |
≡ |
≡ |
|
|
Рис. 5.8 |
|
Идеальный импульсный элемент изображается прямоугольником с символом δ- функции внутри (рис. 5.9, а).
Формирующий элемент изображается как обычное непрерывное звено прямоугольником с записью его передаточной функции (рис. 5.9, б).
x (t) |
|
|
|
|
u*x(t) |
u*x(t) |
WФЭ |
x*(t) |
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
а) |
Рис. 5.9 |
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Кроме общих структурных схем широко используются детализированные структурные схемы, состоящие только из безинерционных масштабных звеньев и идеальных интегрирующих звеньев с полностью вскрытыми связями между ними.
5.4.1. Дискретно-непрерывная система
x |
|
|
|
|
W1 |
|
W2 |
|
|
|
Wn |
y |
|
x |
W(z) |
y |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W(z) = Z{W1(s)W2(s)…Wn(s)} = W1W2W3…Wn(z)
141

Правило: Дискретная передаточная функция последовательного соединения непрерывных звеньев не равна произведению их Z-форм, а равна Z-форме произведения их непрерывных передаточных функций.
5.4.2. Дискретная система с несколькими импульсными элементами
x |
|
|
|
|
W1 |
|
|
|
|
|
W2 |
y |
|
x (z) |
W(Z) |
y |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W(z) = W1(z)W2(z), где W1(z) = Z{W1(s)}, W2(z) = Z{W2(s)}.
Правило: Передаточная функция нескольких последовательно соединенных непрерывных звеньев, разделенных импульсными элементами, равна произведению их Z-форм от непрерывных передаточных функций.
Дискретно-непрерывная система
n
W(z) = ∑Wi (z) , где Wi(z) = Z{Wi(s)}
i=1
Правило: Дискретная передаточная функция параллельного соединения непрерывных звеньев равна сумме дискретных передаточных функций отдельных ветвей.
|
W1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x(z) |
|
W1* |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(z) |
|
|
y(z) |
||||||
|
|
|
|
y |
|
y(z) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
W2 |
|
|
|
|
|
|
|
|
|
|
W2* |
|
|
|
|
|
|
|
|
|
|
W(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W3 |
|
|
|
|
|
|
|
|
|
|
Wn* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретная система с несколькими импульсными элементами
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
|
|
|
|
|
x1 |
|
k1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
kn |
|
|
|
|
|
|
|
|
xn |
|
|
|
kn |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
142

Правило: Параллельные каналы с безинерционными звеньями и импульсными элементами, работающими синхронно и с одинаковым периодом квантования, могут быть заменены одним импульсным элементом, включенным после узла суммирования.
Дискретно-непрерывная система с единичной обратной связью
X(s) E(s) |
|
|
|
|
|
|
Y( |
|
s) |
||||
|
|
|
|
|
Wпнч(s) |
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y(z,σ ) = W(z,σ )E(z), где W(z,σ ) = Zσ{WПНЧ(s)}, E(z) = X(z) – Y(z). Подставляя в уравнение выхода, получаем
Y(z,σ ) = W(z,σ )X(z) - W(z,σ )Y(z).
Положим σ =0, тогда |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Y(z) = W(z)X(z) - W(z)Y(z) = |
|
|
|
W (z) |
|
X (z) . |
|
|
||||
|
1 |
+W (z) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
Подставляя в уравнение для Y(z,σ ), получим |
|
|
|
|
|
|
|
|
|
|
||||
|
Y(z,σ ) = W(z,σ )[X(z) - Y(z)] = W(z,σ )[X(z) - |
|
|
W (z) |
X(z)] = |
W (z,σ) |
X(z). |
|||||||
1+W (z) |
1+W (z) |
|||||||||||||
|
|
|
|
|
|
|
||||||||
Передаточная функция замкнутой системы по управлению: |
|
|
||||||||||||
|
|
Фx(z,σ ) = Y (z,σ) = |
W (z,σ) |
. |
|
|
|
|||||||
|
|
|
|
|
||||||||||
|
|
X (z) |
1+W (z) |
|
|
|
||||||||
Получим передаточную функцию замкнутой системы по ошибке: |
|
|||||||||||||
|
|
Фе(z,σ )= E(z,σ) |
, |
|
|
|
|
|
|
|||||
|
|
|
X (z) |
|
|
|
|
|
|
|
|
|
||
где E(z,σ ) = X(z,σ ) - Y(z,σ ). Подставляя в |
|
уравнение для |
ошибки |
Y(z,σ ) = |
||||||||||
= |
W (z,σ) |
X(z), получим E(z,σ ) = X(z,σ ) - |
W (z,σ) |
X(z). |
|
|
|
|||||||
|
|
|
|
|
||||||||||
1+W (z) |
1+W (z) |
|
|
|
||||||||||
К сожалению, из полученного выражения E(z,σ ) невозможно написать отношение E(z,σ ) к X(z). Это можно сделать, только положив σ=0, тогда
E(z) = X(z) - |
W (z,σ) |
X(z) = |
1 |
|
X(z). Тогда передаточная функция замкнутой |
|||||
1+W (z) |
1+W (z) |
|||||||||
|
|
|
|
|
|
|
||||
системы по ошибке при σ=0 будет: |
|
|
|
|
|
|||||
|
|
|
Фе(z) = |
|
E(z) |
= |
|
1 |
. |
|
|
|
|
|
X (z) |
1+W (z) |
|||||
|
|
|
|
|
|
|
||||
143

Отметим, что по форме передаточные функции замкнутой дискретнонепрерывной системы полностью совпадают с соответствующими передаточными функциями непрерывной системы.
Дискретные системы произвольной структуры
Под произвольной структурой мы будем понимать расположение одного или нескольких импульсных элементов в различных местах дискретной системы, (в прямом канале, в канале обратной связи, между непрерывными звеньями и т.д.). Для записи уравнений или передаточных функций в таких системах следует использовать три основных правила записи уравнений в Z-изображениях.
*Правило1: Z-изображение выходного сигнала одного или нескольких последовательно соединенных непрерывных звеньев, подвергнутых воздействию дискретного сигнала, равно произведению Z-изображения, входного сигнала на Z- преобразование непрерывной передаточной функции. Рисунок ниже иллюстрирует это правило:
|
|
|
|
|
X(z) |
|
|
|
Y(z)=X(z)W1W2(z) |
X(z) |
|
|
|
|
|||||
|
W(s) |
|
Y(z)=X(z)W(z) |
W1(s) |
|
W2(s) |
|||
|
|
|
|
|
|
|
|||
|
|
Y(z,σ)=X(z)W(z,σ), |
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
Y(z,σ)=X(z)W1W2(z,σ), |
|||||
|
|
|
|
||||||
|
|
|
где W(z)=Z{W(s)} |
|
где W1W2(z)=Z{W1(s)W2(s)}, |
||||
W1W2(z,σ)=Z σ{W1(s)W2(s)}.
Правило2: Если одно или группа непрерывных последовательно соединенных звеньев подвергнута воздействию непрерывного сигнала, то Z-изображение выходного сигнала равно Z-преобразованию произведению изображения входного сигнала на непрерывные передаточные функции звеньев.
|
|
|
|
|
|
|
|
X(s) |
W(s) |
Y(s) |
X(s) |
W1(s) |
|
W2(s)Y(s) |
|
|
|
|
|
|
|
|
|
Y(z) = Z{X(s)}W(s)} = XW(z). |
Y(z) = Z{X(s)}W1(s)W2(s)} = XW1W2(z) |
||||||
Y(z,σ) = Z σ{X(s)W(s)} = XW(z,σ) Y(z,σ) = Zσ {X(s)}W1(s)W2(s)} = XW1W2(z,σ)
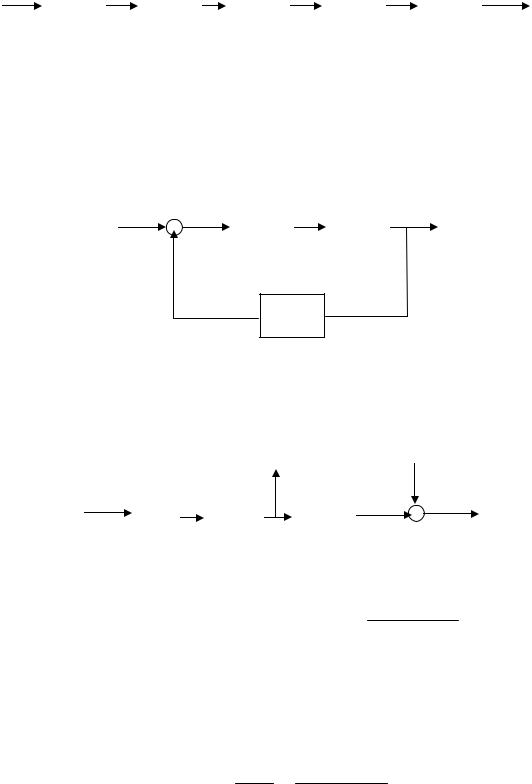
Правило 3. Z – изображение выходного сигнала группы звеньев, разделенных импульсными элементами, работающими синхронно и с одинаковым периодом квантования, равно произведению Z-форм передаточных функций отдельных звеньев.
144
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y(s) |
|
|
X(z) |
W1(s) |
|
|
|
|
|
|
W2(s) |
|
|
|
|
|
|
W3(s) |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Y(z) = X(z)W1(z)W2(z)W3(z), где |
W1(z) = |
Z{W1(s)}; W2(z) = Z{W2(s)}; W3(z) = |
||||||||||||||||||
= Z{W3(s)};
Выражение Y(z,σ) при σ ≠ 0 довольно сложное и здесь не производится. Пример: Простая система с одним импульсным элементом и неединичной обратной связью.
G(s) E(s) |
|
|
|
|
|
|
Y(s) |
||
|
|
|
|
|
W1(s) |
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W2(s)
Для записи выражения передаточных функций системы по управлению G(s) и ошибке E(s) разорвем искусственно систему (разрыв всегда делается перед импульсным элементом или перед первым импульсным элементом, если их несколько).
Y(s) G(s)
E(s) |
|
|
|
|
|
W1(s) |
|
W2(s) |
E(s) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем выражение для E(z)
1
E(z) = - E(z)W1W2(z) + G(z) = G(z)1+W1W2(z) .
Передаточная функция замкнутой системы по управлению
Фg(z)= |
Y (z) |
= |
|
W1 |
(z) |
|
. |
G(z) |
|
1+W W |
(z) |
||||
|
|
|
1 |
2 |
|
|
|
Передаточная функция замкнутой системы по ошибке:
Фe(z) = E(z) = + 1 .
G(z) 1 W1W2 (z)
Непосредственное применение правила Мэйсона к графу, эквивалентному структурной схеме дискретно-непрерывной системы, невозможно. Существует два пути использования правила Мэйсона для дискретно-непрерывных систем:
145
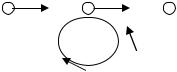
1) составление дискретного графа, в котором все переменные представлены дискретными величинами и для которого применение правила Мэйсона допустимо;
2) использования исходного эквивалентного графа с изменением формулы Мэйсона. Первый путь является более простым и эффективным и поэтому получил широкое распространение в практике анализа дискретно-непрерывных систем, особенно при решении задачи записи уравнений в Z-изображениях для систем сложной структуры с несколькими дискретными элементами.
В качестве иллюстрации использования формулы Мэйсона и записи уравнений в Z-изображениях рассмотрим простую дискретную систему с одним дискретным элементом и неединичной отрицательной обратной связью (рис. 2.23),
использованную выше для составления эквивалентного графа. |
|
|
|||||||
Уравнения для входа и выхода в изображениях |
|
|
|||||||
E(s) = G(s) - W(s)Wос(s)E*(s), Y(s) = W(s)E*(s). |
|
|
|||||||
Подвергнем Z-преобразованию записанные уравнения |
|
|
|||||||
E(z) = G(z) - WWос(z)E(z) = |
|
|
G(z) |
W (z) |
|||||
|
|
|
, Y(z) = W(z)E(z) = G(z) |
|
. |
||||
1+WW (z) |
1+WW (z) |
||||||||
|
|
|
|
|
ос |
ос |
|||
Составляем дискретный граф системы |
|
|
|||||||
G(z) 1 E(z) W(z) |
|
y(z) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
-WWос(z)
К такому графу правило Мэйсона применяется без всяких ограничений и условий:
Y (z) |
= |
|
W (z) |
; |
E(z) |
= |
|
1 |
. |
|
G(z) |
1+WW (z) |
G(z) |
1+WW (z) |
|||||||
|
|
|
|
|||||||
|
|
|
ос |
|
|
|
|
ос |
|
|
Передачи между непрерывными и дискретными сигналами могут быть определены из так называемого составного графа.
Составным графом называется совокупность дискретного и эквивалентного графов, полученная путем соединения выходных узлов квантователей эквивалентного графа с аналогичными узлами дискретно графа дугами с единичными передачами.
146
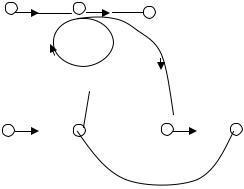
G(z) 1 E(z) W(z) Y(z)
-WWос(z) |
|
1 |
|
|
|
|
|
|
|
|
E(z)W1(s) |
||
G(s) |
|
E(s) |
|
|
|
Y(s) |
-Wx(s)
Составной граф для рассматриваемой нами системы будет следующим: Применение правила Мэйсона к составному графу позволяет записать выражения передач для всех непрерывных и дискретных вершин. Так например,
Y (s) |
= |
|
W1(z) |
; E(s) = G(s) - |
W1(s)Wос(s) |
G(z). |
|
G(z) |
1+WW (z) |
1+WW (z) |
|||||
|
|
|
|||||
|
|
|
ос |
|
ос |
|
|
5.5. Векторно-матричное описание
При переходе к дискретной аппроксимации непрерывной части системы будем считать, что входной сигнал квантуется с периодом Т, а затем преобразуется экстраполятором нулевого порядка.
Это значит, что внешнее воздействия U(t) остается постоянным в течение n- такта квантования, т. е. U(t) = u(nT), при nT ≤ t ≤ (n + 1)T.
Известно, что решением основного векторно-матричного уравнения непрерывной системы X =AX+BU является следующее выражение
t |
|
X(t) = Ф(t)X(o) + ∫Ф(t −τ)BU (t)dτ, |
(5.1) |
0 |
|
где Ф(t)= eAt - переходная матрица системы, имеющая форму матричной экспоненты eAt. Она вычисляется либо как сумма степенного ряда eAt = I +
+ At + |
A2 |
t2 |
+…+ |
Ak tk |
+…, либо как обратные преобразования Лапласа eAt = |
|
2 |
k ! |
|||||
|
|
|
|
= L-1{(SI - A)-1}.
Используем выражение (5.1) для определения вектора состояния во времени интервала nT≤t≤(n+1)T, считая начальными условиями x(nT), X(t) =
t
= Ф( - nT)X(nT) + u(nT) ∫Ф(t − τ)Bdτ. Для момента времени t = (n + 1)T имеем X[(n
0
147

(n+1)T
+ 1)T] = Ф(T)X(nT) + U(nT) ∫Ф[(n +1)T − τ]Bdτ, или после преобразований X(n +
nT
T
1) = Ф(T)X(n) + … + U(n) ∫[Ф(τ)dτ]B , где Ф(T) = eAT =L-1{(SI-A)-1} - - переходная
0
матрица непрерывной части системы при t = T.
T
Введем обозначения: A* = Ф(T); B*=[ ∫Ф(τ)dτ]B. Тогда векторно-матричное
0
описание дискретной системы будет иметь вид:
X(n + 1) = A*X(n) + B*U(n), Y(n) = CX(n) + DU(n).
По форме полученные уравнения являются полной аналогией векторноматричных уравнений непрерывной системы.
Векторно-матричное описание дискретной системы
Пусть дискретная система описывается передаточной функцией
b zq |
+ b zq−1 +... + b |
y(z) |
|
|||
W(z) = |
0 |
1 |
q |
= |
. |
|
|
|
|
|
|||
a0zq + a1zq−1 +... + aq |
u(z) |
|||||
Ей соответствует разностное уравнение |
|
|
|
|
||
a0y(n + q) + a1y(n + q - 1) +…+ aqy(n) = b0u(n + q) + b1u(n + q - 1) +…+ bqu(n). |
||||||
Переменные состояния примем следующие: |
|
|
|
|
||
|
|
X1(n) = y(n); |
|
|
|
|
X2(n) = x1(n + 1) = y(n + 1); |
|
|
||||
X3(n) = x2(n + 1) = y(n + 2); |
|
|
||||
……………………………… |
||||||
Xq(n) = xq-1(n + 1) = y(n + q - 1); |
||||||
|
Xq(n + 1) = y(n + q). |
|
|
|||
Подставим их в разностное уравнение, |
приняв a0 = 1, bq = 1, b0 = b1 = |
|||||
= … = bq-1 = 0, y(n+q) = xq(n+1) = - a1xq(n) - a2xq-1(n) -…- aqx1(n) + u(n).
Полученные уравнения можно представить в виде векторно-матричного
уравнения состояний: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x1(n +1) |
|
0 |
1 |
0 |
|
... |
0 |
|
x1 |
(n) |
|
0 |
|
||
|
|
|
|
|
|
|||||||||||
|
|
0 |
0 |
1 |
|
... |
0 |
|
|
|
||||||
|
x2 |
(n +1) |
|
|
|
x2 |
(n) |
|
0 |
|
||||||
|
= |
0 |
0 |
0 |
|
... |
1 |
|
+ |
u(n) |
||||||
|
... |
|
|
|
.... |
|
|
... |
||||||||
|
|
. |
. |
. |
|
... |
. |
|
|
|
||||||
|
xq |
(n +1) |
|
|
|
xq |
(n) |
|
1 |
|
||||||
|
|
− aq |
− aq−1 |
. − aq−2 |
|
... |
− a1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
148

Совместно с уравнением выхода
x1(n)
Y(n)=[10…0] ...x2 (n) . xq (n)
Вводя обозначения: X – вектор переменных состояния; А - матрица системы; В – матрица входа; С –матрица выхода; - записываем векторно-матричное уравнение дискретной системы в комплексной форме:
X(n + 1) = AX(n) + BU(n); Y(n) = CX(n).
Можно получить выражения матриц A,B и С и в более общем случае, когда bq ≠ 1 и b0 ÷ bq-1 ≠ 0 [1].
Решение дискретного уравнения состояния с помощью Z-преобразования
Рассмотрим дискретное уравнение состояния X(n+1)=A*X(n)+B*U(n), где
T
A* = eAT= L-1{(SI-A)-1}|t=T; B* = [ ∫Ф(τ)dτ]B. Подвергнем обе части уравнения со-
0
стояния Z-преобразованию zX(z) - zX(0) = A*X(z) + B*U(z). Отсюда X(z) = (zI - A*)- 1zX(0) + (zI - A*)-1B*u(z). Подвергая обратному Z- преобразованию, имеем X(n) = Z- 1{(zI - A*)-1z}X(0) + Z-1{(zI - A*)-1B*u(z)}. Покажем, что обратное Z – преобразование от (zI - A*)-1 есть дискретная переходная матрица состояния A(kT).
Z – преобразование A(kT) определяется общей формулой Z –преобразования A(z) =
∞−k
=∑ A(kT )z . Умножим обе части последнего уравнения на A*z-1 и вычтем ре-
k =0
зультат из последнего уравнения. Получим (I - A*z-1)A(z) = I, откуда A(z) = (I - A*z- 1)-1 = (zI - A*)-1z.
Вычисляя обратное Z – преобразование, получим A(kT) = Z-1{(zI-A)-1z}. Это выражение и является основой способа определения переходной матрицы состояния, основанного на Z – преобразовании.
Второе слагаемое в выражении для X(n) вычисляем с помощью теоремы свертки и выражение для A(kT);
k −1
Z-1{(zI - A*)-1B*U(z)} = ∑A[(k −i −1)T ]B(T )u(iT ).
i =0
149
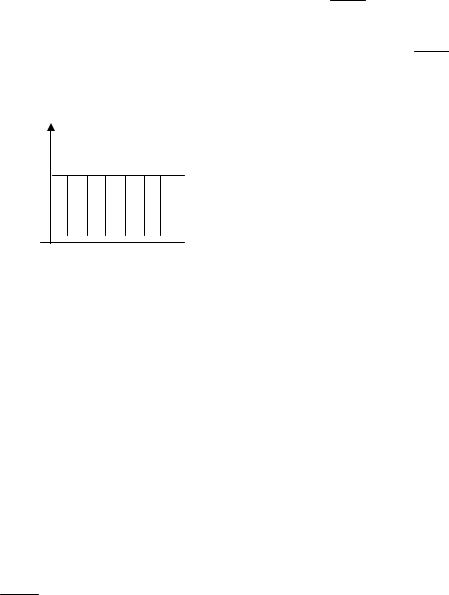
Полное переходное уравнение состояния
n−1
X(n) = A(n)X(0) + ∑A(n −i −1)BTu(i) .
i =0
Переходной характеристикой полностью дискретной системы называется реакция дискретной системы на единичную дискретную ступенчатую функцию.
Графическое представление входного сигнала и математическое описание дискретной ступенчатой функции имеет вид:
gи*(n) = 1, n ≥ 0; gи*(n) = 0, n < 0.
Z – преобразование дискретного входного сигнала Gи(z) = z z−1.
Z – преобразование переходной характеристики H(z) = D(z)Gи(z) = z z−1D(z), где
D(z) – дискретная передаточная функция дискретной системы. Таким образом, h(n) = Z-1{D(z)}.
g*и
1
0 1 2 3 4 5 6 n
5.6. Частотные характеристики
Построение ЛАФЧХ дискретных систем и отдельных звеньев имеет свои характерные особенности. Они следуют из того факта, что выражения модуля и фазы КПФ дискретной системы являются функциями ejωT и не логарифмируются непосредственно. Кроме того, диапазон частот дискретных характеристик 0 ≤ ω ≤ π/T не распространяется на всю ось абсцисс ЛАФЧХ непрерывных систем. Чтобы сделать выражения модуля и фазы логарифмируемыми и привести диапазон частот к подобному диапазону ЛАФЧХ непрерывных систем предварительно выполняется преобразование выражения ПФ дискретной системы с помощью
подстановки z =11+− ww . Эта подстановка называется w-преобразованием. Чтобы
выяснить, как новая переменная w связана с обычной частотой ω, используем связь z = ejωT. Из формулы w-преобразования определяем
150

|
|
|
|
w = |
z −1 |
= |
e jωT |
−1 |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
e jωT |
|
|
|
|
|
|||||||
|
|
|
z +1 |
+1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Используя формулу Эйлера ejα = cosα + jsinα, имеем |
|
|
|
||||||||||||||||
|
w = |
cosωT + j sinωT −1 |
= |
(cosωT + j sin ωT −1)(cosωT − j sin ωT +1) |
= |
|
|||||||||||||
|
|
cosωT + j sin ωT +1 |
|
|
|
|
(cosωT +1)2 + sin2 ωT |
|
|||||||||||
= |
cos2 |
ωT + j sinωT cosωT − cosωT − j sinωT cosωT + sin |
2 ωT + j sinωT + |
= |
|||||||||||||||
|
|
cos2 ωT + 2cosωT +1+ sin2 ωT |
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
+ |
cosωT + j sinωT −1 |
|
|
|
|
= |
|
2 j sinωT |
= jtg ωT . |
|
|||||||
|
|
cos2 ωT + 2cosωT +1+ sin2 |
|
|
|
|
2(cosωT +1) |
|
|||||||||||
|
|
|
ωT |
|
2 |
|
|
||||||||||||
Окончательно имеем w = jtg ωT = j |
|
, где |
|
|
= tg ωT так называемая относитель- |
||||||||||||||
λ |
λ |
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
ная псевдочастота. Нетрудно заметить, что при 0 ≤ ω ≤ π/T относительная псевдочастота будет меняться в диапазоне 0 ≤ λ ≤ ∞, т. е. Частотные характеристики дискретных систем, построенные в функции λ, будут подобны характеристикам непрерывных систем. На практике частотные характеристики дискретных систем строятся в функции не относительной, а абсолютной псевдочастоты λ = (2/T) λ. Дело в том, что при малых ω (область низких частот) имеем
λ = tg ω2T ≈ ω2T , а λ = T2 λ ≈ T2 ω2T = ω.
Это значит, что характеристики дискретных систем в области низких частот будут совпадать с характеристиками приведенной непрерывной части.
Посмотрим, как строятся ЛАФЧХ дискретных рассмотренных выше динамических звеньев: интегрирующего и апериодического 1-го порядка.
В ПФ дискретного интегратора W (z) = zkT−1 вводим подстановку z =11+− ww :
|
|
|
W (w) = |
|
|
kT |
|
|
= kT 1− w . |
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
+ w |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
w |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1− w |
|
|
|
|
|
|
|
|
|
|
|
|||||
Далее принимаем w = j(T/2)λ и получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
W ( jλ) = kT |
1 |
− jT |
2 |
λ |
= k |
1− jT |
2 |
λ |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
|
|
jT 2λ |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
jλ |
|
|
|
|
|
|
|
|
||||
Выражение ЛАЧХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L(λ) = 20lg |
|
k |
1− jT |
2 |
λ |
|
= 20lgk |
− 20lgλ + 20lg 1+ |
T |
2 |
λ |
2 |
. |
||||||||||
|
|
||||||||||||||||||||||
|
jλ |
|
|
|
|
|
4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
151

Выражение ЛФЧХ
ϕ(λ) = − arctg(T/2)λ − π/2.
Графики ЛАФЧХ интегрирующего звена показаны на рис. 5.10.
− 20 дБ/дек
ϕ, …°
 L(λ) 20 lgk
L(λ) 20 lgk
|
|
|
|
1 |
|
|
λ |
|
|
|
|||||
|
|
|
|
|
|
|
− 90 |
|
|
|
ϕ(λ) |
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 180 |
|
|
|
|
|
|
|
|
Рис. 5.10
Из графиков видно, что в области низких частот ЛАФЧХ дискретного интегратора совпадают с ЛАФЧХ непрерывного интегрирующего звена (наклоном –20 дБ/дек, фазовый сдвиг ϕ = −π/2. Существенное отличие характеристик имеет место в области высоких частот (нулевой наклон и фазовый сдвиг ϕ = − π).
|
Перейдем к апериодическому звену 1-го порядка. Эквивалентная схема дис- |
||||||||||||||||||||||||||||||||||
кретного апериодического звена имеет вид (рис. 5.11). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретная передаточная функция апериодиче- |
||||||||||||||
g |
|
|
|
|
|
|
1−e−sT |
|
k |
|
|
|
|
|
y |
ского звена |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
s |
|
T1s +1 |
|
|
|
|
|
|
−sT |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − e |
|
|
|
k |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Рис. 5.11 |
|
|
|
|
|
|
|
|
|
Wa (z) = Z |
|
|
|
|
|
|
|
|
|
= |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
T s + |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
= k(1− z−1)Z |
|
|
|
|
|
. Для определения Z |
|
|
|
|
предварительно разло- |
||||||||||||||||||||||||
s(T s +1) |
s(T s +1) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
жим |
1 |
|
|
|
|
на сумму простых слагаемых: |
|
|
1 |
|
|
= 1 |
− |
|
1 |
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
s(T1s +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(T1s +1) |
s |
|
|
|
s + 1T |
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
. Подставляем в общую формулу Wa(z): |
|||||||||||||||||||||
Тогда Z |
|
− |
|
|
|
|
= |
|
|
|
|
|
− |
|
|||||||||||||||||||||
|
|
+ 1T |
|
|
|
|
|
−T T1 |
|||||||||||||||||||||||||||
|
|
|
s |
|
|
s |
|
|
|
z −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
z −e |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
152
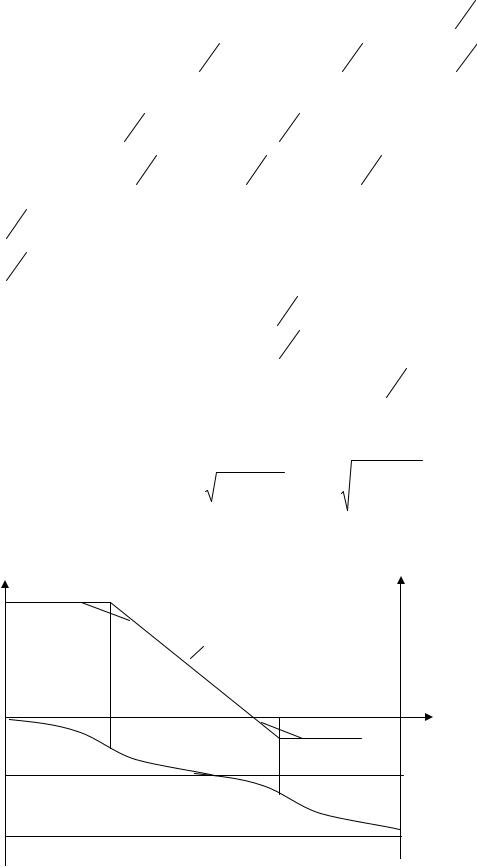
|
|
|
|
|
|
z −1 |
|
|
|
z |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
z −1 |
|
|
|
|
|
|
−T T |
||||||||
|
W |
|
(z) = k |
( |
|
− |
|
|
|
|
) = k(1− |
|
) = k |
1− e |
1 |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
a |
|
|
|
z |
|
|
|
z −1 z − e−T T1 |
|
|
|
|
z − e−T T1 |
|
|
|
z − e−T T1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Переходим к w-преобразованию Wa(z): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−T T |
|
|
|
|
|
(1 |
|
−T T |
|
|
|
|
|
|
|
|
|
1− w |
|
|
||||||||
|
W (w) = k |
(1− e |
|
|
1 ) |
|
= k |
|
− e |
|
|
1 )(1− w) |
|
|
= k |
, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
a |
|
|
|
|
1+w |
|
|
−T |
T1 |
|
|
|
|
|
−T |
|
|
|
|
|
|
−T |
|
|
|
|
|
1+ cw |
|
|
||||||||
|
|
|
|
|
|
|
|
− e |
|
|
|
(1− e |
|
T1 ) + w(1+ e |
T1 ) |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1−w |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1+ e |
−T T |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где c = |
|
|
1 |
= cth |
|
. Подставим w = j(T/2)λ в выражение Wa(w): |
|
|
|||||||||||||||||||||||||||||||||
|
−T |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1− e |
T1 |
|
|
|
|
2T1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W ( jλ) = k |
1− jT |
|
2 |
λ |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
1 |
+ cjT |
2 |
λ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− jT 2λ |
|
|
|
|
|
||||||
Можно доказать, что |
lim |
cT |
=T . Поэтому W |
( jλ) k |
. |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
T →0 |
2 |
|
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
|
1+T1λ |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Переходя к ЛАФЧХ, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
L (λ) = 20lgk − 20lg |
1+T 2λ2 |
|
+ 20lg |
1+ |
T 2λ2 |
|
, |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ϕa(λ) = − arctg(T/2)λ − arctgT1λ.
Графики Lа(λ) и ϕa(λ) показаны на рис. 5.12.
ϕ, …°
|
L |
|
|
|
|
1 |
1 |
|
T1 |
|
T |
λ
− 90
−
Рис. 5.12
Как и для интегрирующего звена, так и для апериодического звена 1-го порядка наблюдается совпадение ЛАФЧХ в области низких частот и существенное
153
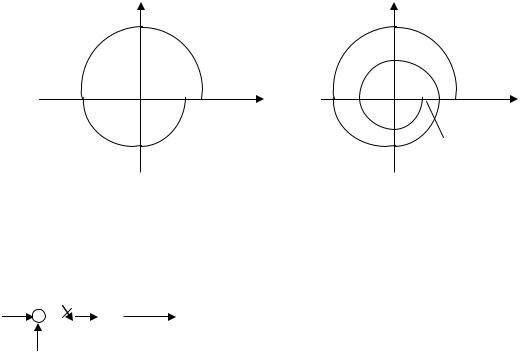
различие в области высоких частот для непрерывного и дискретного режимов работы.
Аналогично описанному выше строятся ЛАФЧХ других дискретных звеньев и систем. Свойство совпадения ЛАФЧХ в области низких частот сохраняет свою силу и для других более сложных звеньев и систем, что позволяет использовать для дискретных систем методы анализа и синтеза, разработанные для непрерывных систем.
Отметим, что для сложной передаточной функции непрерывной части дис- кретно-непрерывной системы построение ЛАФЧХ может быть выполнено приближенным способом , допускающим полное совпадение характеристик непрерывной и дискретной системы в области низких частот
0 ≤ λ < 2/T.
5.7. Устойчивость систем
Для устойчивости замкнутой дискретной системы необходимо и достаточно, чтобы при изменении частоты в диапазоне 0 ≤ ω ≤ π/T годограф характеристического полинома обошел в положительном направлении 2n квадрантов, нигде не обращаясь в нуль и не пересекаясь сам с собой.
ImD(ejωT) |
n = 2 |
ImD(ejωT) |
n = 4 |
|
|
|
|||
|
|
|
|
|
|
ω=π/T |
|
|
|
0 |
ω = 0 ReD(ejωT) |
0 |
ω = 0 ReD(ejωT) |
|
|
|
|
|
ω=π/T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.13 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Годографы устойчивых дискретных систем второго и четвертого порядка |
||||||||||||||||||||||||||||||
показаны на рис. 5.13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Как и отмечалось ранее, крайние точки годографов D(ej 0) и D(ej π) являются |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вещественными и находятся на вещественной оси. |
|||||||||||||||
|
g(t) |
|
|
|
|
|
|
y(t) |
|
|
|
В качестве примера построим годограф для дис- |
||||||||||||||||||||
|
k |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
s |
|
|
|
|
|
|
|
кретного интегрирующего звена в системе с отрицатель- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной обратной связью (рис. 5.14). |
|
|
|
|
|
|||||||||||
|
|
|
|
|
Рис. 5.14 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Передаточная функция разомкнутой системы |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−sT |
|
|
−1 |
|
1 |
|
z −1 Tz |
|
|
kT |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1−e |
|
|
k |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
W (z) = Z |
|
|
|
|
|
|
= k(1− z |
|
)Z |
|
|
= k |
|
|
|
|
= |
|
|
. |
||||||
|
|
s |
|
|
2 |
z |
|
|
2 |
z −1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
s |
|
|
(z −1) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
154

Передаточная функция замкнутой системы |
|
|
|||||||||
Ф(z) = |
W (z) |
|
kT |
|
|
||||||
|
= |
|
|
|
. |
|
|
|
|
|
|
1 + W (z) |
z − 1 + kT |
|
|
||||||||
Характеристический полином замкнутой системы |
|
|
|||||||||
D(z) = z + kT – 1 = a0z + a1, |
ImD(ejωT) |
|
|
||||||||
где a0 = 1; a1 = kT – 1. Полагаем z = ejωT при |
|
|
|
|
|
|
|
|
|
||
0 ≤ ω ≤ π/T. D(ejωT) = a0 ejωT + a1. График |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
a0 |
|
|
|||
D(ejωT) показан на рис. 5.15. Он представля- |
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
ω = 0 ReD(ejωT) |
|||||
ет собой полуокружность радиуса a0 = 1 и с |
|
|
a1 |
|
|||||||
|
ω=π/T |
||||||||||
центром в точке a1 = kT – 1. |
|
|
Рис. 5.15 |
|
|
||||||
|
|
|
|
|
|
|
|||||
5.8. Анализ качества
Перейдем к дискретно-непрерывной системе и покажем, как определяются коэффициенты ошибок на примере типовой одноконтурной системы с одним дискретным элементом. Как и для непрерывной системы рассмотрим установившиеся ошибки при отработке трех типовых воздействий: g(t) = g01(t), g(t) = g0t1(t),
g(t) |
= |
|
|
g0t21(t). Передаточная |
функция замкнутой системы по ошибке |
|||
Фeg (z) = |
|
|
1 |
, где W1W2 |
(z) |
= Z{W1(s)W2(s)}.. |
||
1 |
+W1W2(z) |
|||||||
|
|
|
|
|
||||
1. Внешнее воздействие g(t) = g01(t). Его Z-изображение G(z) = g0 z z−1.
Z-изображение ошибки E(z) = g0 |
|
z |
|
|
1 |
|
. |
|
|
|
|
|||||||||||||
z −11+W W (z) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
Установившееся значение ошибки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
e(n) = lim |
z −1 |
E(z) = lim |
z −1 |
g |
|
z |
|
|
1 |
|
|
g0 |
|
. |
||||||||||
|
|
0 z −11+W W (z) 1+ lim W W |
(z) |
|||||||||||||||||||||
n→∞ |
|
z→1 |
z |
z→1 |
z |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
z→1 1 2 |
|
|
|
Пусть lim W W |
2 |
(z) = k |
- общий коэффициент передачи разомкнутой системы. |
|||||||||||||||||||||
z →1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда e(n) = |
|
g0 |
= C0g0; |
C0 = |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1+ k |
1+ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
С0 – коэффициент ошибки по положению. Он определяется таким же, как и для непрерывной системы, выражением. Из выражения для ошибки видно, что чтобы С(∞) = 0, коэффициент передачи должен быть бесконечным. Это будет иметь место, если W1W2(z) содержат хотя бы один полюс z = 1. Например, в составе
155

W1W2(z) имеется передаточная функция дискретного интегратора W (z) = zkT−1.
Тогда lim W W (z) = ∞. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
z→1 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2. Внешнее воздействие g(t) = g0t1(t), G(z) = |
|
|
|
g0Tz |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
(z −1)2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Изображение ошибки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
E(z) = G(z)Фeg |
(z) = g0 |
|
Tz |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
. |
|
||||||||||||||
|
|
|
|
|
|
|
(z −1) |
2 |
|
1 |
|
+W W (z) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
||||||||||
Установившиеся значение ошибки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
e(n) = lim |
z −1 |
E(z) = lim |
z −1 |
g0 |
|
|
Tz |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
= |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
1 |
+W W |
(z) |
|
|||||||||||||||||||||||||||||||
|
|
n→∞ |
z |
→1 |
z |
|
|
|
z→1 |
z |
|
(z − |
1) |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
||||||||||
|
|
= lim |
|
|
g0T |
|
|
|
|
|
= |
|
|
|
|
|
g0 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
g0 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
z→1 |
(z |
−1)[1+W1W2(z)] |
|
|
|
lim |
z −1 |
W1W2(z) |
|
|
lim (z −1)W1W2(z) |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z→1 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T z→1 |
|
|
|
|||||||
Определим коэффициент ошибки по скорости как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
C = |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
= |
|
1 |
, |
C |
= |
|
1 |
, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
lim (z −1)W1W2(z) |
|
|
kν |
|
1 |
|
|
|
kν |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
T z→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где k |
ν |
= |
1 |
lim (z −1)W W (z) − добротность системы по скорости. Для системы |
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
|
T z→1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
астатической 1-го порядка, передаточная функция которой содержит один полюс z = 1, kν = k/T. Для того чтобы установившееся значение ошибки было равно нулю, необходимо, чтобы C1 = 0, т. е. kν = ∞. Это возможно, если W1W2(z) имеет два полюса z = 1.
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
G(z) = g0 |
T |
2z(z +1) |
|
|
|
|
|||||
3. Внешнее воздействие g(t) = g0t 1(t), |
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||
|
2(z −1)3 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Изображение ошибки E(z) = g |
0 |
T 2z(z +1) |
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|||||||||||
|
2(z −1) |
3 |
1 |
+W W (z) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
||
Установившееся значение ошибки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
e(n) = lim |
z −1 |
E(z) = lim |
z −1 |
g0 |
T 2z(z +1) |
|
1 |
|
|
|
|
= |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||
|
z |
|
|
|
z |
|
|
|
2(z −1) |
1+W W |
|
(z) |
||||||||||||||||
n→∞ |
z→1 |
|
|
|
|
|
|
z→1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|||||||
|
T 2 |
|
|
|
z +1 |
|
1 |
|
|
|
|
|
|
g T 2 |
|
|
|
|
|
|
||||||||
= |
|
|
g0 lim |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
0 |
|
|
|
|
|
|
= |
|
|
2 |
|
|
|
|
2 1+W W (z) |
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
z→1 |
(z −1) |
|
lim (z −1) |
W W (z) |
|
||||||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z→1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
156
|
|
|
|
= |
|
|
|
|
|
g 0 |
|
|
|
= |
g 0 |
= C 2 g 0 ; |
C 2 = |
1 |
, |
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
lim |
|
|
(z − |
1) |
2 W W |
2 |
(z) |
k a |
|
k a |
||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
z →1T 2 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где k |
a |
= |
1 |
lim (z −1) |
2W W (z) − добротность системы по ускорению. |
||||||||||||||||
|
|||||||||||||||||||||
|
T 2 z→1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из выражения e(n) |
= g0 |
1 |
|
видно, что установившаяся ошибка будет равна ну- |
|||||||||||||||||
ka |
|
||||||||||||||||||||
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лю, если ka = ∞, т. е. W1W2(z) иметь три полюса z = 1.
Замечание. Полученные выражения C1 и C2 справедливы только тогда, когда внешние сигналы g(t) представляют собой скачки скорости и ускорения соответственно.
Вопросы для самопроверки
1.Сформулируйте определение дискретных систем. Какова структура и классификация импульсных систем?
2.Расскажите о математическом аппарате исследования импульсных систем.
3.Сформулируйте теорему Котельникова-Шеннона. Поясните ее физический смысл и практическое значение при проектировании дискретных систем.
4.Поясните методы определения передаточных функций импульсных систем. Каковы особенности передаточных функций статических и астатических систем?
5.Каким образом определяются частотные характеристики импульсных систем?
6.Какими способами определяются переходные процессы в дискретных системах?
7.Сформулируйте условия устойчивости импульсных систем.
8.Каким образом оценивается точность работы импульсных систем?
9.Каков порядок синтеза цифровых систем? Перечислите методы определения передаточных функций корректирующих устройств. Укажите виды структурных схем цифровых фильтров.
10.Запишите стандартную форму уравнений в пространстве состояний. Поясните физический смысл уравнений.
157
