Первичные изм. преобразователи. Часть 1

2.4. Датчик линейных перемещений и угла поворота

Характер деформаций при изгибе. Основные допущения

При изгибе, как и при растяжении или сжатии, необходимо в ряде случаев решать задачи об определении деформации балки как целого или определять перемещения отдельных ее точек.

Водних случаях это вызывается тем, что по условиям работы конструкции в элементах ее не допускаются перемещения, превышающие некоторые заданные значения. Так в точном машиностроении, чтобы не нарушить «точности» работы механизмов, величины деформаций строго лимитируются.

Вдругих случаях определение перемещений не является самоцелью, но они дают возможность рассчитать статически неопределимые системы. С этим мы уже имели дело при расчетах на растяжение— сжатие не статически неопределимых систем.

Рис. 2.4.1. Определение деформаций при изгибе

Рассмотрим общую идею метода определения деформаций при изгибе на примере простой балки, опирающейся на дне опоры (рис. 2.4.1). Характерной особенностью деформации изгиба по сравнению с растяжением и сжатием является то, что ось балки, прямая до деформации, превращается под действием нагрузки в кривую, которая называется

90

упругой линией балки. Задача о деформации балки будет решена, если нам станет известно математическое уравнение упругой линии.

Из математики мы знаем, что каждая кривая характеризуется в данной ее точке тремя дифференциально связанными между собой величинами:

1) ординатой

2) тангенсом угла наклона касательной, который носит название угла

Применительно к балке, для которой координатную ось х совмещаем с геометрической осью балки, ординату z будем называть прогибом балки в данной точке (отрезок CC1), а угол θ — углом поворота в данном сечении. Заметим, что угол поворота — это угол между нормалью к оси балки в данной точке до и после деформации или угол, на который поворачивается плоскость данного поперечного сечения балки, так как предполагаем, что поперечные сечения и после деформации нормальны к оси балки в соответствующих точках.

Прогиб и угол поворота являются теми перемещениями, которые приходится вычислять при практических расчетах. Деформация балки зависит от двух факторов:

1.От деформаций продольных волокон, обусловленных действием нормальных напряжений, вызываемых изгибающим моментом Мy

2.От сдвигов, вызываемых действием касательных напряжений, зависящих от поперечной силы Qz.

91

Исследования показали, что влияние касательных напряжений и следовательно, поперечных сил на деформацию изгиба весьма мало, поэтому они, как правило, не учитываются, и деформации исследуются только от действия изгибающих моментов.

На рис 2.4.1 пунктиром показана ось балки после деформации, то есть ее

упругая линия. Опытное изучение деформации балок при изгибе в пределах упругости показало, что упругая линия является плавной и непрерывной кривой. Математически это означает, что ни в одной точке кривой функция

z(х),г так же ее производная dz не претерпевают разрыва.

dx

Произвольная точка оси, строго говоря, перемещается не вертикально (не по нормали к первоначальной оси балки), а по некоторому наклонному направлению за счет горизонтального перемещения шарнирно-подвижной опоры. Эти перемещения являются величинами второго порядка малости по сравнению с вертикальными перемещениями, что позволяет ими пренебречь и учитывать лишь вертикальные перемещения.

Уравнения (2.4.1) — (2.4.3) характеризуют чисто геометрическую сторону явления и не устанавливают связи упругой линии с нагрузкой и с внутренними силами.

Вполне очевидно, что очертание упругой линии находится в прямой зависимости от действующих на балку сил. Если бы нам удалось одну из

трех геометрических характеристик z, θ и ρ1 связать с внешними или

внутренними силами, то, пользуясь дифференцированием или интегрированием, можно было бы найти и две другие характеристики.

Основное дифференциальное уравнение упругой линии

С установлением связи между деформациями и внутренними силами при изгибе мы столкнулись при выводе формулы для нормальных напряжений

σ = M y z . IY

92

Зависимость кривизны в данной точке оси от изгибающего момента Му и жесткости балки при изгибе Е1у, получим:

В указанной зависимости кривизна и изгибающий момент являются

Для удобства дальнейших операций необходимо принять такое правило

знаков для кривизны 1 ,при котором ее знак будет всегда совпадать с

ρ x

принятым нами знаком изгибающего момента в том же сечении. Это приводит нас к правилу, согласно которому кривизна положительна, если упругая линия в данной точке обращена выпуклостью вниз (тот же знак мы имеем и для изгибающего момента). В соответствии с этим условием в дальнейшем направим ось z вверх. Приравняем левые части зависимостей

( ) и (2.4.3) и получим дифференциальное уравнение упругой линии в виде:

Для изучаемых нами малых деформаций можно пренебречь в знаменателе величиной квадрата первой производной* по сравнению с единицей, и тогда получим так называемое приближенное дифференциальное уравнение упругой линии

Малые упругие деформации позволяют упростить зависимость (2.4.2), так как можно положить, что

Углы поворота θ ≈ dz в пределах упругости выражаются (в радианах) очень малой dx

правильной дробью

93

Резюмируя вышеизложенное, можно принять следующие правила знаков:

1.Прогиб считается положительным, если он направлен вверх.

2.Угол поворота считается положительным, если касательная к упругой линии в данной ее точке, параллельно перенесенная в начало координат, проходит в нечетных квадрантах координатной системы.

Исследование деформаций балок с одним грузовым участком

Перейдем к практическому использованию приближенного дифференциального уравнения упругой линии и рассмотрим эту задачу в общем виде.

Интегрируя уравнение (2.4.5), получим

Интегрируя выражение угла поворота (2.4.8), получаем уравнение упругой линии z = f(x)

В выражениях (2.4.8) и (2.4.9) С и D являются произвольными постоянными. Эти интегрирования возможны, если изгибающий момент Му является непрерывной функцией от х, то есть Му = f(x), что, как мы знаем, имеет место лишь в пределах одного грузового участка. Поэтому число дифференциальных уравнений будет равно числу грузовых участков балки. Для каждого такого участка мы получим при интегрировании две произвольные постоянные, и, таким образом, если балка имеет n грузовых участков, то число произвольных постоянных будет 2n.

Из математики известно, что произвольные постоянные не влияют на

94

очертание кривой, выражающей найденную функцию, но определяют положение этой кривой в принятой системе координат. Это обстоятельство дает нам способ для определения постоянных интегрирования, при которых упругая линия займет то положение, которое диктуется характером закрепления балки на ее опорах и при котором сопряжение отдельных кривых на границах грузовых участков будет удовлетворять условиям плавности и непрерывности. Этих условий бывает достаточно, чтобы составить 2п уравнений для определения 2п постоянных интегрирования. Все высказанные соображения будут разъяснены ниже при рассмотрении частных случаев.

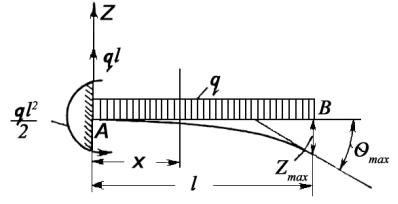
Сначала рассмотрим балку, защемленную одним концом, с одним грузовым участком и нагруженную равномерно распределенной нагрузкой, интенсивностью q (рис. 2.4.2).

Рис. 2.4.2

Начало координат поместим в защемленном конце, ось х направим вправо. Значения опорных реакций в защемлении указаны на рисунке. Напишем выражение для изгибающего момента в сечении х.

Дифференциальное уравнение упругой линии в этом случае напишется в виде:

95

Интегрируя это уравнение последовательно два раза, получим

Для определения произвольных постоянных С и D воспользуемся условиями закрепления балки. В защемленном конце балки, как известно, прогиб и угол поворота равны нулю. Эти условия математически можно

После использования указанных граничных условий в зависимостях (2.4.11) и (2.4.12) получим, что произвольные постоянные равны нулю, то есть С = 0 и D = 0. После подстановки этих значений в те же уравнения (2.4.11) и (2.4.12) получим окончательные выражения углов поворота и прогиба для любого сечения

Последнее уравнение показывает, что для рассматриваемого случая упругая линия изменяется по закону параболы четвертой степени.

Упругую линию можно построить по ординатам z(x) для ряда значений х. Задача несколько упрощается, если выражение для прогиба

представить в функции относительных (безразмерных) абсцисс ξ =

этой цели в уравнении (2.4.14) вынесем за скобки ql 4 , тогда получим

24

и окончательно

96

24EI y

Таблица2.3

Разобьем пролет l на пять равных частей через 0,2l и подсчитаем величину алгебраического выражения в скобках уравнения (2.4.15). Эти значения помещены в табл.2.3. Истинные значения прогибов могут быть получены

относительными (безразмерными) координатами данные табл.2.3 действительны для любых заданных значений l, q и Е1у. По данным этой таблицы на рис. 2. 4.3 построена упругая линия балки.

Наибольший практический интерес обычно представляют максимальные значения углов поворота и прогибов. Эти значения для нашего примера будут на свободном конце, то есть при х= l (ξ=1). Имеем

97

получим

C = θ0 и D = z0.

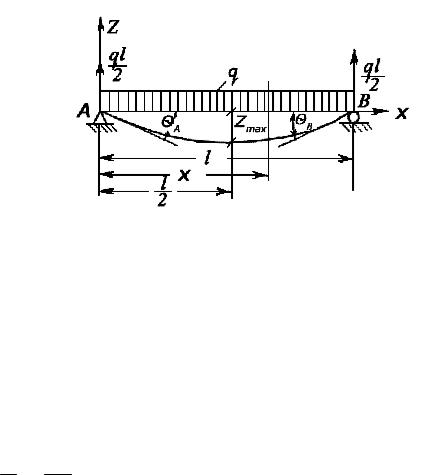
Рис. 2.4.4

Рассмотрим в качестве второго примера балку, опирающуюся на две шарнирные опоры и наружную равномерно распределенную нагрузку интенсивностью q. На рис.2.4.4 приведены все необходимые данные, а также значения опорных реакций. Балка имеет один грузовой участок. Изгибающий момент для произвольного сечения х будет

M y = ql x − qx2

2 2

и на основании (2.4.5) запишем дифференциальное уравнение упругой линии в таком виде:

99