3.2. Связь бесконечно малых и бесконечно больших величин

Если ч.п. является бесконечно малой и нигде ее члены в ноль не обращаются, то очевидно ч.п.является бесконечно большой. И - наоборот.

3.3. Типы неопределенных выражений

В случаях, когда теоремы о пределе суммы или разности, произведения или частного оказываются не применимыми, говорят о наличии неопределенности в выражении, стоящем под знаком предела. К ним относят следующие неопределенные выражения:

1. неопределенность типа , когда вычисляется предел отношения, в котороми- бесконечно малые величины;

2. неопределенность типа , когда вычисляется предел отношения, в котороми- бесконечно большие величины;

3. неопределенность типа , когда вычисляется предел произведения, в которомбесконечно малая а- бесконечно большая величина;

4. неопределенность типа , когда вычисляется предел разности, в котороми- бесконечно большие величины. Помимо них встречаются неопределенности типови.

Для вычисления этих пределов применяют различные приемы раскрытия неопределенных выражений. В частности используют теорему о том, что если , то.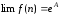

При вычислении пределов используют следующую классификацию б. м. величин.

Если , тосчитают величиной более высокого порядка малости по сравнению си пишут.

Если (), то величиныисчитают величинами одного порядка малости.

Если , то величиныисчитают эквивалентными. Одну эквивалентную величину можно заменять на другую в произведениях и частном.

Аналогичным образом осуществляют сравнение бесконечно больших величин.

Для раскрытия неопределенных выражений типа применяют теорему Штольца.

Теорема (Штольца). Пусть числовая последовательность является возрастающей бесконечно большой величиной, а- бесконечно большая величина. Тогда выполняется соотношение

,

если только существует предел справа (конечный или бесконечный).

В зависимости от сравниваемых числовых последовательностей ипредел может быть конечным числом, нулем, или не существовать.

Примеры.

1. ,. Тогда- конечное число.

2. ,. Тогда.

3. ,. Тогда.

4. ,. Тогда- не существует.

5. ,. Тогда.

6. ,. Тогда.

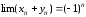7. ,. Тогда- не существует.

4. Число

Особое место в математике занимает число . Оно определяется как предел числовой последовательности

(1)

Для анализа характера изменения членов числовой последовательности воспользуемся формулой бинома Ньютона

,

(2)

где - число сочетаний изэлементов по.

Применим формулу (2) к соотношению (1). В результате получим

. (3)

Таким образом, получено, что

. (4)

Оценим сверху члены числовой последовательности

.

Последнее соотношение есть сумма членов геометрической прогрессии с первым членом и знаменателем. Поэтому

.

Итак, последовательность (1) ограничена сверху. Она является также возрастающей. Действительно, из формулы (3) видно, что для следующего члена последовательности число положительных слагаемых возрастет на единицу и каждое слагаемое, начиная с третьего увеличится. Возрастающая, ограниченная сверху последовательность имеет предел

.

Для оценки числа выполним следующие рассуждения. В (3) отбросим последние члены суммы

.

В последнем соотношении перейдем к пределу

.

Заменяя в последнем соотношении индекс наи с учетом неравенства (14) получаем

.

С учетом теоремы о сжатой переменной получаем важное соотношение

. (5)

Именно оно позволяет вычислить число с любой заданной точностью. При этом пользуются следующим соотношением

, (6)

где .

Число 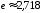. Оно используется как основание натуральных логарифмов и записывается в виде

.

Известно, что формула перехода от основания к основаниюлогарифмов имеет вид

.

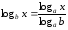Если и, получим

.

Если и, получим

.

1B.Bolzano- чешский математик,A.L.Cauchy- французский математик

13