Расчёт управляющего воздействия нечёткого регулятора

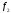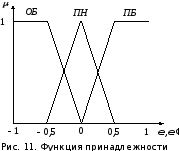
Необходимо рассчитать компенсирующее воздействие нечёткого компенсатора u₂для случая, когда= 0,1 и=f₁^’=0,3. Функция принадлежности возмущающего сигнала f и его первой производной f^/приведена на рисунке 11. Упрощённый алгоритм нечёткого управления представлен следующим правилом:

Правило №1: Если f= ПН Иf^’= ПБ, тогдаU_к= ОБ;

Правило №2: Если f= ОБ ИЛИf^’= ПБ, тогдаU_к= ПН.

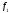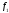Еслисчитать, что= 0,25 есть ОБ, то по функции принадлежности находим степень принадлежностик ОБ: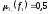. (см. приложение 3)

Если считать, что = 0,3 есть ПН, то по функции принадлежности находим степень принадлежностик ПН:.

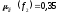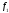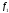Если считать, что = 0,25 есть ОБ, то по функции принадлежности находим степень принадлежностик ОБ:.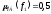

Если считать, что 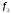= 0,3 есть ПБ, то по функции принадлежности находим степень принадлежности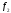к ПБ:.

На основании правила Мамдани т.к между 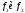стоит союзИ, то усекаем функции принадлежности на min на уровне, а если между парами стоит союзИЛИ, усекаем функцию принадлежности управляющего воздействияна max уровне. Полученное нечеткое множество представлено заштрихованной фигурой.

Дефаззификацию выполним по методу центра тяжести. В соответствии с ним, чёткое управляющее воздействие есть абсцисса центра тяжести полученной фигуры .

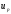Заключение

В данной работе выполнен синтез комбинированной САУ техническим объектом, заданным в форме экспериментальных переходных характеристик. Произведен выбор математической модели объекта управления в форме передаточных функций по управляющему и возмущающему каналам, выбран ПИ алгоритм управления и произведен расчет параметров ПИ-регулятора графоаналитическим методом. Рассчитан физически реализуемый компенсатор, обеспечивающий компенсацию возмущений. Построены кривые переходных процессов в системе и определены показатели качества. Осуществлен переход от аналогового (непрерывного) регулятора к НЦУ. Построена САУ с использованием методов нечёткой логики. Рассчитано компенсирующее воздействие нечёткого компенсатора.

Список используемой литературы

1. Лукас В.А. Основы теории автоматического управления. Л.: Недра, 2005г.

2. Медведев Р.Б., Бондарь Ю.Д., Романенко В.Д. АСУ в металлургии. М.: Металлургия, 1987г.

3. Марюта А.Н., Качан Ю.Г., Бунько В.А. Автоматическое управление технологическими процессами обогатительных фабрик. М.: Недра, 1983г.

4. Ротач В.Я. Теория автоматического управления. М.: Издательство МЭИ, 2004.

5. Ротач В.Я., Шавров А.В., Бутырев В.П. Синтез алгоритмов машинного расчета оптимальных параметров систем регулирования. М.: Теплоэнергетика, 1978, №12.

Приложение 1

Рис.1.График экспериментальной переходной характеристики по управляющему каналу

Рис.2.График экспериментальной переходной характеристики по возмущающему каналу