
- •Курсовой проект
- •Содержание.
- •Аннотация.
- •Annotation.
- •Введение.
- •Задание.
- •1. Получение математической модели объекта в виде передаточной функции.
- •Модель 2
- •Модель 4
- •Модель 6
- •Модель 7
- •Погрешность аппроксимации
- •Модель 6
- •Модель 7
- •Погрешность аппроксимации
- •2. Выбор пи-алгоритма управления и расчет параметров
- •3. Расчет физически реализуемого компенсатора.
- •4. Построение переходного процесса в системе по задающему и возмущающему воздействию. Определение показателей качества регулирования.
- •5. Непосредственное цифровое управление (нцу).
- •6. Построение сау с использованием методов нечёткой логики
- •Расчёт управляющего воздействия нечёткого регулятора
- •Заключение
- •Список используемой литературы
- •Приложение 1
- •Приложение 2
- •Приложение 3
1. Получение математической модели объекта в виде передаточной функции.
Согласно заданным в таблице 1 экспериментальным точкам строится экспериментальная характеристика переходного процесса. Исследуемый объект – двухканальный (канал: u-y и канал: f-y) по обоим каналам регулирования является объектом с самовыравниванием (рис.2). Объекты с самовыравниванием аппроксимируют передаточными функциями с введением звена запаздывания.
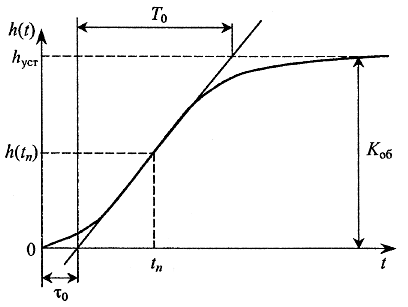
Рис. 2. Переходная характеристика ОУ с самовыравниванием

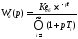 , (1.1)
, (1.1)
где:
Коб – коэффициент передачи;
- время запаздывания;
То – постоянная времени.
Простейшим частным случаем оператора (1.1), имеющим в инженерной практике наибольшее применение, является передаточная функция вида:
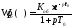 . (1.2)
. (1.2)
1.Для определения параметров объекта по управляющему каналу проведём касательную к экспериментальной переходной характеристике в точке перегиба, которая имеет координаты (tп; h(tп)). Далее определяем параметры передаточной функции по управляющему каналу (приложение 1, рис.1):
Канал u-y
kоб= hуст=0,64 ;о= 3,3 с; То= 6,3 с; h(tп) = 0,18; tп= 5 с;
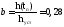 .
.
Для нахождения математической модели объекта воспользуемся различными методами аппроксимации.
Модель 2
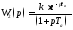 (1.2)
(1.2)
Определяем коэффициенты:
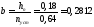
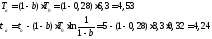
Подставив числовые значения в формулу (1.2)
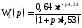
Модель 4
Модель определим методом Лукаса, представленным в литературе [1].
|
|
(1.3) |
Определим коэффициенты:
постоянная
времени:
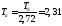 с;
с;
время
запаздывания:
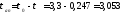 с.
с.
Подставив числовые значения в формулу (1.3) получим четвёртую математическую модель объекта управления (рис.1, кривая 4):

Модель 6
Модель получим
методом Ротача, представленным в
литературе [4]. Задача математического
описания в этом случае заключается в
поиске таких Та1, Та2и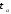 ,
при которых кривая (рис.1, кривая 6)
максимально приближается к истинной
экспериментальной кривой. Для упрощения
расчётов, в литературе предложена
номограмма (рис 3).
,
при которых кривая (рис.1, кривая 6)
максимально приближается к истинной
экспериментальной кривой. Для упрощения
расчётов, в литературе предложена
номограмма (рис 3).
|
|
(1.5) |
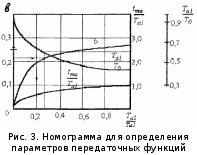
По номограмме (рис.3.) можно найти
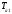 ,
, по известным
по известным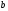 и
и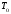 .
По известному значению
.
По известному значению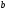 =0,28
=0,28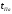 =5,
т.кb>0,265 проводим
дополнительную касательную, для которой
=5,
т.кb>0,265 проводим
дополнительную касательную, для которой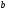 =0,125
находим значение
=0,125
находим значение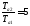 ,
после чего определяем
,
после чего определяем ,
,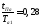 и, следовательно:
и, следовательно:
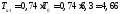
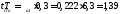
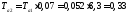
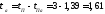
Подставив числовые значения в формулу (1.5), получим шестую математическую модель:
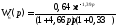
Модель 7
Модель определим методом Лукаса, представленным в литературе [1].
|
|
(1.6) |
Определим коэффициенты передаточной функции:
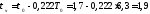 с.
с.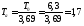 с.
с.
Подставив числовые значения в формулу (1.6), получим седьмую математическую модель (кривая 7):

Погрешность аппроксимации
Вычислим погрешности аппроксимации полученных передаточных функций по интегральному критерию по формуле:
|
|
(1.4) |
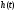 -
аппроксимирующая переходная характеристика;
-
аппроксимирующая переходная характеристика;
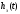 -
заданная переходная характеристика.
-
заданная переходная характеристика.
Для этого найдем площадь под заданной переходной характеристикой и площади расхождения исходной и каждой из полученных переходных характеристик (рис.1). Погрешность определим как отношение этих площадей:
Для кривой 2
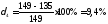
Для кривой 4
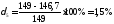
Для кривой 6
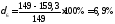
Для кривой 7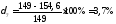
В качестве окончательной выбираем передаточную функцию ОУ, имеющую наименьшую погрешность аппроксимации:
|
Канал u-y 2. Проделаем все описанное выше для возмущающего канала (см. пункт 1) (параметры передаточной функции определим по рис.2, приложение 1) kоб= hуст=1,3 ;о= 1,7 с; То= 4,2 с;
Для нахождения математической модели объекта воспользуемся различными методами аппроксимации.
Определяем коэффициенты:
Подставив числовые значения в формулу (1.2)
Модель 4 постоянная
времени:
время
запаздывания:
|

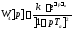
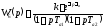
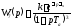
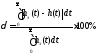 ,
где:
,
где:
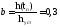 .
.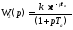 (1.2)
(1.2)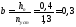
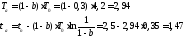
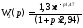
 с;
с;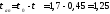 с.
с.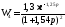 (кривая 4, рис.2)
(кривая 4, рис.2)