6.1.5. Расчет переходных процессов в цепях с одним накопителем энергии - емкостью

Электромагнитные процессы при переходном процессе в таких цепях обусловлены запасом электрической энергии в емкости С и рассеиванием этой энергии в виде тепла на активных сопротивлениях цепи. При составлении дифференциального уравнения следует в качестве неизвестной функции выбрать напряжениеu_Cна емкости. Следует отметить, что при расчете установившихся режимов, т. е. при определении начальных условий и принужденной составляющей, сопротивление емкости в цепях постоянного тока равно бесконечности.

Пример 6.2.Включение последовательной цепиR,Cна постоянное напряжение.

Цепь (рис. 6.3, а), состоящая из последовательно соединенных сопротивленияR= 1000 Ом и емкостиС= 200 мкФ, в некоторый момент времени подключается к постоянному напряжениюU=60 В. Требуется определить ток и напряжение емкости в переходном процессе и построить графикиu_C (t), i(t).

а б в

R i R i, A u, B

60

0.06

U C U C t = 0.02,c

i

0 t 2t 3t t, с

Рис. 6.3

Решение. 1.Определяем начальные условия. Начальное условиеu_C (-0) = 0, так как цепь до коммутации была отключена (полагаем достаточно длительное время).

2.Изображаем электрическую цепь после коммутации (рис. 6.3,б), указываем направления тока и напряжений и для нее составляем уравнение по второму закону Кирхгофа

или .

3.Преобразуем уравнение п.2 в дифференциальное. Для этого, подставив вместо токаiизвестное уравнение, получим:

4.Решение уравнения (искомое напряжение на емкости) ищем в виде:

.

5.Определяем. Так как в цепи постоянного тока в установившемся режиме сопротивление емкости равно бесконечности (при этом), то все напряжение будет приложено к емкости. Поэтому

u_Cпр=U=60 В.

6.Составляем однородное дифференциальное уравнение

решением которого будет функция

7.Составляем характеристическое уравнениеRCl+ 1= 0, корень которого равен

Постоянная времени

8.Запишем решение.

9.Согласно второму закону коммутации и начальным условиям

10.Определим постоянную интегрированияАпутем подстановкиt=0 в уравнение п.8

Напряжение на емкости в переходном процессе

В.

11.Ток в цепи можно определить по уравнению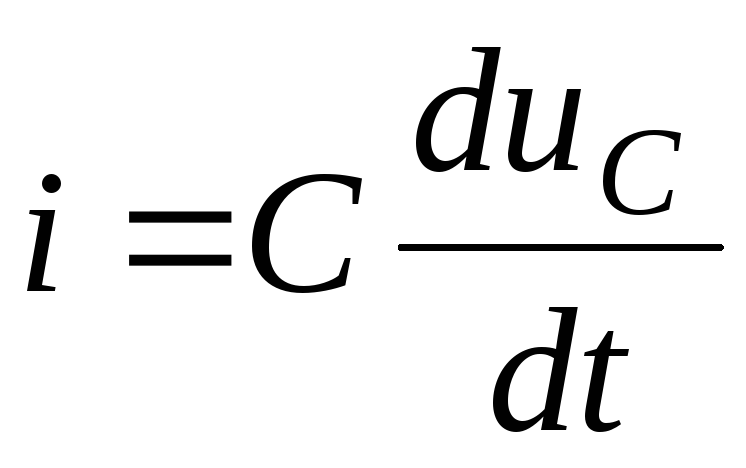

или по уравнению п. 2

Графики u_C (t) иi(t) представлены на рис. 6.3,в.

6.1.6. Метод переменных состояния

Мгновенные значения токов и напряжения, определяющие энергетическое состояние электрической цепи, называются в данном методе переменными, а сам метод назван методом переменных состояния.

Этот метод основан на составлении системы дифференциальных уравнений и, как правило, численном их решении с помощью ЭВМ.

В качестве неизвестных здесь следует принимать переменные, которые не имеют разрывов, т.е. за время не должно быть скачкообразного изменения этих величин. Такими переменными, следовательно, должны быть токiи потокосцеплениев индуктивности, напряжениеи зарядна емкости. В противном случае при численном решении производных в точках, где имеется разрыв, возникает бесконечно большая величина, что недопустимо.

Существуют различные численные методы расчета дифференциальных уравнений. Это методы Эйлера, Рунге-Кутта и другие, которые отличаются друг от друга точностью расчета, объемом и временем вычислений. При этом, чем больше точность вычислений, тем больше требуется времени для решения.

Расчет методом переменных состояния рекомендуется вести в следующей последовательности:

1. Определить начальные условия.

2. Составить систему дифференциальных уравнений.

3. Все переменные в уравнениях п.2 выразить через токи или потокосцепленияв индуктивностях и напряженияили зарядына емкостях.

4. Все уравнения п.3 свести к нормальной форме Коши.