6.1.4. Расчет переходных процессов в цепях с одним накопителем энергии - индуктивностью

Электромагнитные процессы при переходном процессе в таких цепях обусловлены запасом магнитной энергии в индуктивности и ее рассеиванием в виде тепла на активных сопротивлениях. Отметим, что цепи, содержащие всего один участок с накопителем магнитной энергии (L), описываются дифференциальным уравнением первого порядка, т.е. такие уравнения содержат только одну производную.

При расчете установившегося режима в случае постоянных внешних ЭДС необходимо помнить, что сопротивление индуктивности постоянному току равно нулю.

Ниже рассмотрим пример. Расчет его выполнен по алгоритму, который рекомендуется к применению для других подобных задач.

Пример 6.1. Включение последовательной цепи R, L на постоянное напряжение

Последовательная цепь R,L(рис. 6.2,а)R =100 Ом иL=2 Гн подключается к постоянному напряжениюU =100 В. Требуется определить ток и напряжение на индуктивности в переходном процессе и построить графики зависимостейi_L(t), u _L(t).

Решение.

1.Определяем начальное условие:, так как цепь до коммутации была отключена (принимаем, что это было достаточно длительное время).

2.Изображаем электрическую цепь после коммутации (рис. 6.2,б) и на ней указываем направления токов и напряжений.

3.Для схемы (рис. 6.2,б) составляем уравнение по второму закону Кирхгофа:

. (6.7)

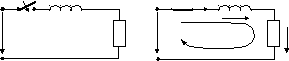а б i L

L u_L

U R U R u_R

Рис. 6.2

Подставляя уравнения элементов в уравнение (6.7) и учитывая,

что для последовательной цепи , получим:

(6.8)

Уравнение (6.8) – линейное дифференциальное уравнение первого порядка.

4.Решение уравнения (искомый ток переходного процесса) ищем в виде

(6.9)5.Определяемi_пр, который представляет собой установившийся постоянный ток в цепи. Находим его по закону Ома, учитывая при этом, что индуктивное сопротивление при постоянном токе равно нулю:

А.

6.Составляем однородное дифференциальное уравнение

решением которого будет функция

7.Составляем характеристическое уравнение для определения

корень, которого равен

Величина называется постоянной времени цепи и имеет размерность времени.

8.Запишем решение (ток в переходном процессе)

(6.10)

9.Согласно первому закону коммутации и начальным условиям

10.Определим постоянную интегрированияАпутем подстановки в уравнение (6.10)t= 0 и, учитывая условие п. 9, получим

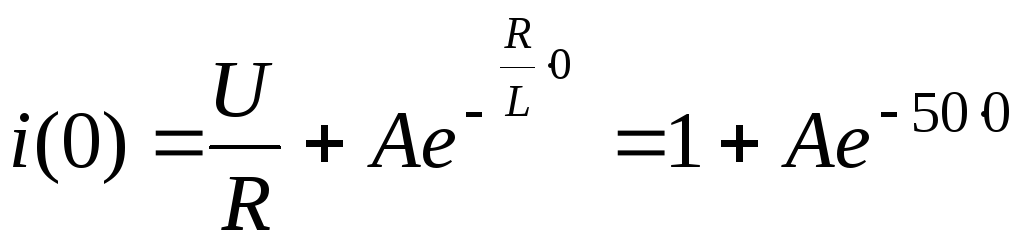; ; A= –1.

Ток в переходном процессе

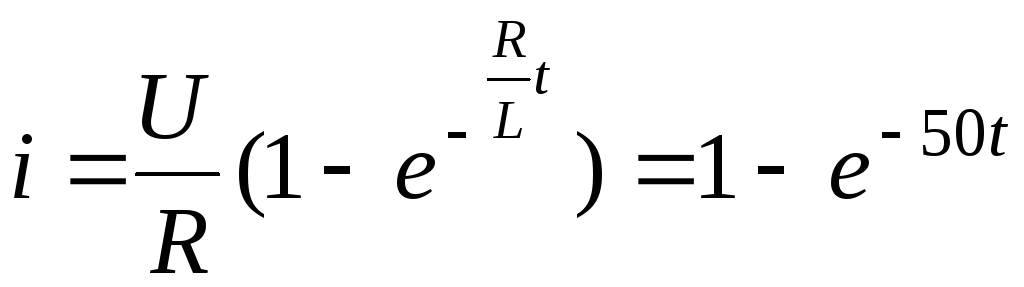А. (6.11)

11.Напряжение на индуктивности можно определить по уравнению

В.

Постоянную времени tможно определить графически. Для этого к любой точке функциипроводят касательную, тогда длина подкасательной на оси времени даст в том же масштабе, что и время, постоянную времениt. За длительность переходного процесса принимают время, равное. За это время величина тока в переходном процессе будет отличаться от установившегося значения тока менее чем на 1 %.