
- •Введение
- •Глава 1. Ряды фурье
- •§ 1. Векторные пространства
- •§ 2. Скалярное произведение и норма функций
- •§ 3. Ортогональные системы функций. Коэффициенты Фурье. Ряд Фурье
- •§ 4. Сходимость в среднем. Равенства Парсеваля
- •§ 5. Тригонометрический ряд Фурье на промежутке [–l, l]
- •§ 6. Сходимость тригонометрического ряда Фурье. Теорема Дирихле
- •§ 7. Разложение в тригонометрические ряды четных и нечетных функций
- •§ 8. Ряд Фурье для функции, заданной на промежутке [0, l]
- •§ 9. Ряды Фурье для комплексных функций
- •§ 10. Комплексная форма тригонометрического ряда Фурье
- •Глава 2. Интеграл фурье
- •§ 11. Сходимость интеграла Фурье
- •§ 12. Преобразование Фурье
- •§ 13. Основные сведения из теории преобразования Фурье
- •Глава 3. Операционное исчисление
- •§ 14. Преобразование Лапласа
- •§ 15. Изображения простейших функций
- •§ 16. Основные теоремы операционного исчисления
- •§ 17. Формула разложения Хевисайда
- •§ 18. Операторный метод решения дифференциальных уравнений
- •§ 19. Приложения
- •Примеры для самостоятельного решения
- •Оглавление
Примеры для самостоятельного решения
Задание 1. Разложить в ряд Фурье функции, заданные на интервале –, :
1.![]()
![]() 2.
2.![]()
3.![]() .
4.
.
4.![]() .
.
5.![]() 6.
6.![]()
7.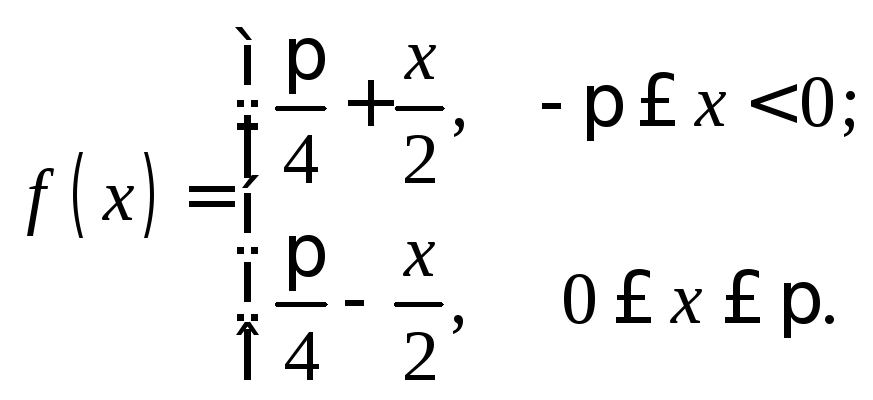 8.
8.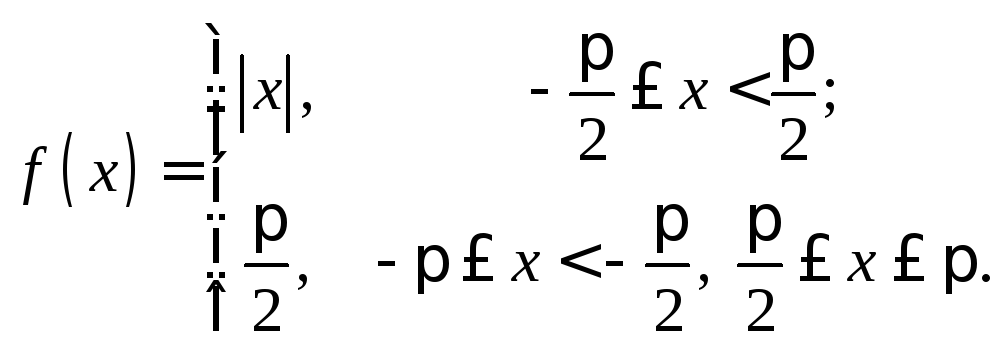
9.
10.
11.
![]() 12.
12.![]()
13.
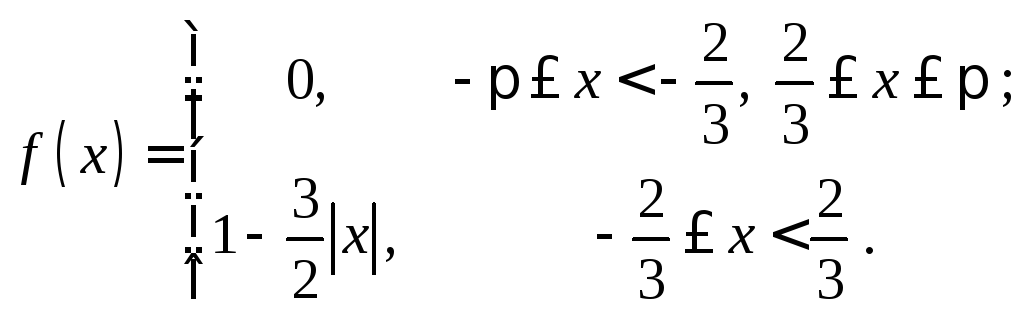 14.
14.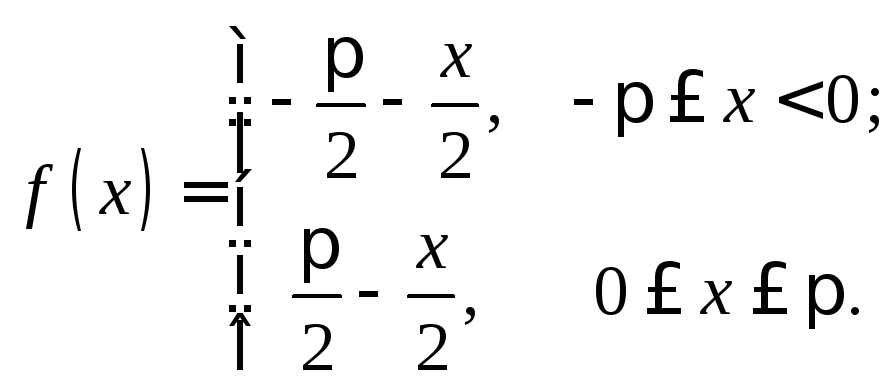
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.![]() 20.
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.![]() 26.
26.![]()
27.
![]() 28.
28.![]()
29.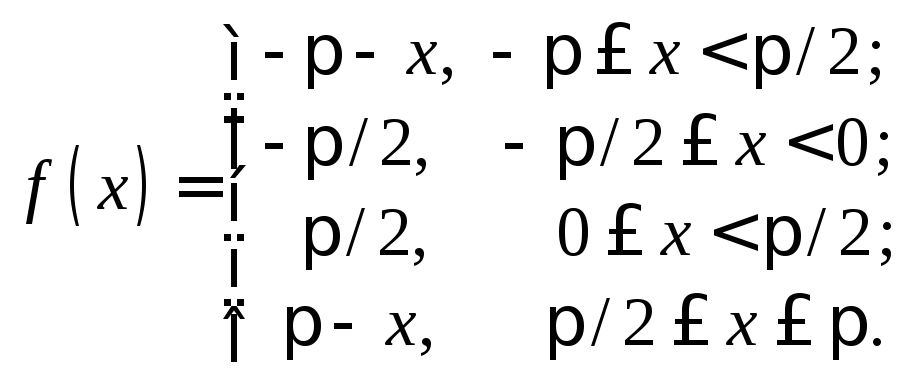 30.
30.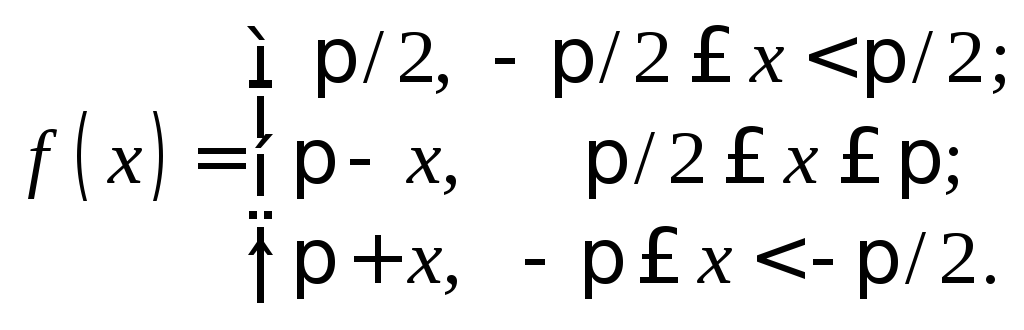
31.
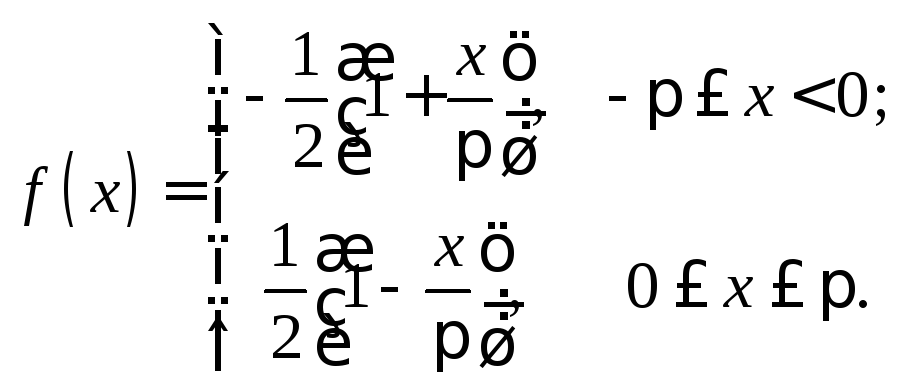
Задание 2. Разложить
в ряд Фурье функции, заданные на интервале
![]() :
:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.![]()
7.
![]() 8.
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.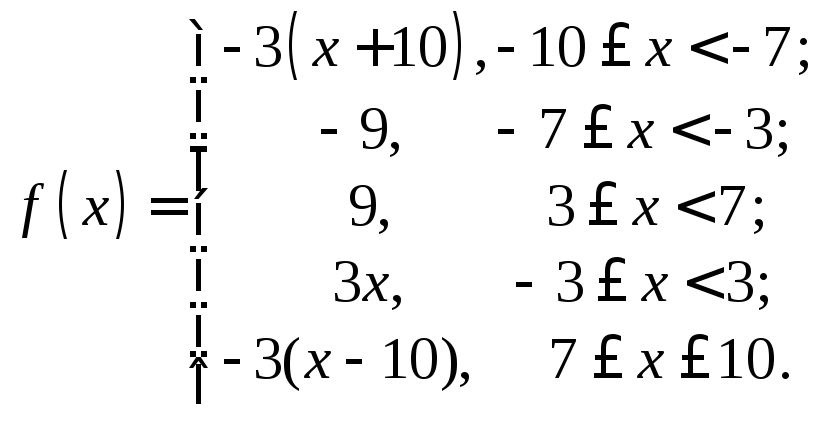 14.
14.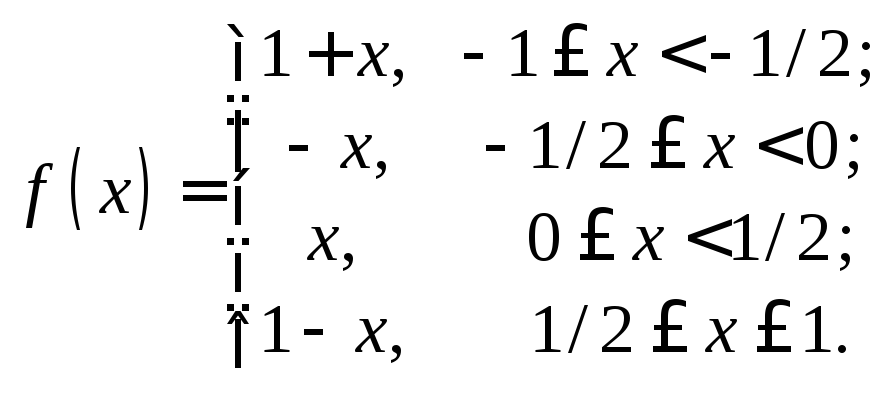
15.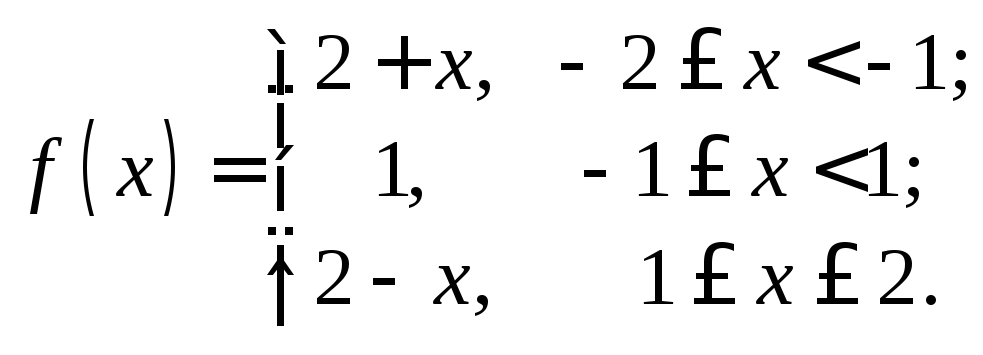 16.
16.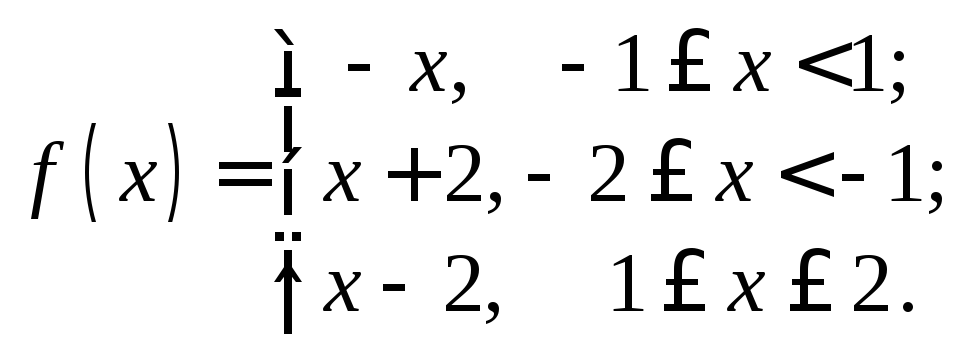
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
25.![]() 26.
26.
![]()
27.
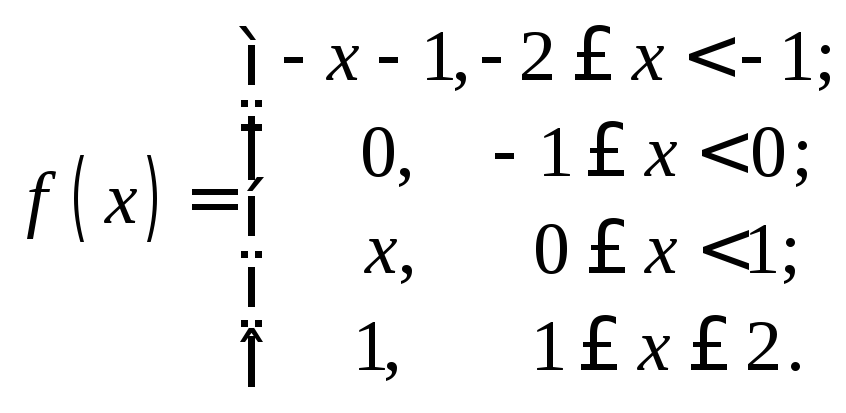 28.
28.
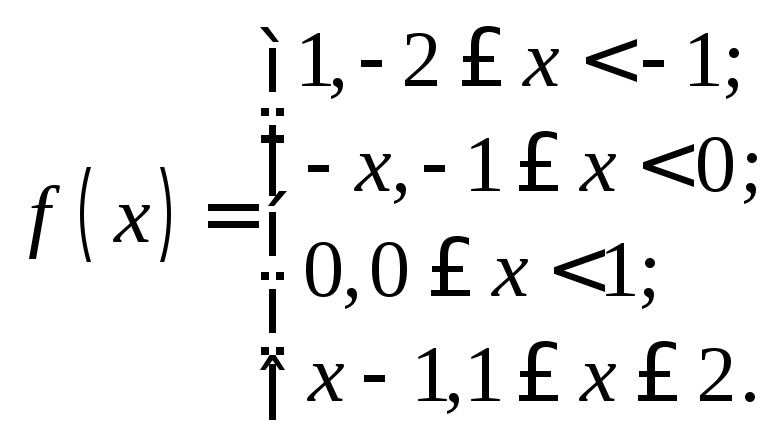
29
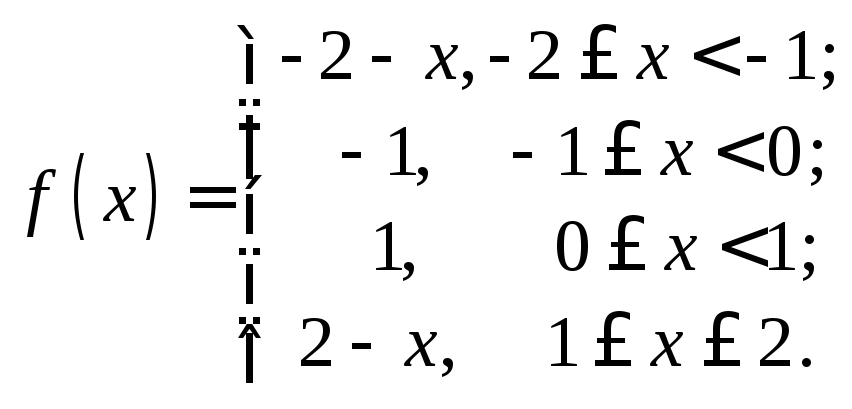 30.
30.
![]() =
=![]()
Указание. Для решения примера 15 воспользоваться формулами 6
![]()
![]()
Задание 3. Представить интегралом Фурье следующие функции:
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.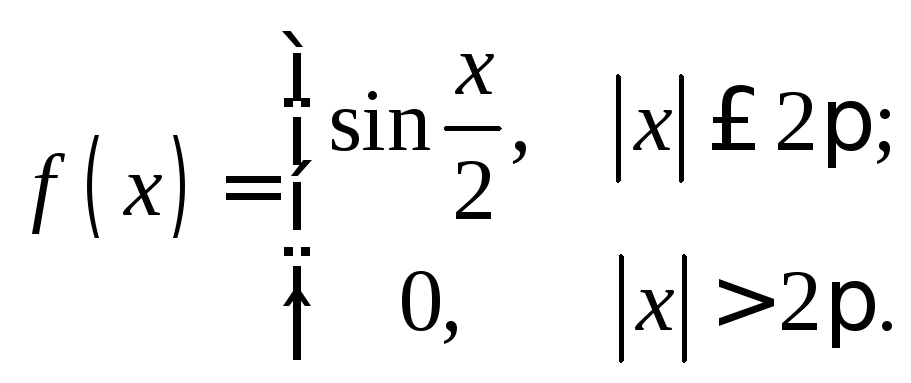
13.![]() .
14.
.
14.![]() .
15.
.
15.![]() .
.
16.![]() .
17.
.
17.![]() .
18.
.
18.![]() .
.
Указание. При решении следует воспользоваться формулами
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]() ;
;![]()
![]() .
.
Задание 4. Найти
косинус-преобразование Фурье
![]() следующих функций:
следующих функций:
1.![]() 2.
2.![]() .
3.
.
3.![]() .
.
4.![]() .
5.
.
5.![]() .
.
Задание 5. Найти
синус-преобразование Фурье
![]() следующих функций:
следующих функций:
1.
![]() 2.
2.![]()
3.![]() 4.
4.![]() .
.
5.
![]() .
6.
.
6.![]() .
7.
.
7.![]() .
.
Ответы
Задание 1
1. ![]() .
2.
.
2.![]() .
.
3.
![]() .
4.
.
4.
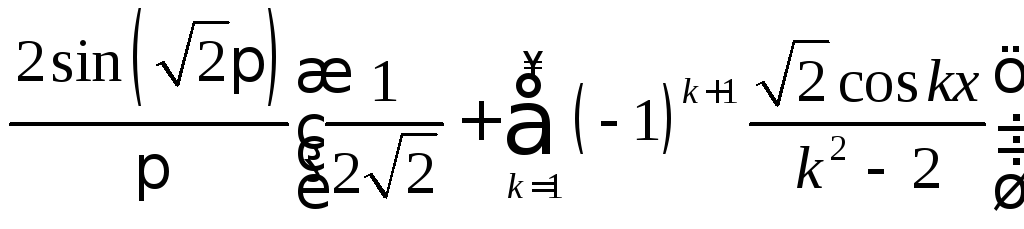 .
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
 .
.
13.
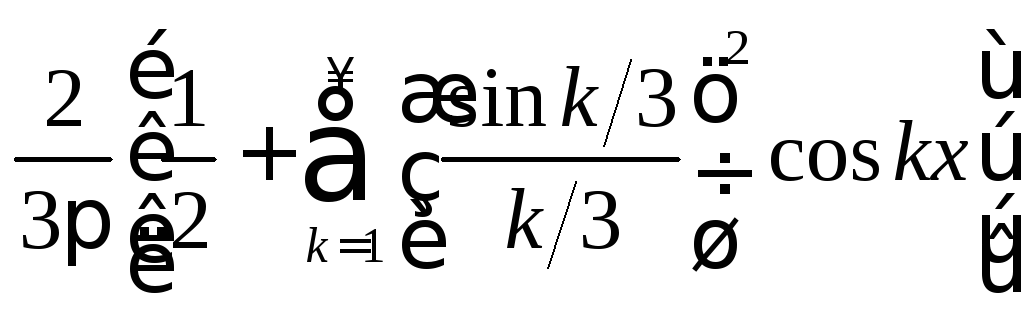 .
14.
.
14.
![]() .
.
15.
![]() .
16.
.
16.
![]() .
.
17.
![]() .
18.
.
18.![]() .
.
19.
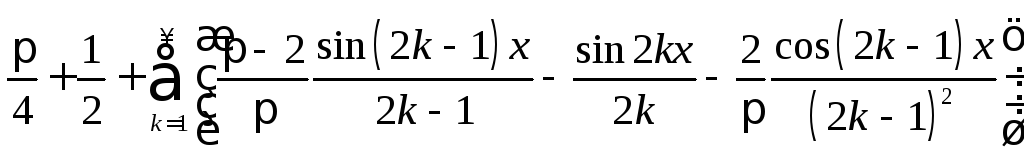 .
.
20.
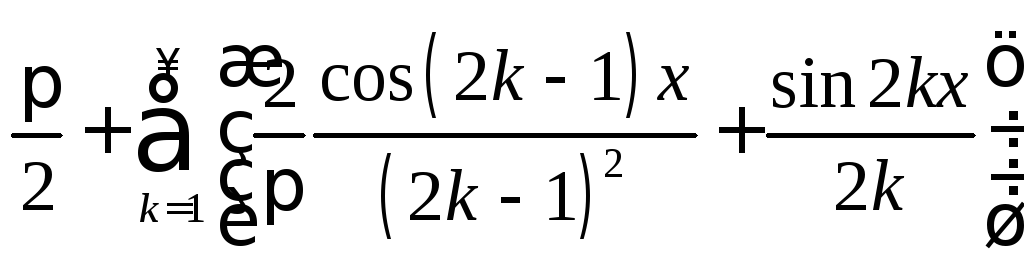 .
.
21.
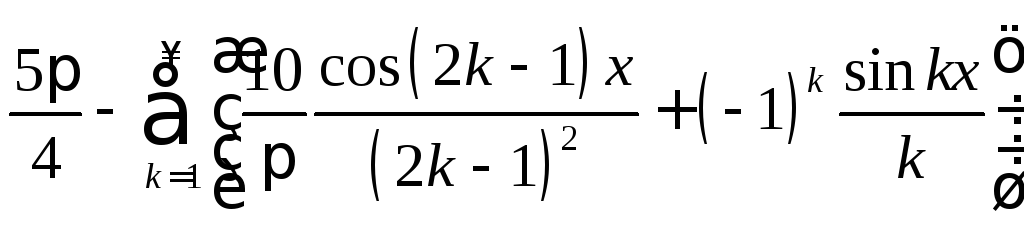 .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
25.
.
25.
![]() .
.
26.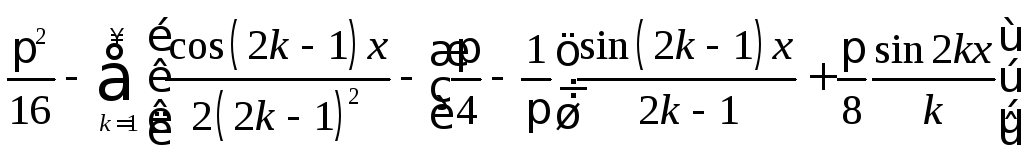 .
.
27.
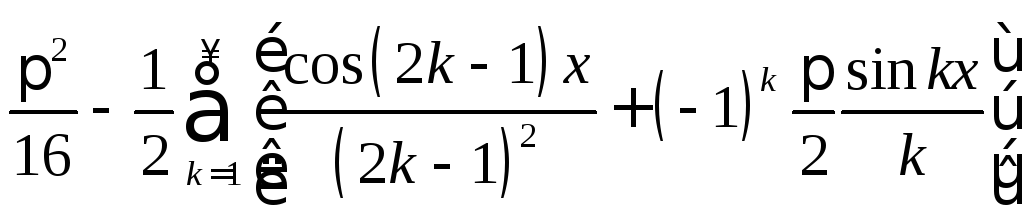 .
.
28.
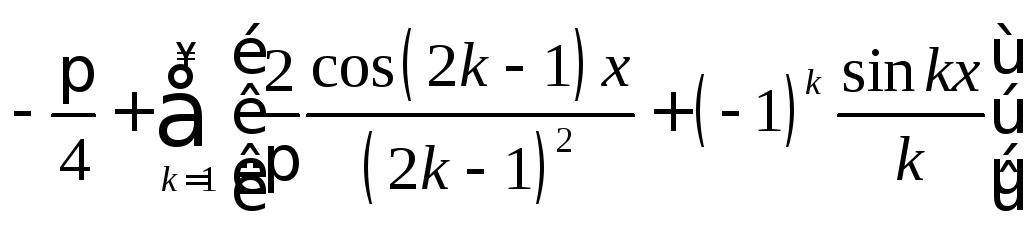 .
.
29.
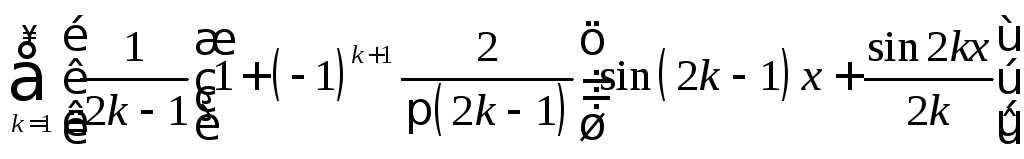 .
.
30.
![]() .
.
31.
![]() .
.
Задание 2
![]() .
.
2.
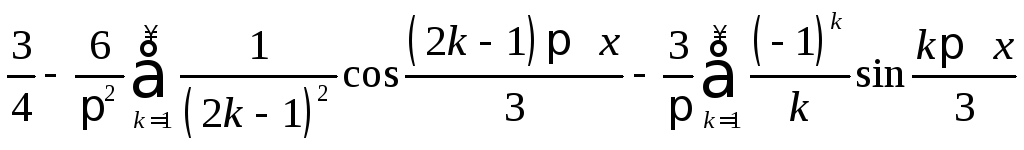 .
.
3.
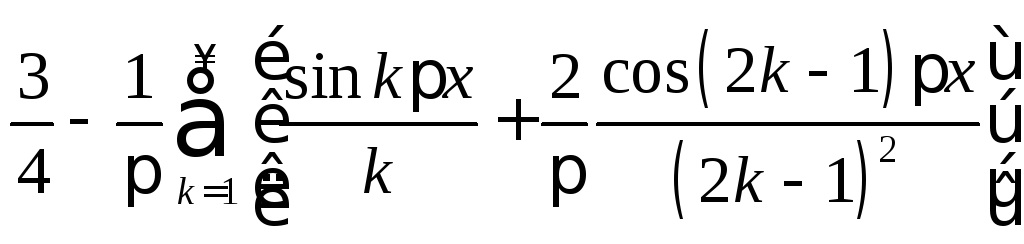 .
.
4.
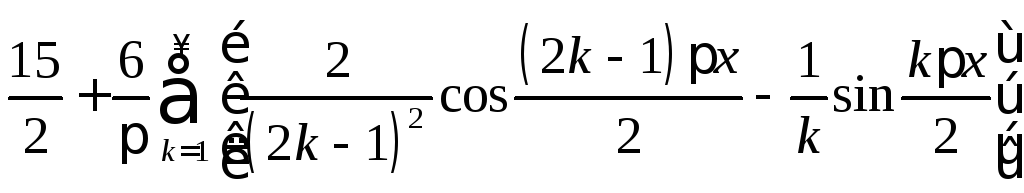 .
.
5.
![]() .
6.
.
6.
![]() .
7.
.
7.![]() .
.
8.
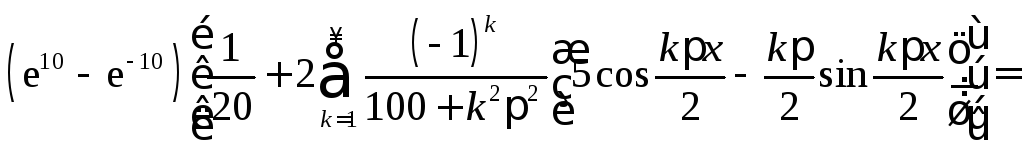
 .
.
9.
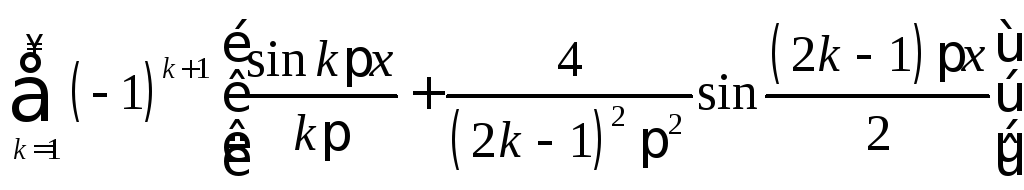 .
.
10.
![]() .
11.
.
11.![]() .
.
12.
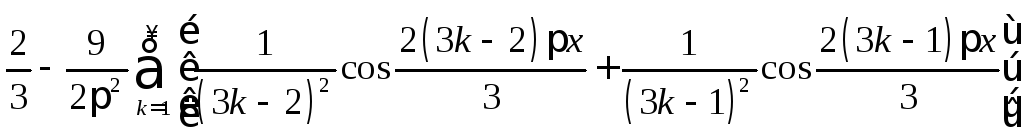 .
.
13.
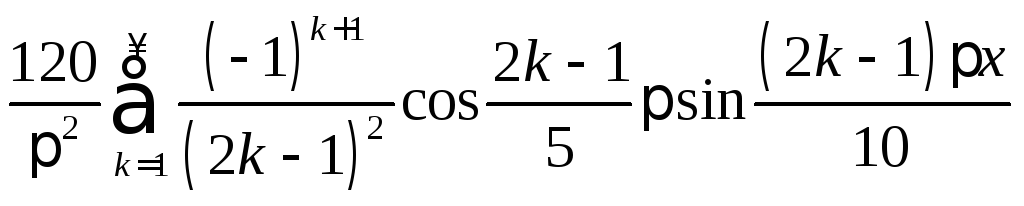 .
.
14.
![]() .
.
15.
![]() .
.
16.
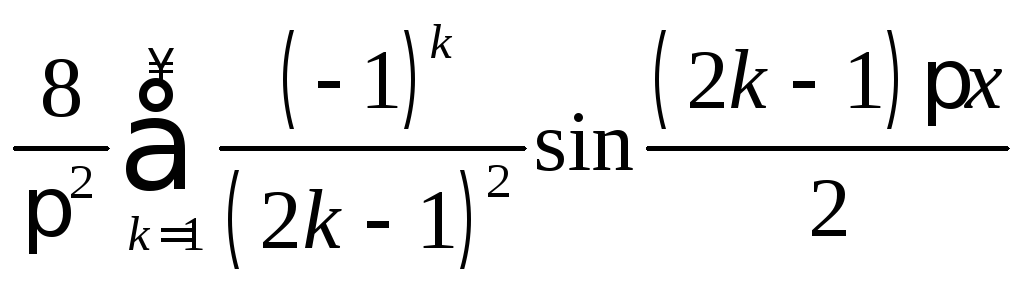 .
17.
.
17.
![]()
18.
![]() .
19.
.
19.![]() .
.
20.
![]() .
.
21.
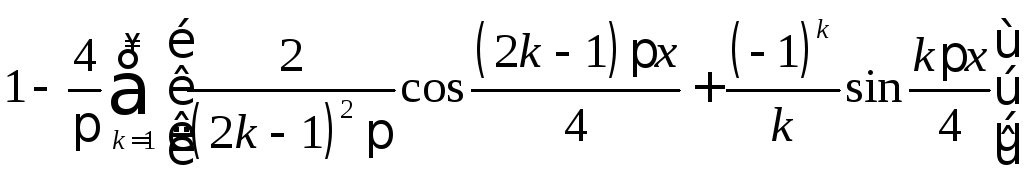 .
.
22.
![]() .
23.
.
23.
![]() .
.
24.
![]() .
25.
.
25.
![]() .
.
26.
![]() .
.
27.
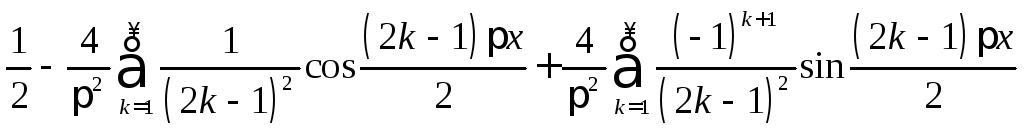 .
.
28.
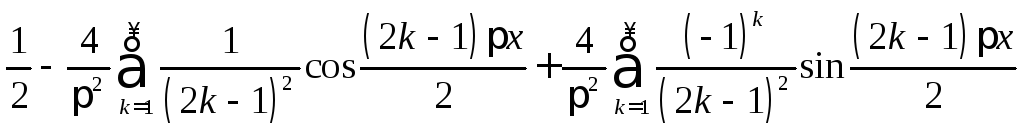 .
.
29.
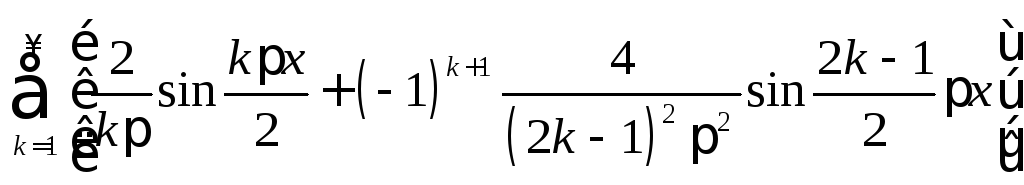 .
.
30.
![]() .
.
Задание 3
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
7.
.
7.![]() .
.
8.
![]() .
9.
.
9.![]() .
10.
.
10.![]() .
.
11.
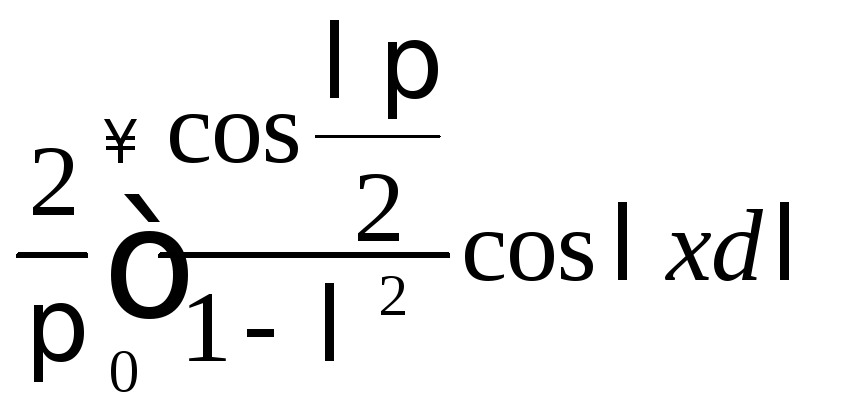 .
12.
.
12.![]() .
13.
.
13.![]() .
.
14.
![]() .
15.
.
15.
![]() .
16.
.
16.
![]() .
.
17.
![]() .
18.
.
18.
![]() .
.
Задание 4
1.
![]() .
2.
.
2.![]() .
.
3.
![]() .
4.
.
4.![]() .
5.
.
5.![]() .
.
Задание 5
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.![]() .
7.
.
7.![]() .
.
Рекомендательный библиографический список
Основной:
1. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1972.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления. Часть II. М.: Наука, 1985.
3. Шипачев В.С. Высшая математика. М.: Высшая школа, 1998.
Дополнительный:
4. Данко П.В. Высшая математика в упражнениях и задачах / П.В.Данко, А.Г.Попов, Г.Н.Кожевникова. М.: Высшая школа, 1997. т.2.
5. Минорский В.П. Сборник задач по высшей математике. М.: Наука, 1987.
6. Прудников А.П. Интегралы и ряды / А.П.Прудников, Ю.А.Брычков, О.И.Маричев. М.: Наука, 1981.
Оглавление
Введение 3
Глава 1. Ряды Фурье 4
§ 1. Векторные пространства 4
§ 2. Скалярное произведение и норма функций 5
§ 3. Ортогональные системы функций. Коэффициенты Фурье. Ряд Фурье 9
§ 4. Сходимость в среднем. Равенства Парсеваля 11
§ 5. Тригонометрический ряд Фурье на промежутке –L, L 15
§ 6. Сходимость тригонометрического ряда Фурье. Теорема Дирихле 16
§ 7. Разложение в тригонометрические ряды четных и нечетных функций 20
§ 8. Ряд Фурье для функции, заданной на промежутке 0, L 22
§ 9. Ряды Фурье для комплексных функций 24
§ 10. Комплексная форма тригонометрического ряда Фурье 29
Глава 2. Интеграл Фурье 32
§ 11. Сходимость интеграла Фурье 32
§ 12. Преобразование Фурье 33
§ 13. Основные сведения из теории преобразования Фурье 40
Глава 3. Операционное исчисление 49
§ 14. Преобразование Лапласа 49
§ 15. Изображения простейших функций 53
§ 16. Основные теоремы операционного исчисления 59
§ 17. Формула разложения Хевисайда 66
§ 18. Операторный метод решения дифференциальных уравнений 70
§ 19. Приложения 79
Примеры для самостоятельного решения 87
Ответы 94
Рекомендательный библиографический список 101
