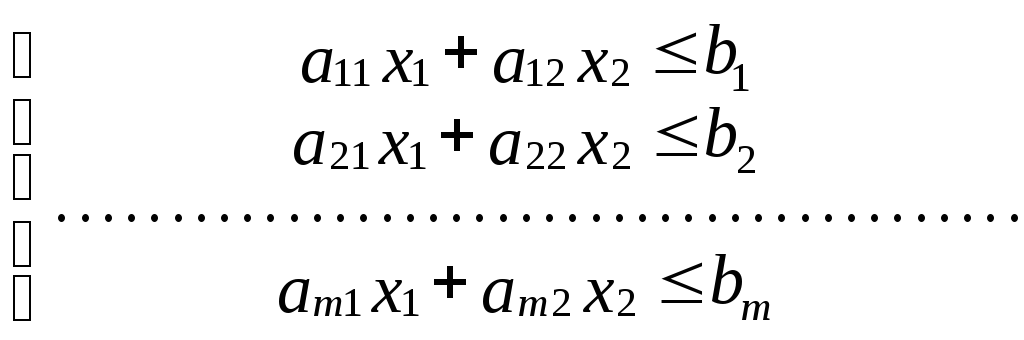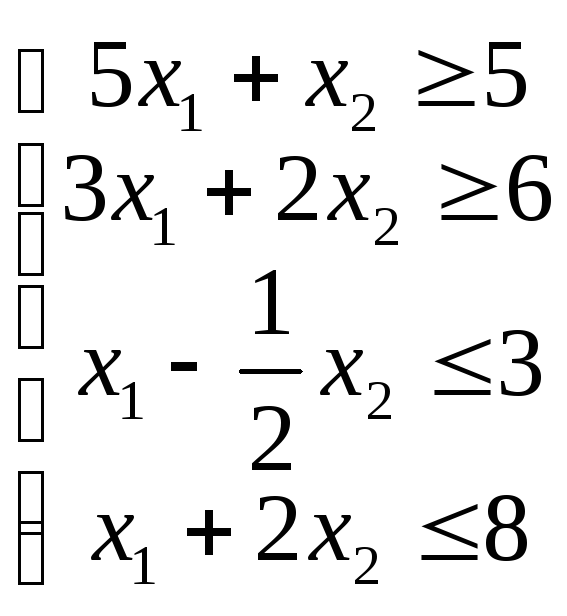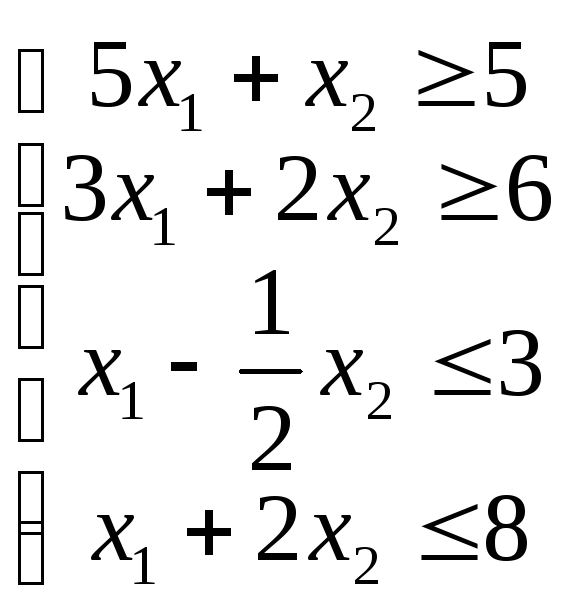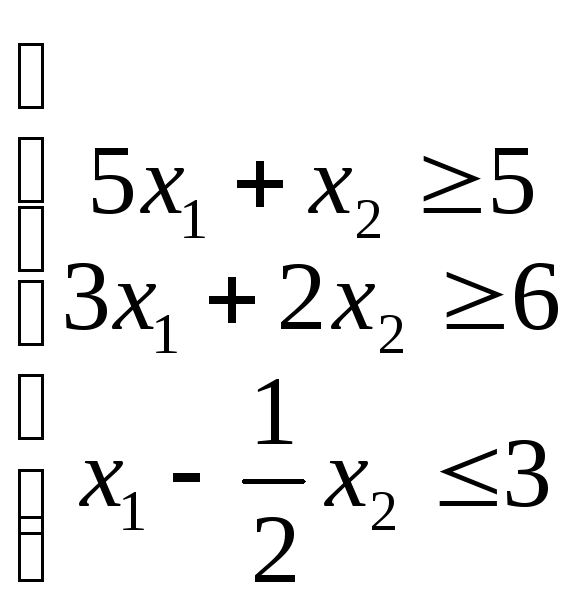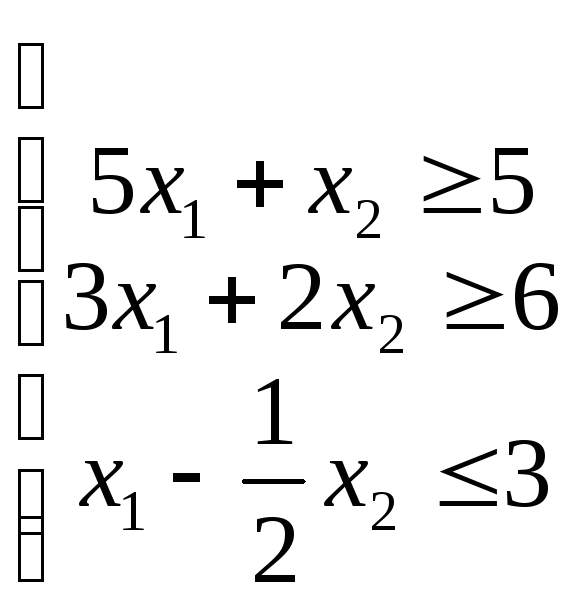1.2. Симплекс-метод

1.2.1. Геометрическая интерпретация

Геометрическое истолкование симплекс-метода наиболее просто может быть проиллюстрировано в случае двух переменных.

Положение 1.

Каждое неравенство с двумя переменнымиx₁иx₂определяет полуплоскость в системе координатx₁0x₂.

Положение 2.

В случае, когда задана система неравенств

(1.10)

то она определяет многоугольную область Dна плоскости, которая является результатом пересеченияm полуплоскостей. ОбластьDназываетсяобластью решенийсистемы неравенств. ОбластьDможет быть ограниченной, неограниченной или пустой. Область решений D обладает важным свойством – она является выпуклой.

Определение 1.Область называется выпуклой, если она вместе с любыми двумя точками содержит весь отрезок их соединяющий.

Определение 2.Прямая называется опорной по отношению к области, если:

1. имеет с областью по крайней мере одну общую точку;

2. вся область лежит по одну сторону от этой прямой.

Положение 3. Пусть задана линейная функция

(1.11)

Для каждой точки плоскости в системе координат x₁0x₂. функцияFпринимает фиксированное значениеF=F₁.

Определение 3. Множество точек, в которых функция двух переменных принимает фиксированное значение, называетсялинией уровня.

Линия уровня для линейной функции – прямая, которая определяется уравнением . ПридаваяF₁различные значения, получим различные линии уровня.

Все линии уровня (для линейной функции) параллельны между собой.

Нормаль к линии уровня определяется через градиент функции. Градиент произвольной функции двух переменных f(x_1,x₂) может быть вычислен по формуле

,

(1.12)

поэтому градиент линейной функции определяется уравнением , т.е. градиент может быть задан вектором, выходящим из начала координат.

Градиент указывает направление наибыстрейшего роста функции в данной точке.

Положение 4.Графическое решение задачи ЛП, определяемой фазовыми ограничениями (1.10), естественными ограничениями и целевой функцией (1.11), основано на мысленном эксперименте по перемещению линии уровня относительнообласти допустимых решений D.Область допустимых решений D задачи ЛП– это множество точек, координаты которых удовлетворяют фазовым и естественным ограничениям. Допустим, множествоDограничено. Пусть при движении прямойF₁в положительном направлении вектораона впервые встретится с многоугольником решений в его вершине, тогда в этом положении прямаяF₁становится опорной, и на этой прямой функцияFпринимает наименьшее значение. При дальнейшем движении в том же направлении прямаяF₁пройдет через другую вершину многоугольника решений (выходя из области решений), и станет также опорной прямой; на ней функцияFпринимает наибольшее значение среди всех значений, принимаемых на многоугольнике решений.

Таким образом, максимизация линейной функции на многоугольнике решений достигается в точке пересечения этого многоугольника с опорными прямыми, перпендикулярными вектору.

Положение 5.Существование решения и количество решений задачи ЛП основано на анализе взаимного расположения области допустимых решенийDи линии уровня.

Если область Dограничена, то возможны два варианта:

А) опорная прямая имеет с многоугольником одну общую точку – одно решение;

Б) опорная прямая параллельна стороне многоугольника (на которой достигается максимум) – множество решений (вся сторона многоугольника).

Если область Dне ограничена, то возможны три варианта:

А) опорная прямая имеет с многоугольником одну общую точку – одно решение;

Б) опорная прямая параллельна стороне многоугольника (на которой достигается максимум) – имеется множество решений;

В) не существует опорной прямой (в направлении роста функции) - множество решений пусто (нет решений).

Пример 2.

Решить графически задачу ЛП (1.13)-(1.15).

	(1.13)
	(1.14)
	(1.15)

Решение

Построим область допустимых решений.

Первое неравенство системы (1.14) задает полуплоскость, границей которой является прямая y₁, определяемая равенством. Построим эту прямую на координатной плоскостиx₁0x₂(рис.1.1), искомой полуплоскостью (она заштрихована) будет, та, которая лежит выше этой прямой.

Второе неравенство задает полуплоскость, границей которой является прямая y₂, определяемая равенством. Также построим прямуюy₂на координатной плоскости и заштрихуем соответствующую полуплоскость.

Аналогично построим полуплоскости, соответствующие неравенствам три и четыре, их границы y₃иy₄, определяются уравнениямиисоответственно.

Пересечение этих четырех плоскостей и плоскостей естественных ограничений определяют область допустимых решений D.

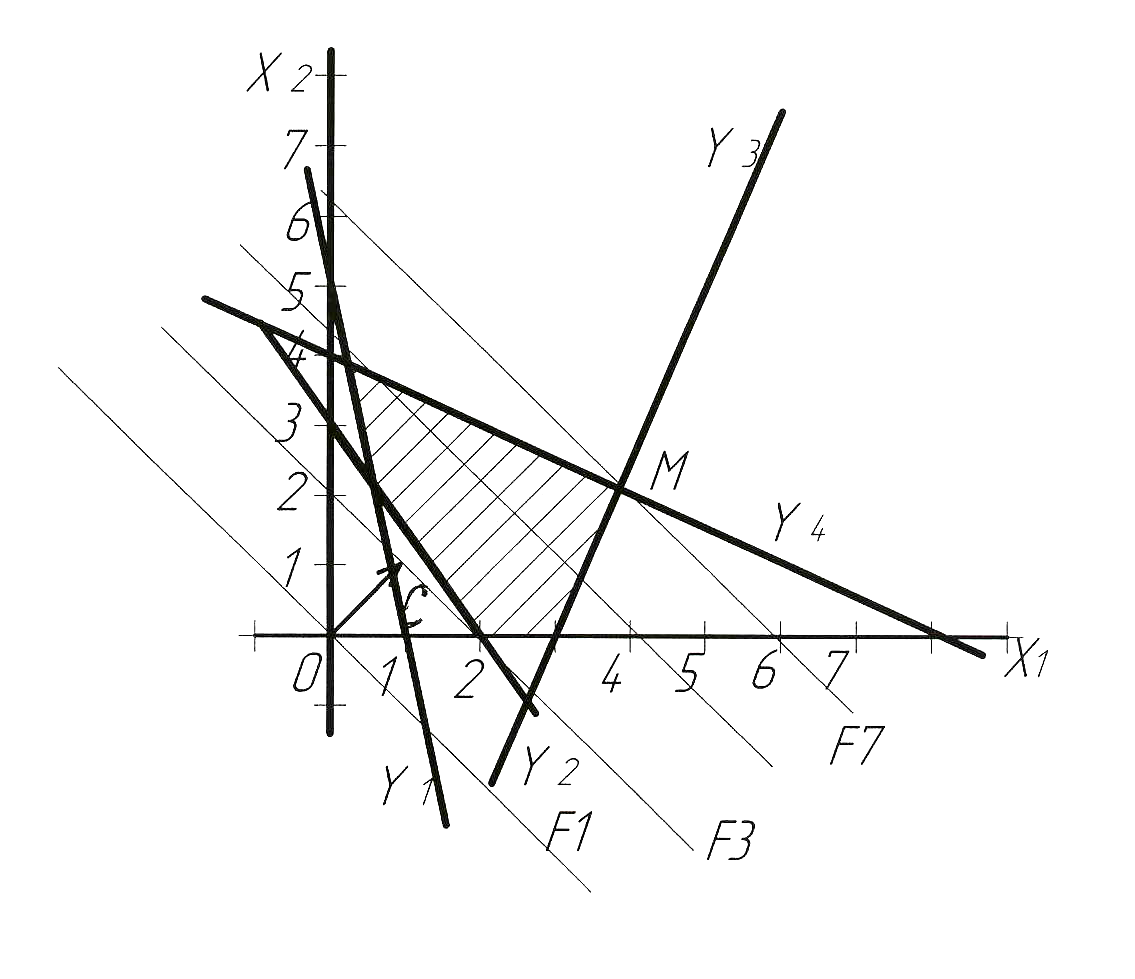
Рис. 1.1

Построим вектор-градиент из начала координат. Проведем линию перпендикулярно вектору. ЛинияF1, проходящая через начало координат, соответствует значению 1, поскольку. Мысленно сдвинем линию уровня в направлении вектора. Первое касание многоугольника Dсоответствует положениюF3. Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Продолжим движение линии уровня до выхода из множестваD. Этому положению соответствует положениеF7. Рассмотрим крайнюю точкуM, которая является точкой пересечения прямыхy₃ иy₄, ее координаты можно определить как решение линейной системы.

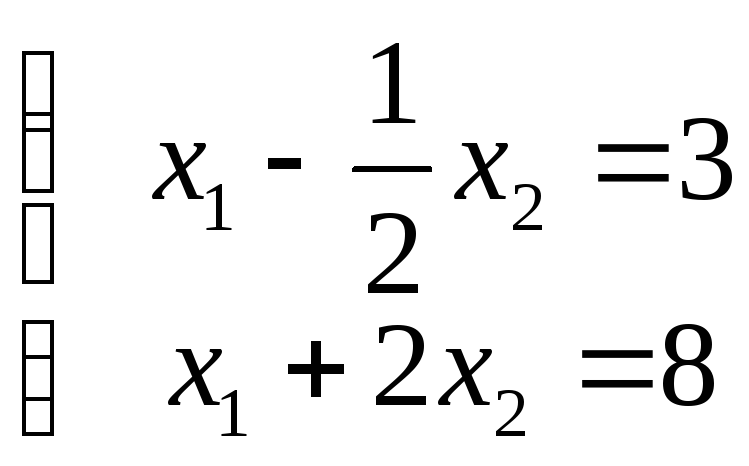
Решением системы является пара чисел x₁=4x₂=2. Этому решению соответствует искомое максимальное значение линейной функции

.

Таким образом, F_max=7 приx₁=4x₂=2.

Вывод.В данном случае линейная функция достигает своего максимального значения в вершине множества решений.

Пример 3.

Решить графически задачу ЛП (1.16) – (1.18).

	(1.16)
	(1.17)
	(1.18)

Решение

Заметим, что система фазовых ограничений (1.17) совпадает с системой (1.14). Поэтому область допустимых решений Dбудет той же самой, что и в примере 2 (рис.1.2).

Построим вектор-градиент из начала координат. Проведем линию перпендикулярно вектору. ЛинияF1, проходящая через начало координат, соответствует значению 1, поскольку. Мысленно сдвинем линию уровня в направлении вектора. Первое касание многоугольника соответствует положениюF3 . Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Продолжим движение линии уровня до выхода из множестваD,. этому положению соответствует положениеF8 . Заметим, что линия уровня параллельна сторонеMN, поэтому решением является множество точек лежащих между крайними точкамиMиN, ТочкаMявляется точкой пересечения прямыхy₃иy₄, ее координаты можно определить как решение линейной системы.

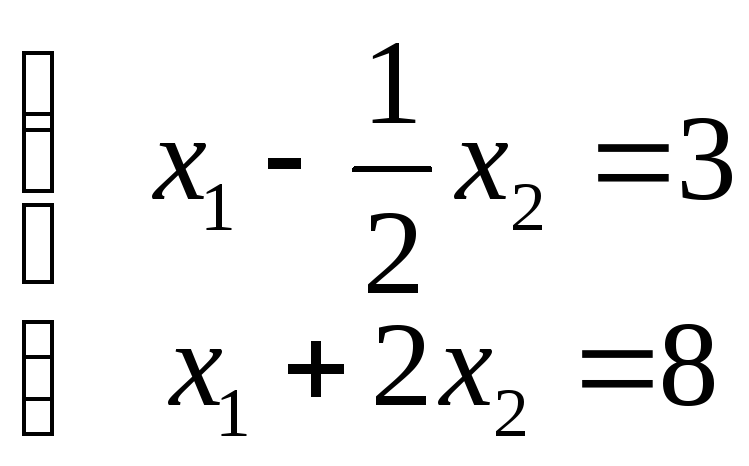
Решением этой системы является пара чисел x₁=4,x₂=2. Эта пара чисел определяет координаты точкиМи в ней достигается искомое максимальное значение линейной функции, равное

.

Таким образом, F_max=9, приx₁=4,x₂=2.

Точка Nявляется точкой пересечения прямыхy₁иy₄; ее координаты можно определить как решение линейной системы

Рис.1.2

Решением полученной системы является пара чисел x₁=2/9,x₂=35/9, которые определяют координаты точкиN, значение целевой функции в которой равно

.

Таким образом, значение в точке Nсовпадает со значением в точкеM.F_max=9, приx₁=2/9,x₂=35/9.

Координаты всех точек, лежащих между MиNможно записать в виде

Значение функции во всех этих точках равно 9.

Вывод.В данном случае линейная функция достигает своего максимального значения во всех точках ребраMNмножества решенийD.

Пример 4.

Решить графически задачу ЛП (1.19) – (1.21).

	(1.19)
	(1.20)
	(1.21)

Решение.

Построим область допустимых решений D(рис. 1.3).

Построение области аналогично примеру 2, но в этом построении отсутствует прямая y₄.

Пересечение трех полуплоскостей с учетом естественных ограничений определяет неограниченную область допустимых решений D.

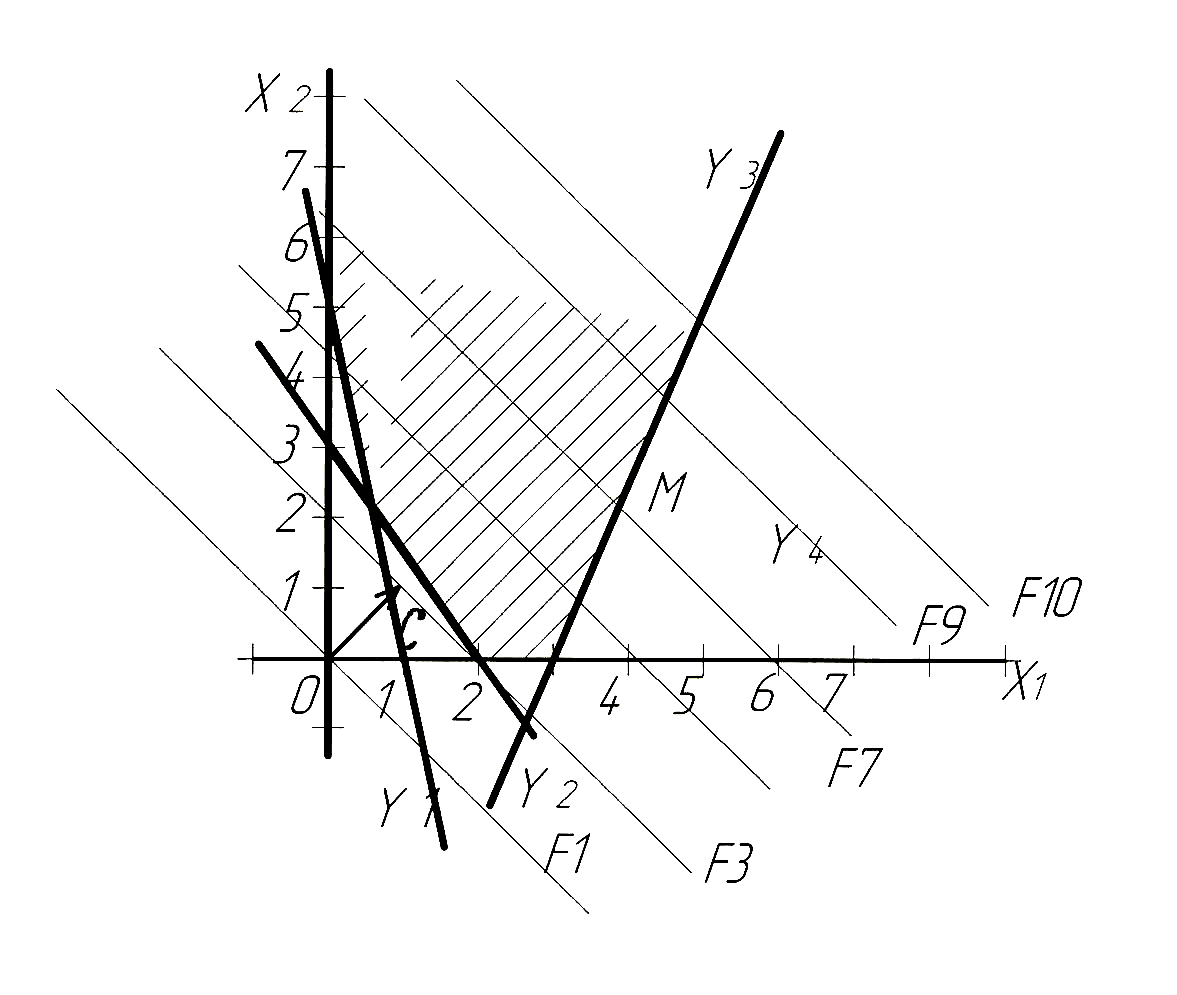
Рис. 1.3

Построим вектор-градиент из начала координат. Проведем линию перпендикулярно вектору–. ЛинияF1, проходящая через начало координат, соответствует значению 1, поскольку.

Мысленно сдвинем линию уровня в направлении вектора . Первое касание многоугольника соответствует положениюF3. Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Заметим, что многогранник незамкнут в направлении роста целевой функции, поэтому целевая функция не имеет максимума. Это объясняется тем, что для любой линии уровня найдется другая линия уровня, лежащая в направлении вектора, которой соответствует большее значение функции.

Вывод.Целевая функция не ограничена, если многогранник незамкнут в направлении роста целевой функции.

Пример 5.

Решить графически задачу ЛП (1.22) – (1.24).

	(1.22)
	(1.23)
	(1.24)

Решение

Построим область допустимых решений D(рис. 1.4), она совпадает с областью в примере 3.

Заметим, что вектор-градиент направлен в противоположную сторону (по сравнению с рис. 1.3). Максимум достигается в единственной точке Р, являющейся точкой пересечения осиx₁ и прямойy₂.

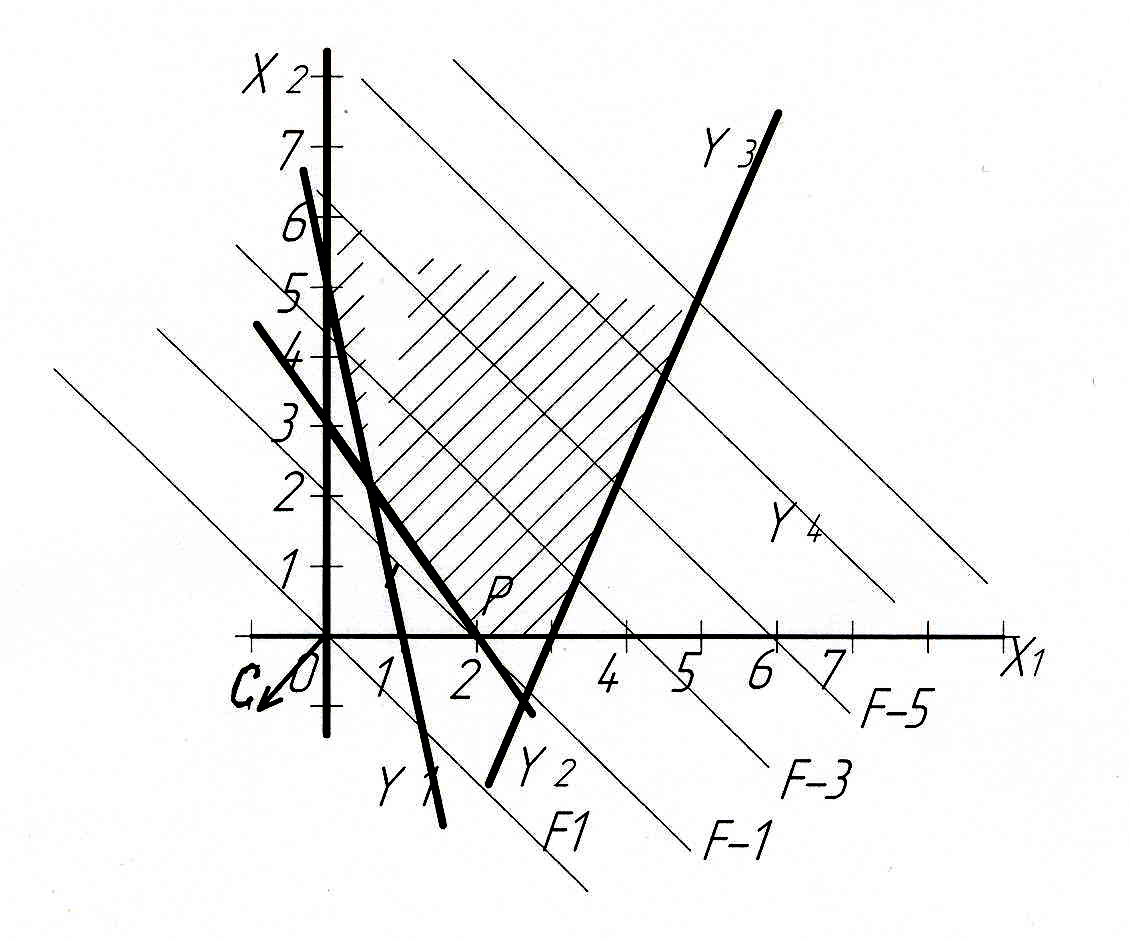
Рис. 1.4

Координаты точки Рможно определить, решив систему уравнений:

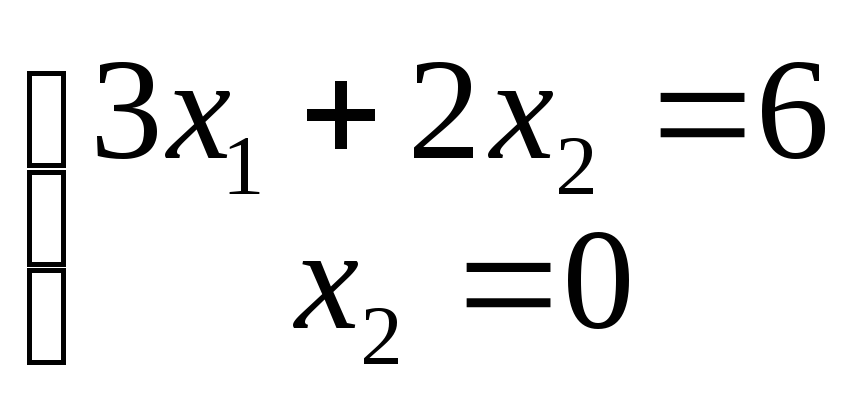
Ее решение x₁=2,x₂=0, значение функции в этой точке равно

Вывод.Задача ЛП имеет решение, когда многогранник замкнут в направлении роста целевой функции.

Рассмотренные примеры иллюстрируют четыре варианта Положения 5.